探析弹簧双振子的运动规律

胡连冬

(湖南省长沙市宁乡市第七高级中学 410635)

弹簧振子的运动问题涉及运动和力的关系、动量能量观念；尤其是“弹簧双振子”运动问题，其运动情况较为复杂，物理情景学生难以想象，即使刚入职的教师面对“弹簧双振子”运动问题也感到束手无策，因此“弹簧双振子”运动问题往往成为历年中学物理竞赛的题型之一.

一、弹簧振子的定义

如图1所示，把轻弹簧的一端固定，另一端连接小球或滑块，当轻弹簧发生形变后，小球或滑块就在平衡位置附近作往复运动，这种现象叫简谐振动，其中弹簧和小球或滑块组成的系统称为弹簧振子.如图2中在轻弹簧的两端各连接一个小球，当弹簧发生形变后，该系统中的两个小球就相对系统的质心作简谐振动，这样的系统称为“弹簧双振子模型”，弹簧振子是一种理想化模型.

二、弹簧振子的运动问题

1.弹簧单振子运动规律

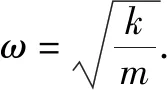
2.弹簧双振子运动规律

(1)弹簧双振子系统质心处于静止状态

例1将原长为l0劲度系数为k的轻弹簧连接A、B两振子，A、B质量分别为m1m2. 将弹簧压缩为l后锁定置于光滑水平面上,如图3所示.当弹簧突然解除锁定后，试分析振子A、B的运动情况.

解析压缩的弹簧解除锁定后，系统在水平方向上不受外力，且系统的总动量为零，根据动量守恒定律可知，系统质心C的速度为零.

把两振子之间的轻弹簧等效为两根原长分别为l10和l20的轻弹簧在质心C处串联，两根轻弹簧对应的劲度系数分别为k1和k2. 这两根轻弹簧的形变量为x1=l10-l1,x2=l20-l2.

整根弹簧的形变量为x=x1+x2,由胡克定律得：

F=k1x1=k2x2=kx

(1)

(2)

结合质心位置分布规律有：m1x1=m2x2

(3)

(4)

(5)

分别求得两振子振动的位移和速度：

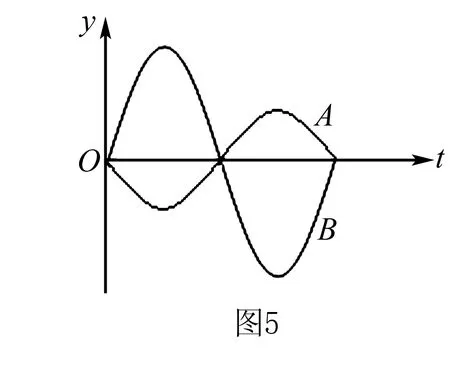
A、B两振子的速度—时间图像如图5所示(振幅不一定相同，由振子质量决定).

(2)弹簧双振子系统质心处于匀速直线运动状态

例2如图6所示，振子AB和轻弹簧连接静止在光滑水平面上，两振子AB质量分别为m1m2，C表示系统的质心位置，现给A一个水平向右大小为V0的初速度，试分析AB两物块的运动情况.

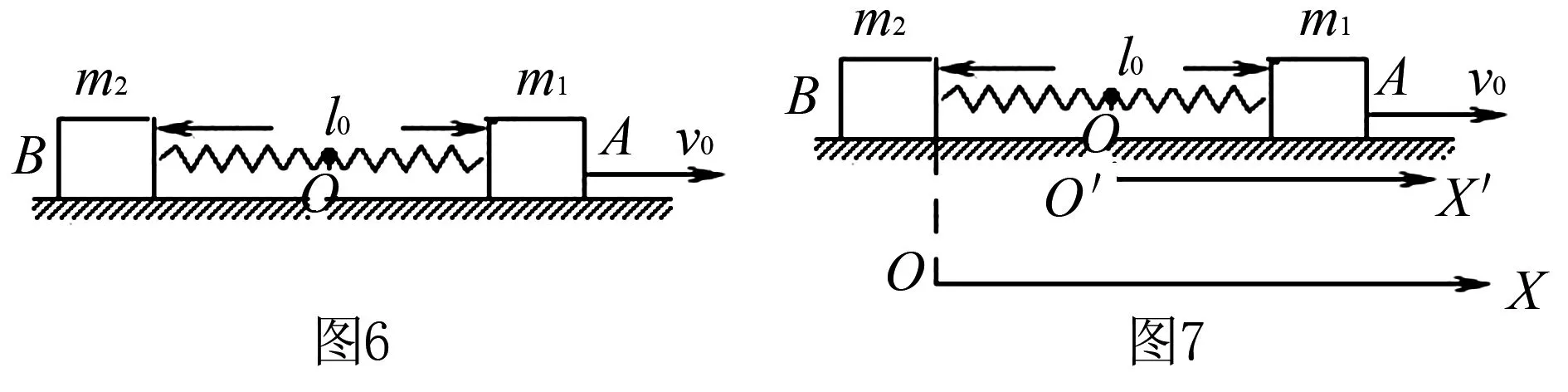
A在质心坐标系O′X′中相对平衡位置的距离xA相=0.

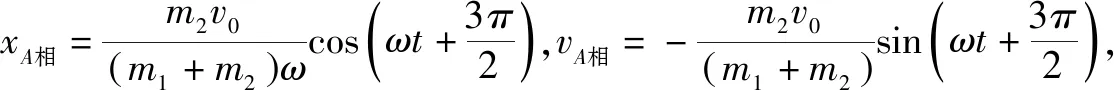
A相对质心C的位置为：

(6)

A相对地面坐标系的速度为：

(7)

在t=0时刻，B物块相对质心C振动的初始条件为：

则B相对质心C的振动方程为：

同理可得B物块在任意时刻t相对质心坐标系o′x′的位置为：

B相对地面参考系ox的位置为：

(8)

B物块相对地面参考系的速度为：

(9)

由(7)(9)两式可作出AB物块在质量m1=m2时相对地面的v-t图像如图8所示.

(3)弹簧双振子系统质心处于匀变速直线运动状态

例3劲度系数为k的轻弹簧，两端系质量为mA和mB的小球A、B，A用细线悬于天花板上，系统处于静止状态.如图9所示，此时弹簧长度为l，现将细线烧断，并以此时为计时起点，试分析任意时刻两小球的运动情况(系统距地面足够高)

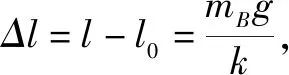
A相对平衡位置的速度v0=0.

由弹簧单振子的振动方程可得A球相对质心的振动方程分别为：

在任意时刻t,A球在质心坐标系o′x′中的位置和速度分别为：

以烧断细线时A所在位置为坐标原点o竖直向下为正方向建立如图10所示的地面参考坐标系ox.则在任意时刻A在ox系中的位置和速度分别为：

同理可得B相对质心的振动方程分别为：

任意时刻B相对质心坐标系o′x′的位置和速度分别为：

因此任意时刻t,B相对地面坐标系ox的位置为：

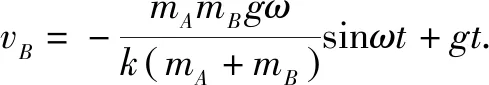
综上所述，弹簧双振子具有相似的运动规律，双振子的运动是振子相对系统质心的简谐振动和系统质心某种运动的合运动.