基于数学建模素养下概率模型的教学设计探究

汪菊玲 石育雄 安永军

摘要：数学建模是对现实问题进行数学抽象，用数学语言发现问题、用数学方法构建模型解决问题的素养。本文以《几何概型的应用》教学为例，从教学设计的角度，精心设计其建模过程，不仅能够让学生掌握数学建模的方法，提高学生解决实际问题的能力，还能够促进学生数学核心素养的养成。

关键词：数学建模;教学设计;几何概型的应用

中图分类号：A 文献标识码：A 文章编号：（2021）-32-457

数学建模是通过对实际教学问题的简化和抽象后，用数学原理建立模型，再解决相关的问题。在高中数学教学设计中，教师想要渗透数学建模素养，应将其融入在教学目标、教学重难点、教学过程、教学总结等各个环节，从而使学生能够针对数学问题开展猜想与交流，实施探究活动，建立数学模型，解决实际问题。几何概型作为新课标新增加的知识点，与生活实际紧密相关，同时与几何论证、计算等方面也有关联，因此在高考中出现的可能性较大，作为教师应该有效设计教案，帮助学生掌握相关知识与技能。

一、问题引求知

教学目标是一切活动设计的中心点与落脚点。因此教师应在教学目标中体现出建模素养，如将实际问题转变为数学问题，使学生通过猜想、探究掌握几何概型的应用能力等。几何概型主要是用来计算基本事件可“连续”发生的有关概率问题，大多数是实际生产、生活问题。因此教师在教学设计过程中，可以采用生活類的问题，激发学生的求知欲望。既能够满足教学目标要求，也能够激发学生的探索欲望。例如，公交车是高中生经常接触的交通工具，为此教师便可以为学生创设一个生活问题情境，公交车站每隔15分钟便会有一辆公交车到达，但是我们到公交车站的时间是任意的，求你到达车站候车时间大于10分钟的概率。

二、猜想引交流

当问题提出之后，教师一定要给予学生时间进行有效的猜想与交流，从而使学生打开探究思路，更好地解决数学问题。因此数学教师需要在教学设计中预留时间空间，让学生发挥主动性。为了将建模素养更好地落实，此时教师便需要引导学生在猜想与交流中，将实际的生活问题转变为具体的数学问题。

首先，该问题是与长度有关的几何概型问题，那么学生在猜想时，首先要找到几何区域D，紧接着找到事件发生在区域D对应的区间d，在此过程中，学生需要找到一个关键点，即确定边界点，但是边界点是否取到并不会对事件的概率产生影响。

三、探究引思考

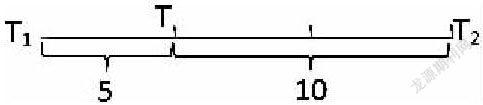
学生对该题进行分析，将时刻抽象为点，时间为线段，利用几何概型的相关知识进行解答。首先设前一辆公交车达到的时刻是T1，下一辆公交车到达的时刻是T2，此时根据题意，我们可以知道T1T2的长度为15，假设T是线段T1T2下标上的某个点，T1T的长度是5，TT2的长度是10（如图）。

当图形绘制之后，教师再让学生进行自主思考与探究，也可以与同桌进行相互交流，以此保证学生的“用脑”频率，使学生始终处于思考状态。思考过后，教师可以让学生进行自主分享，提出自己的探索经过。

学生1说：“当我去坐车的时候，将等车时间大于10分钟当作事件1，如果我到达车站的时刻t落在线段T1T之间，事件1发生。因为区域D的总长度是15，那么我等待事件超过10分钟的区间d的长度是5，即：P1=d的长度D的长度=515=13，所以可以得出我等车时间超过10分钟的概率是三分之一。

四、训练引巩固

为了切实加强学生的建模素养，教师可以在该题的基础上进行延伸与演变，使学生进一步探索更多的数学奥秘，并巩固目前学到的知识。如公交车每隔15分钟到达一辆，每辆车会在站牌处停留3分钟，此时再求等车时间大于10分钟的概率。

该题在前一题的基础上增加了难度，学生需要在之前的数学模型上进行调整才能解决该问题。此时教师可以给学生一点提示，如教师为学生绘制一个图形。

当图形绘制完毕之后，很多学生便有思路，继续按照该模型进行求解，此时设等车时间大于10分钟的事件为A，此时我们到站时刻t便会落在T1T，所以就是P1=T1TT2T2=215

五、总结引完善

在课堂的结尾处，为了验证模型是否符合实际生活中的问题，教师可以带领学生进行结果验证，此时也可以向学生列举更多相关的生活问题进行解释，使学生进一步理解几何概型的模型。最后，教师让学生总结出几何概型的数学模型，即先确定区域D，再确定事件落在区域D中相对应的区间d，最后求出概率。

高中数学建模思想的培养和数学建模的应用是数学教育的重要内容，教师在教学中应重视学生的建模思想和建模素养的培养，加强学生建模意识，提高学生课堂建模方法的能力，并鼓励学生通过观察、思考和论证等方法建立模型。同时，数学学习作为一个与生活息息相关的话题，离不开既定的生活环境，教师的目标是提高学生解决实际问题的能力，使学生善于观察和总结数学生活的规律，强化建模思维在生活中的应用，促进学生数学综合素养的全面提升。

参考文献

[1]张应.在实际问题情境中体验数学建模——问题情境驱动下的高中数学建模教学探讨[J].数学学习与研究，2021（19）：14-15.

[2]陈龙珠.高中数学建模的教学探究——以概率与统计教学内容为例[J].福建教育学院学报，2021，22（06）：22-24.