学科育人视角下数学探究型课堂设计的思考

梁舒尹

[摘   要]统计是数学的重要组成部分，常与生活中的问题密切相关，因此学生要具备基本的数据分析能力。教学设计以制定水费标准实例为背景，通过设置问题串，层层递进，引导学生探究性地学习频率分布直方图，学会利用样本分布估计总体分布，理解其作为重要统计图表的合理性与必要性，体会统计思想，实现思维育人、学科育人。

[关键词]问题导学;频率分布直方图;探究型课堂;数学建模

[中图分类号]   G633.6        [文献标识码]   A        [文章编号]   1674-6058（2021）24-0043-03

数学探究课，就是在教师引导下学生参与包括探索、发现在内的获得知识全过程的课型。探究课中如何体现学科教学的育人功能，需要教师的精心设计。本文以《用样本的频率分布估计总体分布》教学设计为例，谈谈笔者的思考。

本课内容是在学生系统学习基本抽样方法之后，掌握如何整理、分析数据，从而利用样本分布估计总体分布。即将学习的用样本的数字特征估计总体的数字特征以本课内容为基础，故本课具有承上启下的关键作用。本节课笔者以生活实例为背景，引导学生从发现问题——水资源缺乏，到提出问题——如何制定合理的用水标准，倡导节约用水，再到解决问题——利用频率分布直方图，合理地制定标准，运用统计相关知识解决问题。笔者着重从培养兴趣、指导方法、鼓励质疑、鼓励创新四个方面，挖掘学科育人的内容，培养学生的数学素养，强化思维育人，落实立德树人目标。以下是五个具体的教学环节。

一、新课引入

【引例】某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，即确定一个居民月用水量标准[a]，用水量不超过[a]的部分按平价收费，超出[a]的部分按议价收费。如果希望大部分居民的日常生活不受影响，那么标准[a]定为多少比较合理呢？

【问题1】你认为，为了较合理地定出这个标准，需要做哪些工作？

【设计意图】通过播放热点事件——印度水危机的相关视频引入课堂，引导学生感受水资源的珍贵，增加其作为地球人的责任感，让学生关注视频中出现的各种统计图表。统计图表的直观性是单纯的大量具体数据不具备的，故其在大数据时代传递信息中心扮演着重要角色。统计问题常常与生活息息相关，所以学生对频率分布表及频率分布图的学习是必要的。接着，笔者自然地抛出课本的引例，并提出问题1。这样的设计能迅速抓住学生的注意力，激發其求知欲，培养其数学建模核心素养，让其感受到学习本课内容的重要性、实用性及趣味性。

二、概念形成

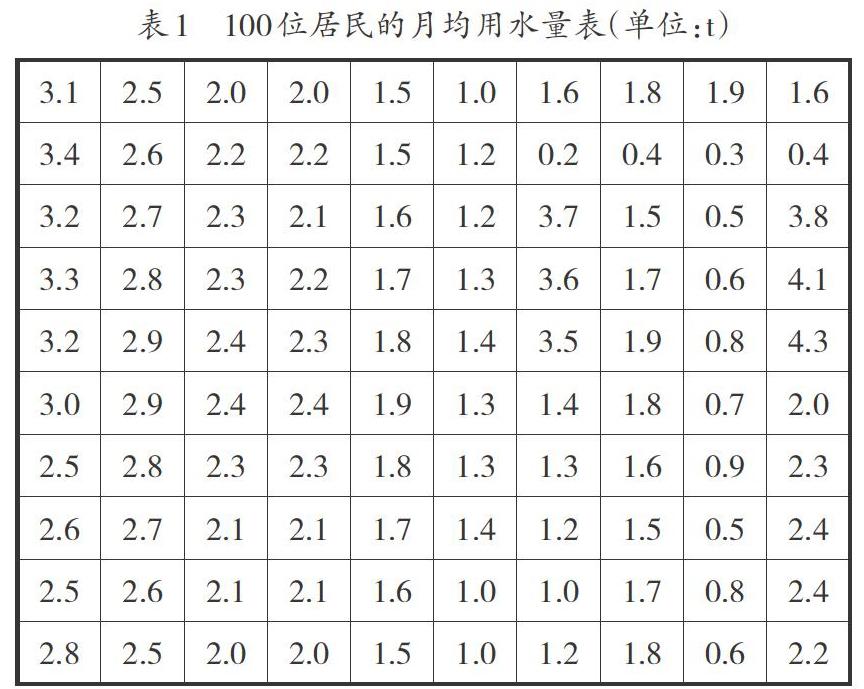
【问题2】如何根据表1的样本数据了解居民用水分布情况？

【设计意图】组织学生对问题2进行讨论，以小组讨论的形式，让学生发散思维，主动分享自己的观点，激发其学习的主动性。培养学生看问题时注重本质、去粗存精、去伪存真、触类旁通，提高抽象概括的能力。同时，让学生了解推理的基本程序，按规则办事。注重学科育人就是注重理性精神的培育，引领学生追求真理、实事求是、不断创新，这是数学教师义不容辞的责任。学生从已有的知识储备，容易想到频数分布直方图。

【问题3】如何根据数据，画频数分布直方图？画频数分布直方图的步骤。

1.计算最大值和最小值的差。

2.决定组距和组数。

3.列频数分布表。

4.画频数分布直方图。

追问：如何分组？应该考虑哪些因素？

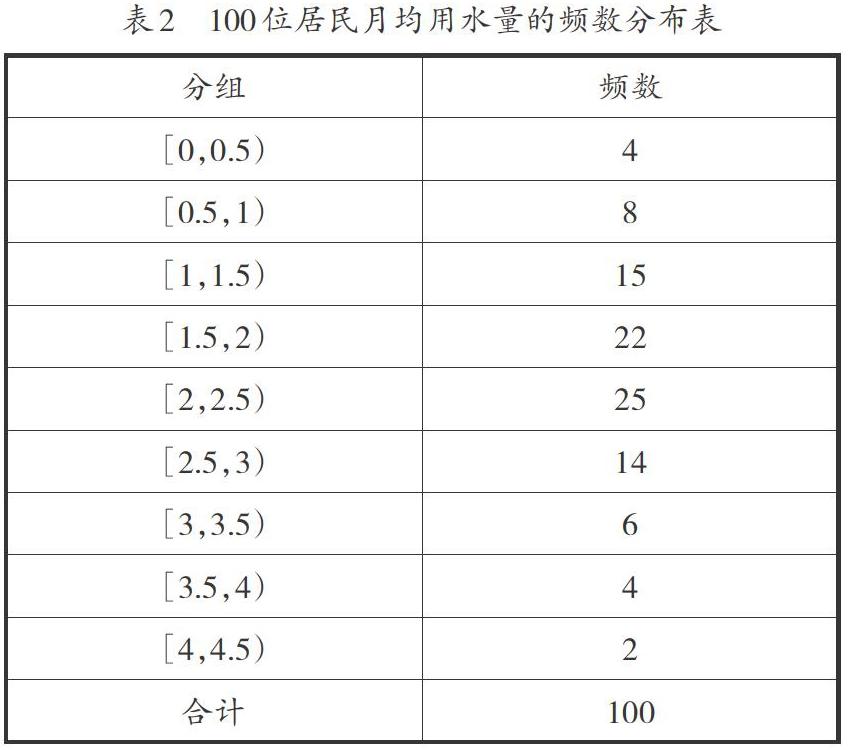
【设计意图】根据问题3复习频数分布直方图，为后面类比学习频率分布直方图奠定基础。特别针对第2步分组进行追问，引导学生注意在分组时考虑数据的范围和个数，组数太多或太少都不能较好地呈现数据的分布规律，组距的选择力求“取整”，组数=[极差组距]。根据统计学经验，当样本容量不超过100时，按照数据的多少，常分为5到12组，如表2所示。在分组的过程中体会统计思维与确定性思维的差异，突破第一个教学难点。

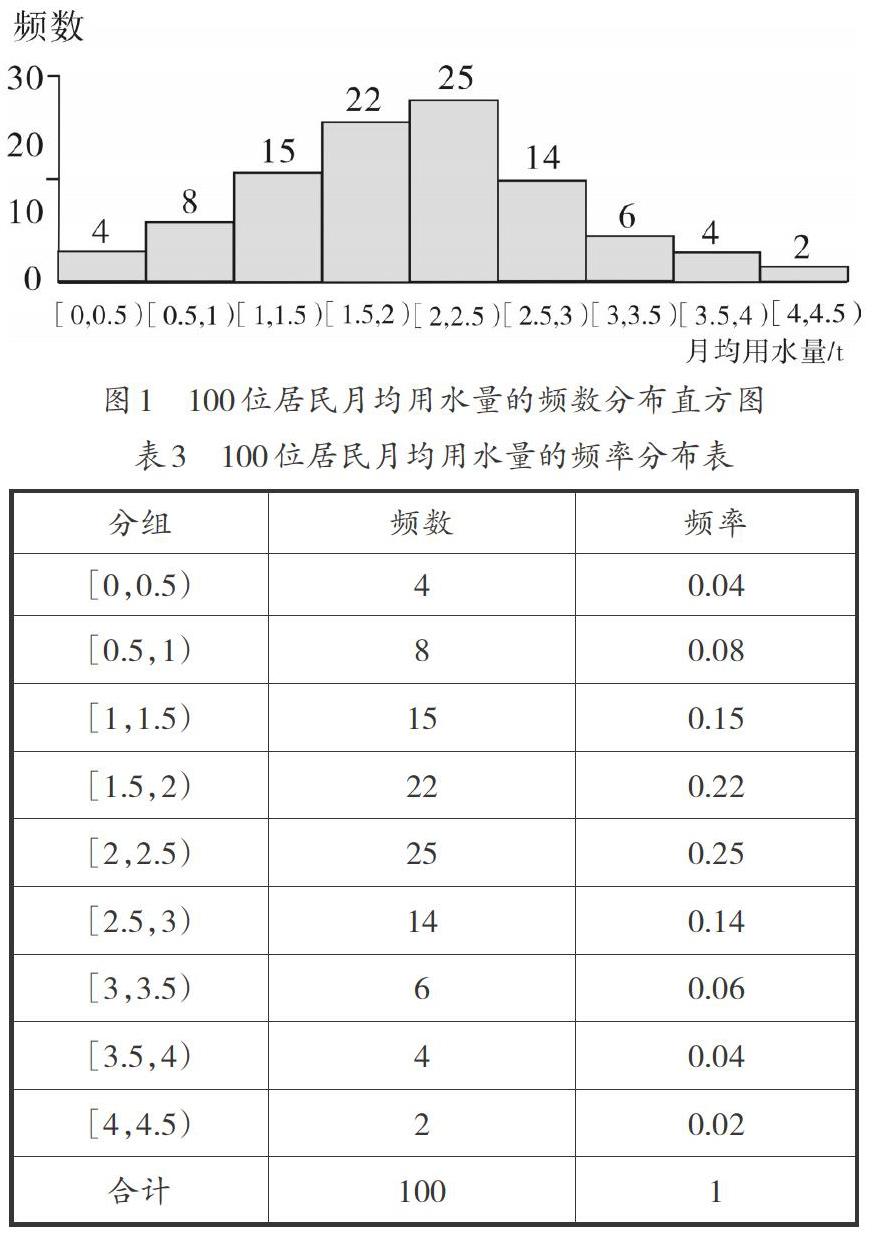
【问题4】根据图1，你能估计50%居民的用水量不超过多少吗？

【问题5】用小矩形的高度表示频率不够直观，用什么“几何量”表示频率更直观？

【设计意图】通过对问题4的思考，学生发现要估计50%居民的用水量不超过多少需要转化为人数的多少再去寻找对应的用水量，因此频数分布直方图虽然可以估计总体分布，但不够直观，违背统计图本身的意义所在。因此，进一步引导学生思考如何改进会让该图更直观？学生自然会想到要用纵轴直接表示频率。结合改进后的统计图，引导学生继续观察，发现用小矩形的高度表示频率，相比频数分布直方图确实直观些，但是从图中我们仍不能直观看出各组频率累积后的大小情况，因此会进一步思考问题5。学生联想之前所学的知识，发现在饼图中，面积表示占比大小，而面积的累积显然比高度的累积更直观，从而凸显频率分布直方图的优越性。笔者不停地激发学生思考，使其不断地发现问题、解决问题，感受到数学是一门精益求精的学科，也能培养其追求卓越的品质。

【问题6】如果小矩形面积表示频率，纵坐标应表示什么？

【设计意图】有了之前累积的学习经验，要使每组矩形的面积表示频率，用纵轴表示[频率组距]。至此，学生对于频率分布直方图有了初步的认识。纵轴从表示频数到频率，再到[频率组距]，根据图1、图2、图3三个统计图的对比，学生基本可以理解在频率分布直方图中纵轴表示[频率组距]的合理性，这突破了教学中的第二个难点。在此过程中培养学生的探究精神、逻辑推理核心素养，渗透数形结合的思想。

三、概念深化

【问题7】整个频率分布直方图中小矩形的面积和是多少？

【设计意图】明确频率分布直方图中矩形的面积和为1，落实知识点。

【问题8】根据频率分布直方图，你能获取哪些信息？

【设计意图】组织学生对问题8进行讨论，引导学生“读”图，联系实际，结合频率分布直方图，运用数学统计语言直观展示居民用水量分布情况。图形的角度呈“山峰”状，且是“单峰”的，还具有一定的对称性，说明大部分居民的月均用水量集中在一个中间值附近，只有少数居民月均用水量很多或很少。学生可进一步体会频率分布直方图通过样本分布估计总体分布也存在局限性，因为原始数据不能在图中体现。这落实了本课的教学重点，培养了学生的分析能力。

【问题9】如果市政府希望[85%]左右的居民月均用水量不超过标准，根据上述频数分布直方图，你对制定居民月均用水量标准（即[a]的取值），有什么建议？

追问：你认为这个标准一定能保证85%以上的居民用水不超标吗？如果不一定，那么哪些环节会导致结论的差别？

【设计意图】回归引例中的问题，提出问题9，引导学生对“面积”进行累积，自主发现有88%的居民用水量不超过3t，那[a]的取值能否定位为3t？3t满足政府的要求。结合实际，将标准定位为3t是个整数，便于水费的缴纳。因此，将标准定位为3t是合理的，可以考虑。为了培养学生形成对数据处理过程进行初步评估的意识，提出追问的问题，引导学生正确理解统计推断的结论，频率分布表和频率分布直方图存在随机性，因此得到的统计结论只是对总体的估计值。

四、应用探索

【问题10】类比画频数分布直方图的步驟，画频率分布直方图的步骤有哪些？

1.计算最大值和最小值的差（即极差）。

2.决定组距和组数。

3.列频率分布表。

4.画频率分布直方图（纵轴表示[频率组距] ）。

【设计意图】类比频数分布直方图，归纳总结频率分布直方图的作图步骤，为后续组织学生动手实操打下基础。

【实验】如果以0.2和1 为组距重新作图，频率分布直方图有什么变化？

【设计意图】通过实验，一方面，让学生自己动手操作画频率分布直方表和频率分布直方图，掌握此技能。另一方面，让学生发现当分组不一样时，同样的数据得到的频率分布直方图结构会发生变化。因此，依照样本数据去推断总体情况会存在偏差，下统计结论是需要进行评估的。

五、总结提高

对本节课内容进行简单的小结。

1.思想：总体抽样得到样本数据，依据样本估计总体。

2.知识与技能：绘制频率分布直方图、频率分布表，会利用样本分布估计总体分布。

3.课后思考1：如果改变样本数据，不改变原有组距，频率分布直方图有什么变化？

课后思考2：如果增加样本数据，不改变原有组距，频率分布直方图有什么变化？

通过课后思考题，引导学生探究频率分布直方图的规律性和随机性，进一步深入理解频率分布直方图。统计知识的学习较为琐碎繁杂，但应用广泛，与我们的生活息息相关。相对于枯燥的概念及公式的讲授，如何在教学过程中让学生感受到统计知识的趣味性与应用性？正如古人所云，“授人以鱼，不如授之以渔”。以问题为依托，环环相扣的探究型课堂教学模式，教师注重引导学生发掘知识的内涵与外延，尊重学生的主体地位，加大学生思维的广度与深度，能够在日常教学中较好地实现思维育人、学科育人！

（责任编辑   黄诺依）