关于“等差数列的前n项和”教学素材、设计案例的思考与研究

祝玲

摘 要：“等差数列的前n项和”的教学设计是一线老师比较喜欢研究的重点课题之一，也是目前赛课较热门的内容之一.再加上目前较多的版本教材，所以有各种各样素材和教学设计案例产生.研究各色素材，发现它们有继承性和创新性，揣摩教学设计和案例，也精彩纷呈，但如何引导学生自然想到公式的推导智者见智，仁者见仁，本末笔者给出可供临时应变的多种途经教学设计.

关键词：等差数列;教学素材;教学设计;案例

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）04-0020-04

一、问题提出

“等差数列的前n项和”的教学设计是一线老师比较喜欢研究的重点课题之一，也是目前赛课较热门的内容之一.因为这节课中公式推导是最令人心驰神往的，也是各类期刊谈论最多的，就是如何引入倒序相加法，推导出等差数列的前n项和公式，可谓仁者见仁，智者见智.笔者一直都在想，目前我们各省市有各种版本教材，对公式的推导设计有何异同？若没有教材上提示或学生事先不预习，推导方法学生会想到吗？学生想不到，老师又如何精心设计教学，引导学生自然而然探究出公式呢？基于以上思考，笔者查阅教科书和有代表性的期刊，进行研究，写下拙文.

二、文献研究

1.各种版本教材对等差数列前n項和公式推导的编写比较

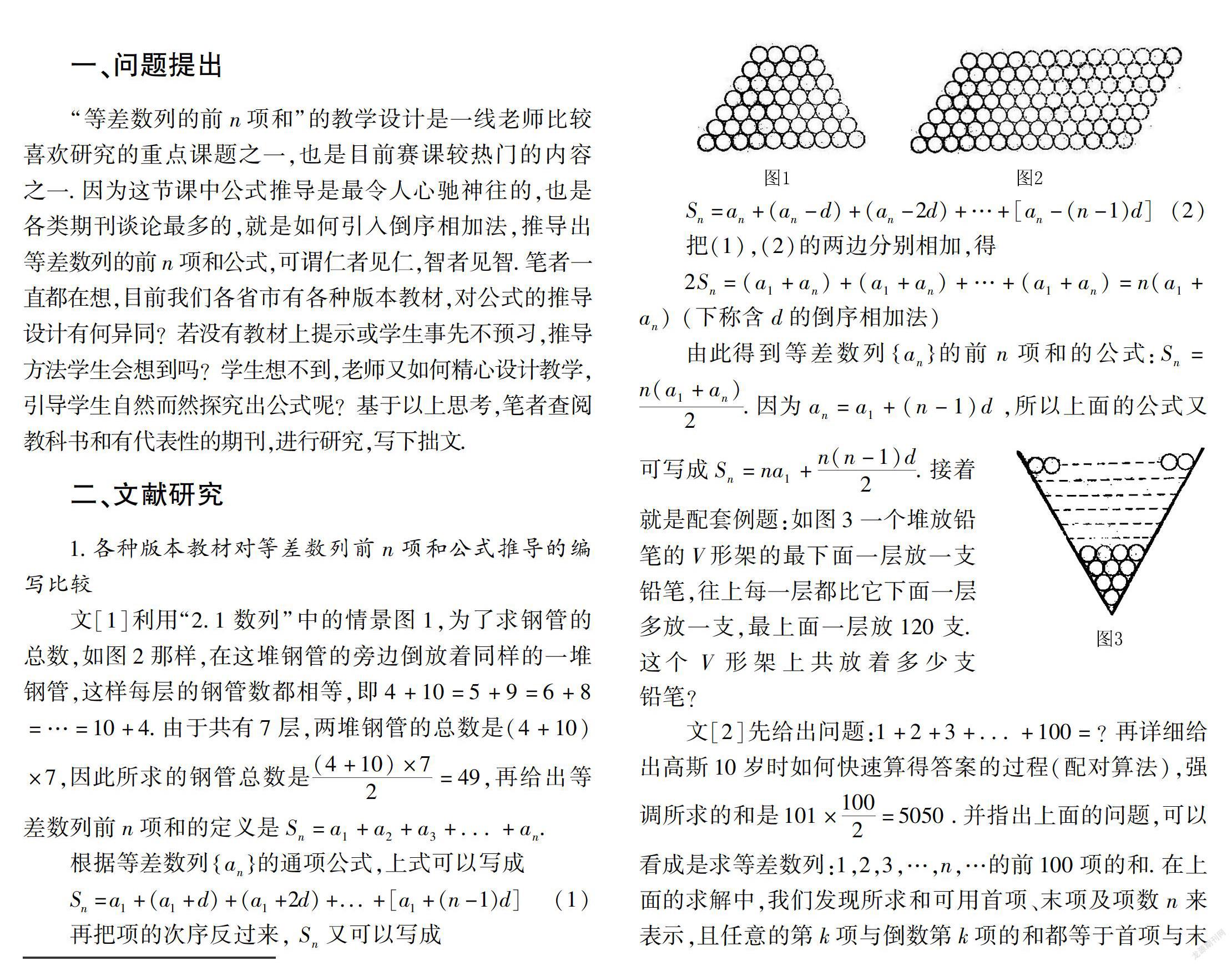
文[1]利用“2.1数列”中的情景图1，为了求钢管的总数，如图2那样，在这堆钢管的旁边倒放着同样的一堆钢管，这样每层的钢管数都相等，即4+10=5+9=6+8=…=10+4.由于共有7层，两堆钢管的总数是（4+10）×7，因此所求的钢管总数是（4+10）×72=49，再给出等差数列前n项和的定义是Sn=a1+a2+a3+...+an.

根据等差数列an的通项公式，上式可以写成

Sn=a1+（a1+d）+（a1+2d）+...+[a1+（n-1）d] （1）

再把项的次序反过来， Sn又可以写成

Sn=an+（an-d）+（an-2d）+…+[an-（n-1）d]（2）

把（1），（2）的两边分别相加，得

2Sn=（a1+an）+（a1+an）+…+（a1+an）=n（a1+an） （下称含d的倒序相加法）

由此得到等差数列an的前n项和的公式：Sn=n（a1+an）2.因为an=a1+（n-1）d ，所以上面的公式又可写成Sn=na1+n（n-1）d2.接着就是配套例题：如图3一个堆放铅笔的V形架的最下面一层放一支铅笔，往上每一层都比它下面一层多放一支，最上面一层放120支.这个V形架上共放着多少支铅笔？

文[2]先给出问题：1+2+3+...+100=？ 再详细给出高斯10岁时如何快速算得答案的过程（配对算法），强调所求的和是101×1002=5050 .并指出上面的问题，可以看成是求等差数列：1，2，3，…，n，…的前100项的和.在上面的求解中，我们发现所求和可用首项、末项及项数n来表示，且任意的第k项与倒数第k项的和都等于首项与末项的和，这就启发我们如何去求一般等差数列的前n项的和，下面和文[1]相同.

文[3]给出高斯的算术老师提出的问题：1+2+3+…+100=？指出高斯采用下列方法迅速算出正确答案：（1+100）+（2+99）+…+（50+51）=101×50=5050.也即说明了高斯解决了等差数列：1，2，3，…，n，…前100项的和的问题.人们从这个算法中受到启发，用下面的方法计算1，2，3，…，n ，…前n项和：由

可知1+2+3+...+n=（n+1）×n2.

再给出探究：高斯的算法妙在哪里？这种方法能够推广到求一般等差数列的前n项和吗？自然给出数列前n项和定义，特别强调由高斯算法的启示，用两种方式表示前n项和Sn，一种是顺序的，一种是倒序的，再相加，类似文[1].

文[4]创设情景：某钢材库新到200根相同的圆木料，要把它们堆放成正三角形垛（如图4），并使剩余的圆木料尽可能的少，那么将剩余多少根圆木料？

设共摆放了n层，能够成三角形垛的圆木料数为Sn，则Sn=1+2+3+…+n.指出这是一个等差数列的求和，如何计算呢？引出高斯小时候求当n=100的算法：有趣的是和文[2]、文[3]“配对求和”不同，这里给出倒序相加的思想方法：

S100=1+2+3+4+...+98+99+100=100+99+98+97+...+3+2+1

这两个等式上、下对应项的和均为101，所以

2S100=101+101+101+...+101+101+101=101×100=10100，最后有Sn=101002=5050

用“你能从这个问题的解决过程中悟出求一般等差数列前n项和的方法吗？”过渡到抽象概括阶段，下同文[1]，但在旁白留有两个问题，用来提炼数学思想方法.推导出公式后，给出它的几何意义如图5，在旁注中再次提及：这种思想方法，用图形来说明就更清楚，在图上拼一个倒过来的图形，就成为各行有相同个数的平行四边形，计算这个平行四边形的个数就很容易了，如图6.

文[5]和文[1]从情景图引入到推出求和公式都一样，只是将钢管由原来7层改为6层，图设计得更精美，如图7.另外笔者也发现，文[5]将文[4]中的情景题放置在第2课时的练习题4中.

文[1]和文[5]由情景设置很容易和“倒序相加法”挂钩，不拖泥带水，单刀直入，学生看一眼就明白，无法进行探究性学习.尽管文[1]、[2]、[3]是人民教育出版社编写的，在后两文中没有继承前者的情景创设，笔者估计由于时代发展，当今小学生和初中生都能知道高斯速算的故事，所以由高斯速算创设情景是可行的.但是“高斯的算法与一般等差数列求和还有一定距离，因此教科书接下来设置了求1+2+3+……+n的问题，目的是引出求等差数列前n项和的一般方法：‘倒序相加法’.这样，很自然地就过渡到一般等差数列求和问题”.

另外，我们无法考证将近250年前高斯到底用何算法，所以文[4]在不损“数学王子”形象情况下，揣测他用“倒序相加法”，实属高明，这样就为下面推导作好做好铺垫，而不使人误入歧途.另外五个版本教材都没有利用等差数列性质，采用如下写法：

Sn=a1+a2+a3+...+an-2+an-1+an（1）

Sn=an+an-1+an-2+...+a3+a2+a1（2）

两式相加得2Sn=（a1+an）+（a2+an-1）+...+（an+a1）=n（a1+an），即Sn=n（a1+an）2

（下称不含d的倒序相加法）.

2.各种期刊对等差数列前n项和公式推导教学设计案例的比较

由于教材不同，加上每个老师对教材理解不同，学生学习程度不同，产生许多精彩纷呈的教学设计.

文[7]创设生活中的一个问题，引入新课：学校为美化校园，决定在道路旁摆放盆景.从校门口取出花盆到距校门1m处开始摆放，每隔1m摆放一盆，学生小王每次拿2盆，若要完成摆放30盆的任务，最后返回校门处，问小王走过的总路程是多少？

问题转化求4+8+12 +…+60 =？出示课题，给出前n项和Sn的定义，重新叫学生计算：1+2+3+4 +…+100 =？（高斯10岁时的算法）.

老师又给出变式：1+2+3+…+99 =？

方法1 原式=（1+2+3+4+…+98+99+100） - 100.

方法2 原式=（1+2+3+4+…+98）+99.

方法3 原式= 0+1+2+3 +…+98+99

方法4 原式= （1+2+3 +…+49+51 +…+98+99）+50

方法5 原式= （1+2+3 +…+97+98+99+99+98+97 +…+3+2 +1）÷2

T：那么，1+2+3 +…+n=？紧接着教师追问和“启发”，好似硬拉学生用“倒序相加法”推导出：Sn=n（n+1）2，仿照此法，用不含d的倒序相加法推导出等差数列an的前n项和公式，老师从另一个角度再次推导：Sn=a1+（a1+d）+…+[a1+（n-1）d]=na1+[1+2+…+（n-1）]d=na1+n（n-1）d2 ，这样将“1+2+3 +…+n=？”作用发挥出来了.例题中用《张丘建算经》中的“女子织布”问题用以变换问题情境，灵活运用公式.

思考 给出的情景题贴近学生的生活，只是又要用高斯速算问题，多花时间，又显得不紧凑.老师给出的变式非常好，产生后续五种方法，其中法五就是“倒序相加法”的雏形，再计算1+2+3 +…+n=？，自然就会方法纷呈，讨论奇偶性再配对或倒序相加法，无论怎样都能推导出公式，如果学生硬要走Sn=a1+（a1+d）+…+[a1+（n-1）d]=na1+[1+2+…+（n-1）]d=na1+n（n-1）d2这条路，老师将学生引导到“倒序相加法”就需要智慧了，可惜文中没有体现.

文[8]首先設计问题，创设情境.教师给出高斯小时候算过的问题1：求 1+2+3 +…+100=？学生中出现“配对求和”和“倒序相加法”.

问题2：如图8，是一垛钢管，最下面一层放了102 根，最上面一层放了3根，往上每一层都比它下面一层少放一根.这垛钢管共放了多少根钢管？

不一会儿，就有学生举手回答：由等差数列的通项公式易知，这垛钢管共100层，由图8联想到梯形的面积公式的推导方法，用类似的方法去想.如图9所示，可以看出图2每层均有3+102根，又知共 100层，故共有（3+102）×100 根.从而得到（图8中）钢管的根数为：（3+102）×1002=5250.接着教师抛出开放性问题：由问题1及问题2，同学们能想到些什么问题吗？学生提出求 1+2+3 +…+n=？并对结果和计算方法进行探讨，得到求解此题的“倒序相加法”，根据问题1和2的结果，最后有学生猜想出等差数列an的前n项和的计算公式：Sn=n（a1+an）2.老师再叫学生探索，证明猜想，用归纳推理的有之，利用“1+2+3 +…+n =”结果的有之，用倒序相加法的有之.

思考 文中的两个问题，起了“双保险”的作用，若学生由问题1想不到倒序相加法，则问题2可以帮助学生想到;若第1问就能想到倒序相加法，则第二问题就是对倒序相加法的几何解释.“配对求和”是深入人心的方法.

文[9]问题1：用文[1]例题，只是将“120”改为“100”，进而引出求数列：1，2，3，4…100，…的前100项和，从而给出数列an前n项和的定义，点明主旨.师生共同探讨S100=1+2+3 +…+100=？师生达成一致，用“配对分组”手段解决问题1.随后给出点睛之笔：高斯算法的高明之处在于将不同数的求和问题转化为相同数的求和问题.

问题2：求Sn=1+2+3 +…+n=？（n∈N*）学生自主探究，给出配对求和（对n分奇偶讨论）和倒序相加法;最后再研究问题3：求等差数列an前n项和：

Sn=a1+a2+a3+…+an，学生想到不含d的倒序相加法求和得Sn=n（a1+an）2，和用“1+2+3 +…+n=？”结论求和得Sn=na1+n（n-1）d2.

通过例1求梯形笔架中笔的支数，对倒序相加法作出几何解释，如下图11-13.

思考 求V形架里铅笔支数这一生活问题既经济又实惠，取材学生身边问题，又能顾及到高斯的算法，还能为学生推导第二个求和公式服务，一箭三雕.难能可贵的是指明求和的本质就是“将不同数的求和问题转化为相同数的求和问题”，这是本节课精髓所在，也是对倒序相加法最合理的解释.在例题中没有进行操练，而是通过问题再深入理解公式，领会这两个公式的内在联系.

三、尝试设计

图1

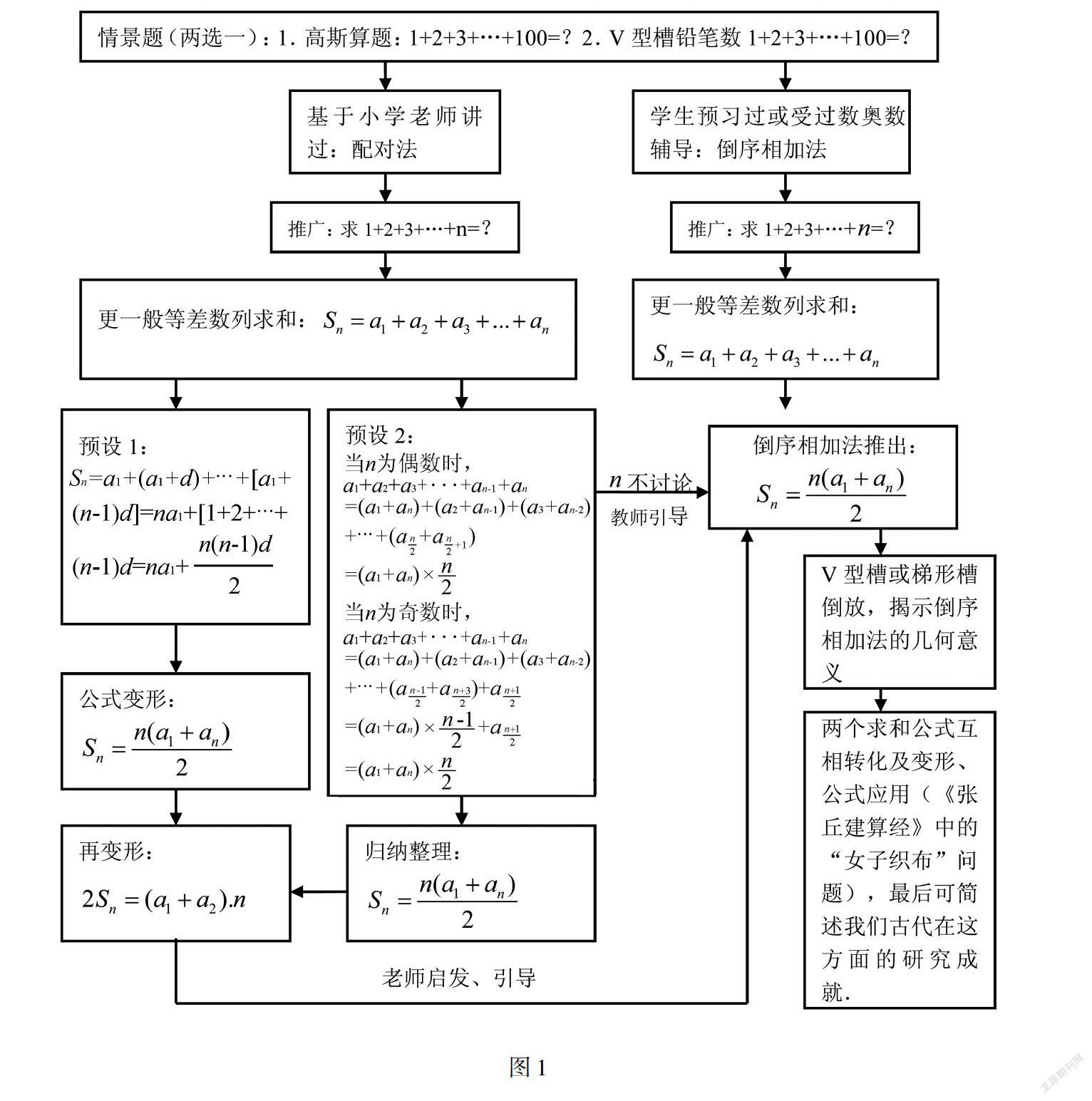
“操千曲而后晓声，观千剑而后识器”，笔者在学习了诸多优秀教学设计后，博采众长，从顺应学生思维自然性，符合学生认知规律出发，给出如下教学设计思路的框图1所示.

教材呈现知识点限于编排要求具有经典性、纲要性、简洁性，不可能像教辅用书上洋洋洒洒详细阐述，关键是教师在备课时要了解学生受教育的背景，近期上课内容对该堂课的引领作用.此外不光有自己的想法，还要想学生所想，顺着学生思维流程进行教学，这样既不动声色传授了核心知识，又潜移默化培养学生的研究能力.

参考文献：

[1]人民教育出版社数学室.高级中学课本（甲种本）代数第二册[M].北京：人民教育出版社，1984：47-49.

[2]人民教育出版社中学数学室.全日制普通高级中学教科书（必修）数学第一册（上）[M].北京：人民教育出版社，2003：115-116.

[3]刘绍学.普通高中数学课程标准实验教科书《数学必修5》[M].北京：人民教育出版社，2007：42-43.

[4]严士健，王尚志.普通高中数学课程标准实验教科书《数学必修5》[M].北京：北京师范大学出版社，2007：17-18.

[5]单墫.普通高中数学课程标准实验教科书《数学必修5》[M].江苏：江苏教育出版社，2008：40-41.

[6]刘绍学.普通高中数学课程标准实验教科书《数学5教师教学用书》[M].北京：人民教育出版社，2007：44.

[7]朱利强，李芳等.等差数列的前n项和（第一课时）[J].中学数学，2004（3）：16-17.

[8]王文清，阮红霞.“自主学习与创新意识培养数学课堂教学模式”研究课一例——“等差数列前n项和”教学实录[J].中学数学杂志（高中），2005（1）：14-15.

[9]钱卫红.等差数列的前n项和（第一课时）教学实录[J].中小学数学（高中版），2009（7-8）：15-17.

[责任编辑：李 璟]