“图形的轴对称、平移和旋转”中考专题复习教学设计
曹自由 初雨
摘 要:图形的变化是发展空间观念的内容抓手,也是研究图形的基本方法,是发现和构造不变量和不变关系的重要途径. 学生在新授课阶段分别学习了轴对称、平移和旋转,在中考第二轮复习中需要建立它们之间的关联,进行整体复习. 通过四个课时的复习教学,分别引导学生感受运动变化、理解运动变化、运用运动变化、整合运动变化,有效发展学生的空间观念、几何直观和推理能力. 文章将第1课时设计整理成文,以供研讨.
关键词:图形的变化;中考复习;教学设计
一、内容和内容解析
1. 内容
图形的变化(轴对称、平移、旋转).
2. 内容解析
初中阶段学习的几何图形的变化包括轴对称、平移、旋转和相似(位似)的概念、性质和应用. 本节课复习的内容是图形的全等变换——轴对称、平移和旋转.
图形的全等变换可以看作是图形的刚体运动,用全等变换的思想研究图形的性质和关系是“图形与几何”领域重要的学习内容. 在义务教育阶段,图形之间最重要的关系就是全等,全等可以用图形重合的方式直观获得,而“图形重合”需要通过图形的运动来实现,这种运动就是图形的轴对称、平移和旋转. 图形的变化是理解图形空间结构的基本方法,也是空间观念的核心要素. 抽象轴对称、平移和旋转的基本性质,用逻辑的方法理解图形的全等变换是从定性到定量研究图形的变化的桥梁. 从小学直观认识图形的轴对称、平移和旋转到初中的逻辑研究、坐标表示再到后续的矩阵表示,是图形的全等变换的定性到定量发展的三个重要阶段.
基于以上分析,确定本节课的教学重点是:建立三种图形的变化相关知识的逻辑体系,并用图形变化的观点认识几何图形.
二、目标和目标解析
1. 目标
(1)理解轴对称、平移、旋转之间的联系,加深对运动变化的认识,落实画图和识图的能力,渗透几何直观能力.
(2)在问题探究的过程中,逐步形成用图形的变化思考、解决问题的意识,渗透图形变化思想.
2. 目标解析
达成目标(1)的标志:能够从运动变化的角度描述两个已知图形之间的关系,能够根据图形变化(轴对称、平移、旋转)的概念和性质画出运动变化后的图形,通过梳理建立三种变化相关知识的逻辑体系.
达成目标(2)的标志:能够以运动的视角观察图形,用变化的思想分析图形特征.
三、教学问题诊断分析
近几年北京中考试卷中的几何综合题都考查了图形的变化的相关内容,并且不是单一的,而是从一种变化到另一种变化的综合考查. 但是学生学习时,知识是零散的、分割开的,先学习了平移,然后是轴对称和旋转,没有形成三种变化相关知识的逻辑体系. 同时,图形的变化是一种观察图形的视角,培养这种“视角”与培养“知识与技能”同样重要.
基于以上分析,可以确定本节课的教学难点是:三种图形的变化之间的转化.
四、教学过程设计
1. 课前学习
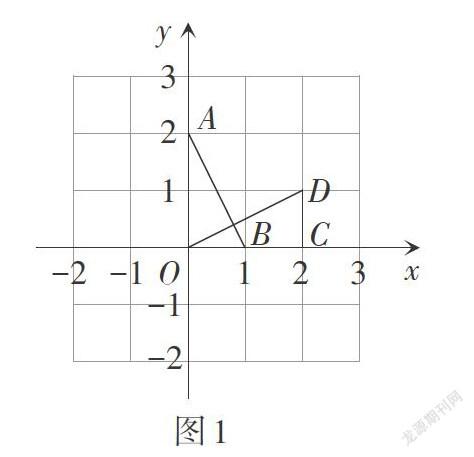
题目 如图1,在平面直角坐标系[xOy]中,[△AOB]可以看作是[△OCD]经过若干次图形的变化(轴对称、平移、旋转)得到的,写出一种由[△OCD]得到[△AOB]的过程: .
思考问题:什么是轴对称、平移、旋转?它们各有什么性质?它们之间有什么联系?
【设计意图】此题为2017年中考北京卷第15题,学生在课前复习轴对称、平移、旋转的相关知识,关注知识的形成过程及知识之间的内在联系,在应用中不断深化认识. 通过解决中考试题回顾思考涉及的知识和思想方法,进一步提升能力.
2. 交流梳理
环节1:交流课前学习成果.
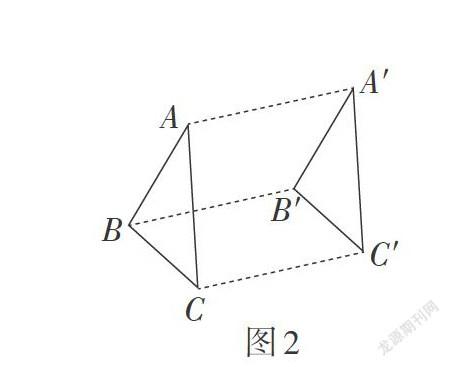
(1)平移:如图2,平移前后的两个图形全等(从图形形状、大小关系来看);对应线段平行且相等,两对应点连线互相平行(共线)且相等(从图形位置变化来看).
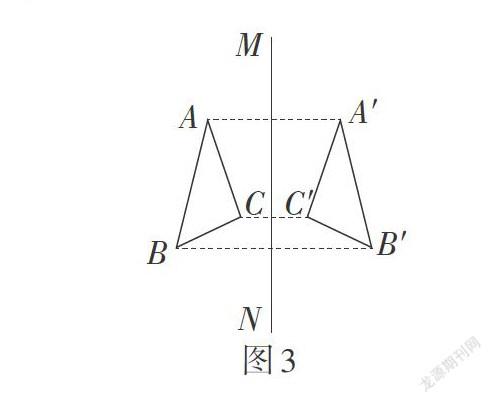
(2)轴对称:如图3,关于某直线对称的两个图形全等(从图形形状、大小关系来看);对应线段相等,两个图形关于某直线对称,那么对称轴是任意一对对应点所连线段的垂直平分线(从图形位置变化来看).
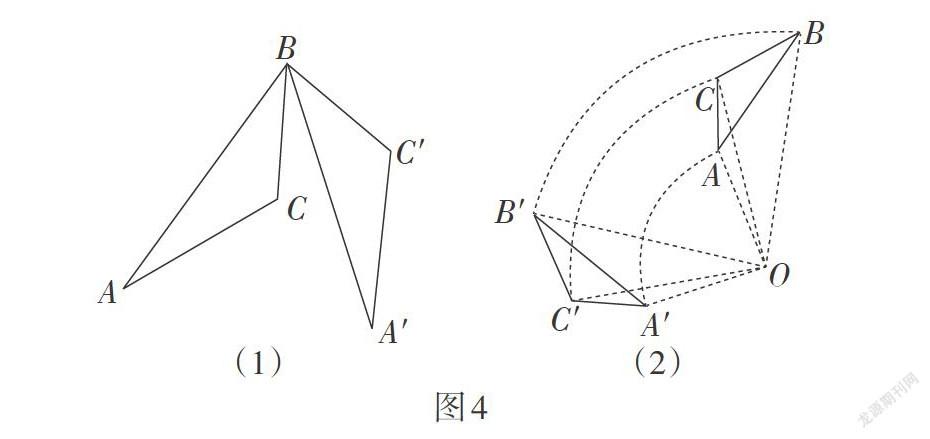
(3)旋转:如图4,旋转前后的两个图形全等(从图形形状、大小关系来看);每两对对应点连线所形成的角都等于旋转角(从图形位置变化来看);对应点到旋转中心的距离相等(从图形位置变化来看).
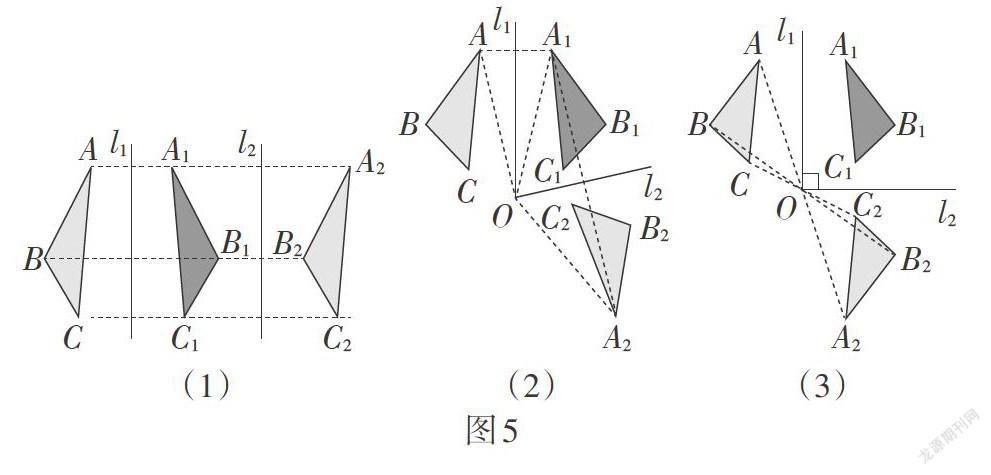
(4)轴对称、平移、旋转三者的关系:如图5,两条对称轴平行的轴对称复合[⇔]一次平移;两条对称轴相交的轴对称复合[⇔]一次旋转.
轴对称在三种变化中起到桥梁作用,轴对称与另外两种全等变换在地位上是有区别的,它是更加基础的一种变化,所有平移、旋转都可以用轴对称变化来解释.
【设计意图】学生先回答思考问题,借此梳理三种变化的性质,明确各自的画图方法及依据,明确三种变化之间的关系.
环节2:问题引导深入思考.
思考:只用一種变化可不可以操作?如何操作?用两种变化如何操作?哪种方法容易快速想到?为什么?
【设计意图】课上让学生先交流自己的结果. 而学生在交流结果时一定是无序的,这时教师可以引导学生进行有序思考.
问题1:对于题目,只用两种变化有哪些方法?
学生活动:交流使用两种变化的情况.
(1)旋转 + 平移.
思路1:将△COD绕点C顺时针旋转90°后,再向左平移两个单位得到△AOB.
思路2:将△COD绕点O顺时针旋转90°后,再向上平移两个单位得到△AOB.
思路3:将△COD向左平移两个单位后,再绕点C顺时针旋转90°得到△AOB.
思路4:将△COD向上平移两个单位后,再绕点A顺时针旋转90°得到△AOB.
(2)旋转 + 轴对称.
思路5:将△COD先关于x轴对称,再以点C为旋转中心顺时针旋转90°,再作关于直线x = 1的对称得到△AOB.
追问:采用“平移 + 轴对称”的方式可以吗?
归纳:对应顶点排列的顺序一致——旋转;与目标图形的方向一致——平移.
问题2:用一种变化有哪些方法?
追问:两个全等的三角形通过某种运动方式一定能重合吗?若能重合,如何运动?
归纳:对应顶点排列顺序一致,经过一次旋转能重合.
学生活动:对于题目,展示只通过旋转或只通过轴对称完成任务的方法,并说明自己的画图方法和画图依据.
方法1:(旋转)根据旋转的性质,确定旋转中心、旋转方向和旋转角.
思路6:将△COD绕点[1,1]顺时针旋转90°得到△AOB.
思路7:将△COD先绕点[1,-1]逆时针旋转90°后,再绕点O旋转180°得到△AOB.
方法2:(轴对称)两条对称轴相交的轴对称复合[⇔]一次旋转.
思路8:先将△COD沿直线x = 1对称后,再沿直线y = x对称得到△AOB.
思路9:先将△COD沿直线y = 1对称后,再沿直线y = -x + 2对称得到△AOB.
【设计意图】题目难度不大,且学生具备直接识别运动变化的能力,但是学生自己描述运动变化的经验还是比较少的,而且运动的方式是不唯一的,给出运动前后的图形,描述运动变化要素,这对学生的要求实际上是提高了很多的. 因此,要关注这三种运动变化之间的联系,通过这个过程深化学生对于运动变化的认识.
3. 变式练习
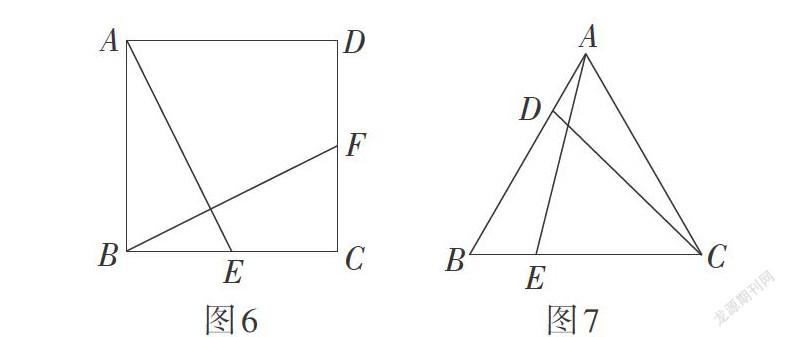
变式1:如图6,在正方形ABCD中,点E,F分别是BC,CD的中点,试类比上一个问题的探究过程,说出△ABE经过怎样的图形的变化(平移、轴对称、旋转)得到△BCF?
变式2:如图7,在等边三角形ABC中,AD = BE,试类比上一个问题的探究过程,说出△ABE经过怎样的图形的变化(轴对称、平移、旋转)得到△CAD?
学生活动:展示所画图形的变化过程,并用语言描述这个过程. 学生可能想到如下情况.
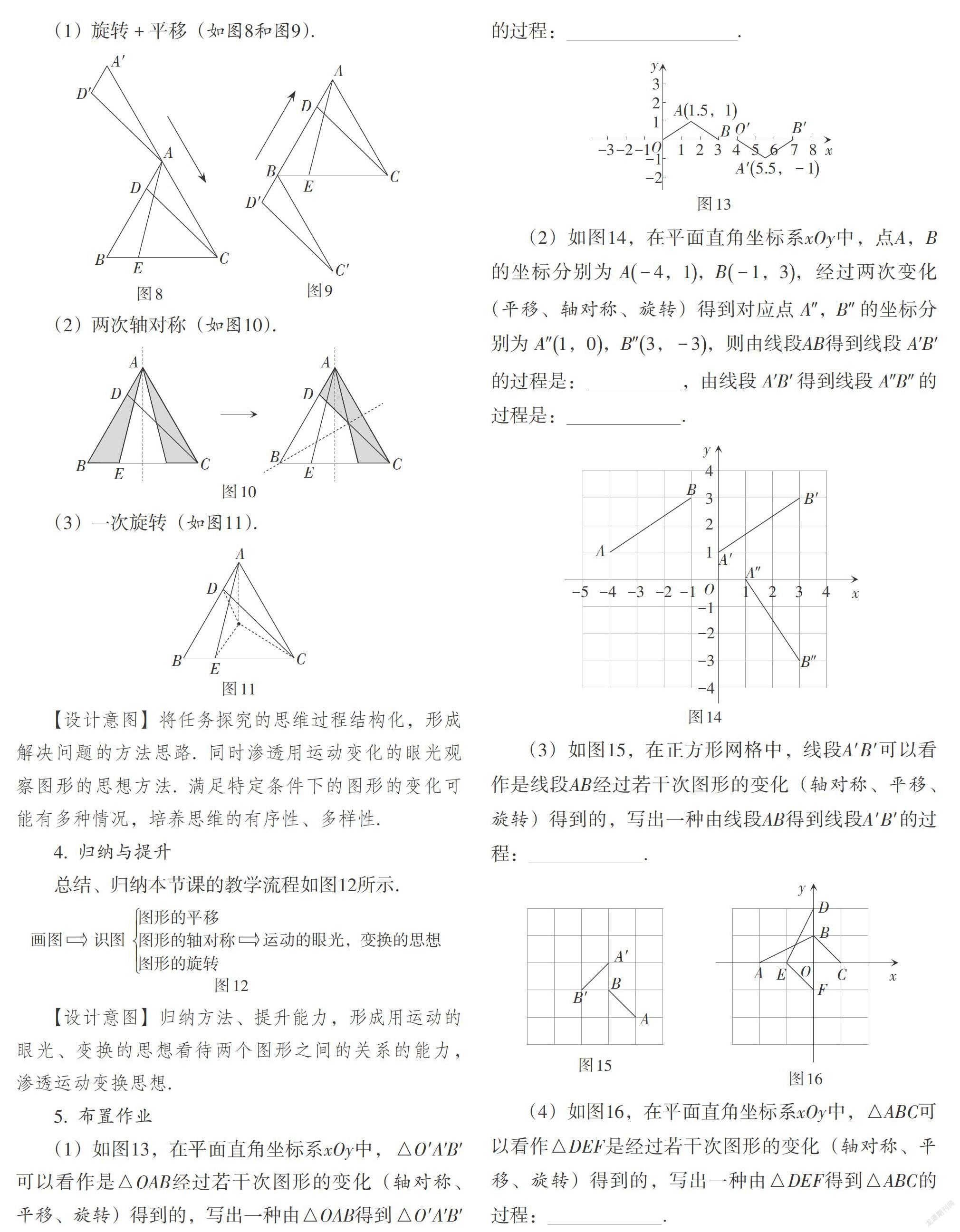
(1)旋转 + 平移(如图8和图9).
(2)两次轴对称(如图10).
(3)一次旋转(如图11).
【设计意图】将任务探究的思维过程结构化,形成解决问题的方法思路. 同时渗透用运动变化的眼光观察图形的思想方法. 满足特定条件下的图形的变化可能有多种情况,培养思维的有序性、多样性.
4. 归纳与提升
总结、归纳本节课的教学流程如图12所示.
【设计意图】归纳方法、提升能力,形成用运动的眼光、变换的思想看待两个图形之间的关系的能力,渗透运动变换思想.
5. 布置作业
五、教学反思
本节课是“图形的轴对称、平移和旋转”中考第二轮专题复习课,内容属于“图形的变化”. 希望通过一系列数学活动,帮助学生在已有知识基础上对图形变换思想进行相应的概括和应用. 同时,在落实“四基”、培养“四能”的过程中,促进学生数学学科核心素养的形成和发展.
1. 感受运动变化,建立逻辑体系
学生通过亲身经历课前的数学操作活动后,体验的水平停留在“感觉”阶段,还没有对活动过程进行深入的思考,没有深刻认识到三种全等变换之间内在的逻辑关系. 在此基础上,学生在课堂上通过交流及反思性观察将获得的体验进行抽象,梳理三种全等变换各自的性质及它们之间的联系,形成解决该类问题的一般思维模式. 图形的变化是一种观察图形的视角,培养这种“视角”与培养“知识与技能”同样重要.
在关注联系的基础上,通过问题引导,使学生能够进行知识的归纳梳理,并能够主动利用经验的迁移去研究其他问题. 通过本节课的教学,进一步帮助学生感受运动变化,学会以运动变化的视角分析图形,也为后续进一步主动运用图形变化视角认识几何图形,运用图形变换思想解决综合性问题奠定基础.
2. 培养思维的有序性、多样性
满足特定条件下的图形的变化可能有多种情况,开放性问题有助于学生体验解决问题方法的多样性. 与此同时,通过增加限定条件,从两种图形变化的组合,到只用一种图形变化,将任务探究的思维过程结构化,形成解决问题的方法思路. 同时,渗透用运动变化的眼光观察图形的思想方法.
本节课的教学目标定位在落实画图和识图能力,渗透几何直观能力,理解轴对称、平移、旋转之间的联系,加深对运动变化的认识;在问题探究的过程中,逐步形成用图形的变化视角思考解决问题的意识,渗透图形变化思想. 在实际授课過程中,知识与技能落实得比较到位,而思想性体现不够充分,还需要深入研究,在思想性上多做文章.
参考文献:
[1]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[2]教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准(2011年版)》解读[M]. 北京:北京师范大学出版社,2012.
[3]章建跃. 章建跃数学教育随想录[M]. 杭州:浙江教育出版社,2017.
[4]任华中,傅海伦,邵亚娜. 初中数学基本活动经验的教学目标层次划分[J]. 中国数学教育(初中版),2018(6):30-32.

