聚焦符号抽象、推理和运算的“方程与不等式”专题复习教学设计与思考
郑燕红



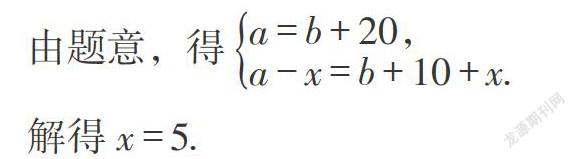

摘 要:方程和不等式是对含有字母符号的两个代数式表示量的大小关系的进一步研究,是初中代数领域中符号抽象、运算和推理基本思想的具体化,也是代数式研究的基本思想的进一步发展. 以解决问题为出发点,设计适当的教学活动,引领学生经历用方程和不等式解决问题过程中符号抽象、运算和推理思想的操作体会、概括提炼、迁移应用、联系发展等过程,促进学生建立方程、不等式与代数式之间的知识及思想方法关联,发展学生的数学抽象、数学运算和逻辑推理等素养及问题解决能力.
关键词:方程不等式;专题复习教学;核心素养
方程和不等式是数与代数领域的核心内容之一,它既是数与代数式研究的自然发展,又与函数内容有着紧密的联系. 方程和不等式是初中数学最典型的模型之一,承载着数学建模解决现实问题能力的育人价值. 同时,方程和不等式又是教学中的重、难点,特别是难以根据问题情境建立方程和不等式模型. 用“符号抽象、推理和运算”这一“数与代数”领域的“大观念”引领,开展聚焦数学建模思想及符号抽象、推理和运算等关键能力的专题复习教学,对发展学生的数学抽象、逻辑推理、数学运算、数学建模等素养具有重要意义.
一、内容和内容解析
1. 内容
本节课是“数与代数”领域的专题复习,是聚焦用方程解决问题的符号抽象、推理和运算这一核心思想的概括提炼和迁移应用——通过符号抽象建立方程、不等式模型,用符号推理、运算解方程和不等式,并解决相关的实际问题.
2. 内容解析
在“数与代数”领域,首先通过字母表示数、列代数式表示数量与数量之间的关系,在此基础上研究两个代数式之间的大小关系,这是从代数式到方程、不等式发展的数学内在逻辑. 方程和不等式的学习,既是数与代数式学习的发展,也是函数学习的基础.
史宁中教授认为,抽象、推理和模型是三种最为基本的数学思想. 通过抽象把外部世界引入数学,形成数学的研究对象;通过推理,得到数学的命题和计算方法,促进数学内部的发展;通过模型,搭建数学与外部世界的桥梁. 数学抽象、推理和模型这三种数学基本思想在函数、方程和不等式中显得非常典型和连贯. 在实际问题中,有些数据不能通过直接测量确定,需要寻找相等或不等的数量关系,抽象出符号、建立已知数与未知数之间的联系,构建方程或不等式模型,借助运算和推理间接地得到数据,进而解决问题. 这是方程和不等式在解决问题中的独特作用,也是用方程和不等式解决问题的基本思想.
基于上述分析,确定本节课的教学重点为:以解决问题为载体,概括用方程和不等式解决问题的基本思想——符号抽象、推理和运算. 这与基础复习课中的“方程与不等式”复习教学的重点明显不同.
二、目标和目标解析
1. 目标
(1)通过具体问题解决及反思总结,能提炼出方程和不等式建模的基本思想和操作步骤.
(2)通过对解决问题过程的反思总结,提炼方程、不等式建模中的思想实质,即符号抽象、推理和运算,并总结其作用、操作步骤和要点.
(3)能应用提炼出的思想方法解决新情境中的问题.
2. 目标解析
达成目标(1)的标志:能用方程和不等式解决简单的实际问题,通过对解题过程的反思总结得到方程和不等式建模的思考框图和步骤要点.
达成目标(2)的标志:能发现建立方程、不等式模型思考过程的共性,通过归纳得到用方程、不等式解决问题的符号抽象、推理和运算的作用、步骤和要点.
达成目标(3)的标志:能在提炼出的思想和方法指導下解决新情境中的问题.
三、教学问题诊断分析
在基础复习阶段,数与式、方程与不等式复习的重点是:用数系扩充思想整理数的发展过程及相关知识;理解数的有关概念和法则;训练数学运算技能;用代数式表示数量关系;代数式的运算;方程和不等式模型的建立和解法. 学生会解方程,也会用方程或不等式解决简单的问题. 但学生还没有从“数与代数”领域的整体视野认识方程和不等式,理解其基本思想的一致性. 学习本课之前,学生已经学习了数学思想方法之符号抽象、运算与推理第1课时——数与式. 学生对这些数学思想方法已经不陌生,对符号抽象、推理与运算思想方法也已经有了初步的学习经验.
数学思想方法很抽象,学生更多的还是停留在只能意会不能言传的阶段. 本节课教学主要的困难体现在以下两个方面:一是在现实情境中如何抽象出符号,建立方程或不等式模型;二是总结符号抽象、推理与运算这种思想在应用方程或不等式解决问题过程中的作用、操作步骤和要点.
在解决实际问题时,列出方程和不等式既是重点也是难点. 例如,找等量或不等量关系对学生来说比较困难. 如果题目中已经说明,可以通过划关键词的方式在题目中找等量关系或不等关系;此外,有的相等或不等关系需要从现实生活中抽象、从科学情境中获悉、从数学公式中确定,这需要教师在教学中通过精选典型例题帮助学生积累经验. 再如,在找到等量关系后,怎样把这种等量关系转译成方程或不等式?这需要通过合理设未知数,用含有未知数的不同的代数式分别表示具有相等或不等关系的两个量. 这一表示过程中,首先要确定设什么量为未知数,其次要确定用哪些运算建立已知量和未知量之间的联系,列出代数式. 这需要对找到的相等或不等的两个量的组成结构进行分析,用代数运算加以表达,确定决定这两个量的构成要素是什么量,这个量就可以设为未知数,而构成的运算关系可以用来列代数式.
基于以上分析,确定本节课的教学难点为:理解设未知数、列方程与不等式过程中的要素分析和符号抽象方法.
四、教学过程设计
课前测试1:95%的酒精可用于擦拭紫外线灯;70% ~ 75%的酒精可用于消毒;40% ~ 50%的酒精可预防褥疮;25% ~ 50%的酒精可用于物理退热.
(1)现把75%的酒精与25%的酒精各取一部分进行混合,得到的酒精浓度范围是 ;
(2)如果要得到45%的酒精500 ml,则需要75%的酒精 ml,25%的酒精 ml;
(3)如果要得到40% ~ 50%的酒精100 ml,需要75%的酒精最多 ml,最少 ml.
答案与思路:(1)直观判断:浓度大于25%小于75%,这与“汤的浓度”问题相同;
(2)列一元一次方程或二元一次方程组,解得需要75%的酒精200 ml,25%的酒精300 ml;
(3)列不等式组可得需要75%的酒精最多50 ml,最少30 ml.
这三道小题反映了从粗略到精细的问题研究发展过程.
课前测试2:如图1,图1(1)的等臂天平呈平衡状态,其中左侧秤盘有一袋石头,右侧秤盘有一袋石头和2个质量为10 g的砝码. 将左侧袋中的一颗石头移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图1(2)所示. 被移动石头的质量为 .
答案与思路:列二元一次方程组或一元一次方程,解得被移动石头的质量为5 g.
课前测试3:某地猪肉的月平均价格从4月的50元 / kg涨到6月的60.5元 / kg,则平均每月涨价的百分比是 .
答案与思路:列一元二次方程,解得平均每月涨价10%.
1. 解决问题,感悟总结
前面我们学习过,通过字母表示数,列代数式及代数式的运算,可以解决课前测试1的第(1)小题. 我们接着进行思考.
问题1:课前测试1的第(2)小题是怎样解的?
师生活动:学生在平板电脑上递交解答过程,教师呈现学生的不同解法.
等量关系:混合前溶质的质量 = 混合后溶质的质量,混合前溶液的质量 = 混合后溶液的质量,质量分数 = [溶质的质量溶液的质量.]
追问1:为什么想到用方程解决问题?用方程解决问题的一般步骤有哪些?
追问2:用方程解决实际问题时,你是怎样想的?
追问3:需要怎样列方程?能与列代数式的过程进行比较,说一说列方程的思考步骤吗?
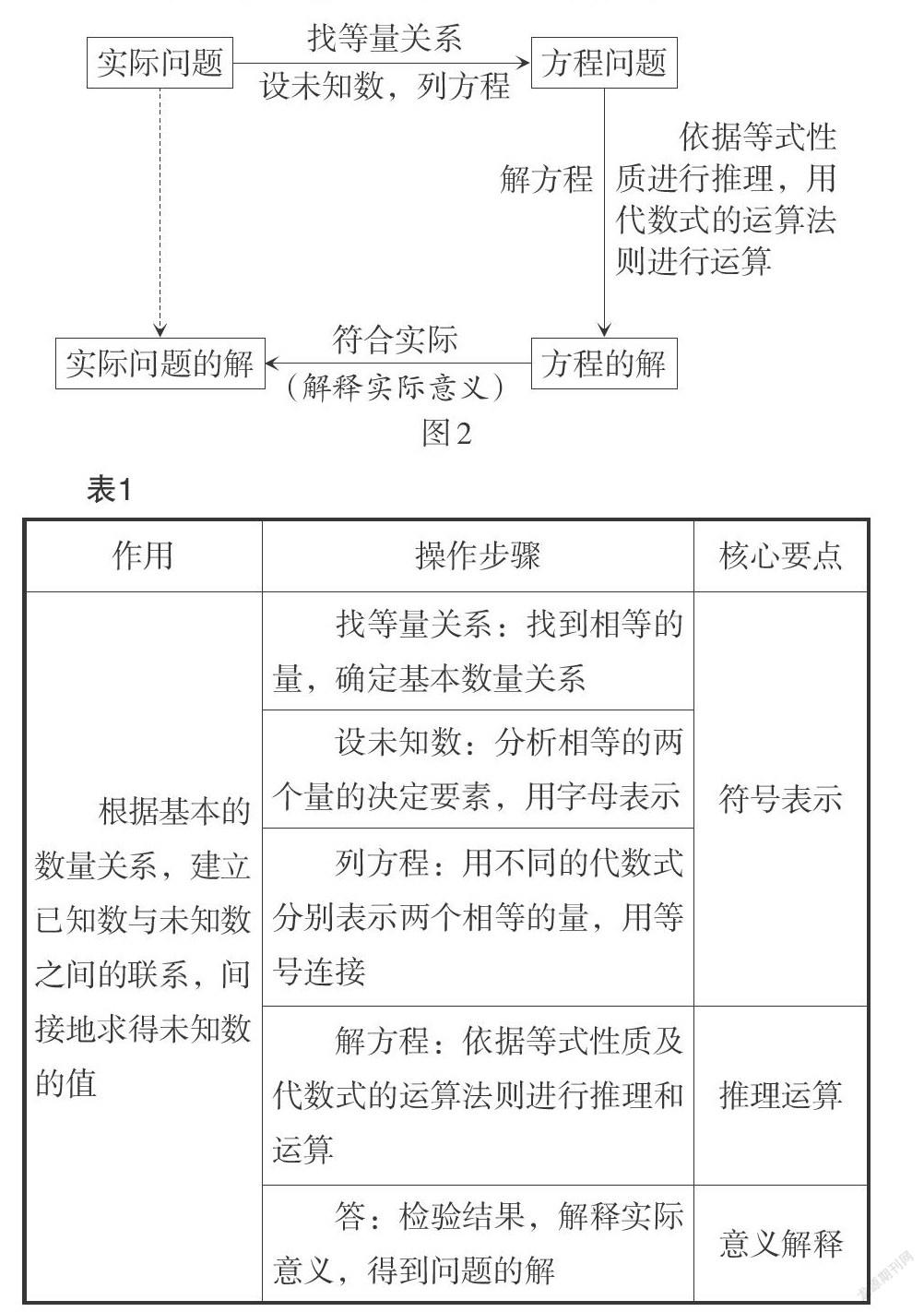
师生活动:通过师生之间的相互交流,总结列方程解决问题的一般步骤为“审、设、列、解、验、答”,概括出用方程解决问题的一般思路如图2所示,总结出方程建模的作用、步骤和要点如表1所示.
[表1][作用 操作步骤 核心要点 根据基本的数量关系,建立已知数与未知数之间的联系,间接地求得未知数的值 找等量关系:找到相等的量,确定基本数量关系 符号表示 设未知数:分析相等的两个量的决定要素,用字母表示 列方程:用不同的代数式分别表示两个相等的量,用等号连接 解方程:依据等式性质及代数式的运算法则进行推理和运算 推理运算 答:检验结果,解释实际意义,得到问题的解 意义解释 ]
【设计意图】通过用方程解决实际问题,让学生经历符号抽象、推理和运算过程,总结列方程解决问题的作用、步骤和要点.
问题2:课前测试1的第(3)小题是怎樣解的?
师生活动:学生在平板电脑上递交解答过程,教师呈现学生的解法.
不等关系:40% ≤ 混合后的酒精质量分数 ≤ 50%.
解:设需要75%的酒精x ml,则需要25%的酒精[100-x] ml.
答:需要75%的酒精最多50 ml,最少30 ml.
追问1:怎么想到用不等式解决问题?
追问2:用不等式解决问题时,你是怎样想的?
追问3:怎样列不等式,能与列代数式的过程进行比较,说一说列不等式的思考步骤吗?
师生活动:通过相互交流,总结列不等式解决问题的一般步骤为“审、设、列、解、验、答”,概括用不等式解决问题的一般思路如图3所示,总结不等式建模的作用、步骤和要点如表2所示.
[实际问题的解][实际问题][找不等关系][设未知数,列不等式][不等式问题][解不等式][ 依据不等式性质进行推理,用代数式的运算法则进行运算][不等式的解] [符合实际] [(解释实际意义)][图3]
[表2][作用 操作步骤 核心要点 根据基本的数量关系,建立已知数与未知数之间的联系,间接地求得未知数的取值范围 找不等量关系:找到不等的量,确定基本数量关系 符号表示 设未知数:分析不等的两个量的决定要素,用字母表示 列不等式:用不同的代数式分别表示两个不等的量,用不等号连接 解不等式:依据不等式的性质及代数式的运算法则进行推理和运算 推理运算 答:检验结果,解释实际意义,得到问题的解 意义解释 ]
【设计意图】类似于方程,通过用不等式解决实际问题,让学生经历符号抽象、推理和运算过程,总结列不等式解决问题的作用、步骤和要点,体会方程和不等式研究思想方法的相似性——符号抽象、推理和运算.
2. 归纳提炼,形成思想
问题3:通过前面两个问题的解决,能总结出用方程和不等式解决问题方法的共性吗?用方程和不等式解决问题的关键步骤有哪些?它和用代数式解决问题有什么联系?
师生活动:学生先独立思考,再小组合作,相互补充与完善. 教师小组内倾听,引导学生从方程和不等式有什么用、操作步骤是怎样的、核心要点是什么这三个方面归纳共性.
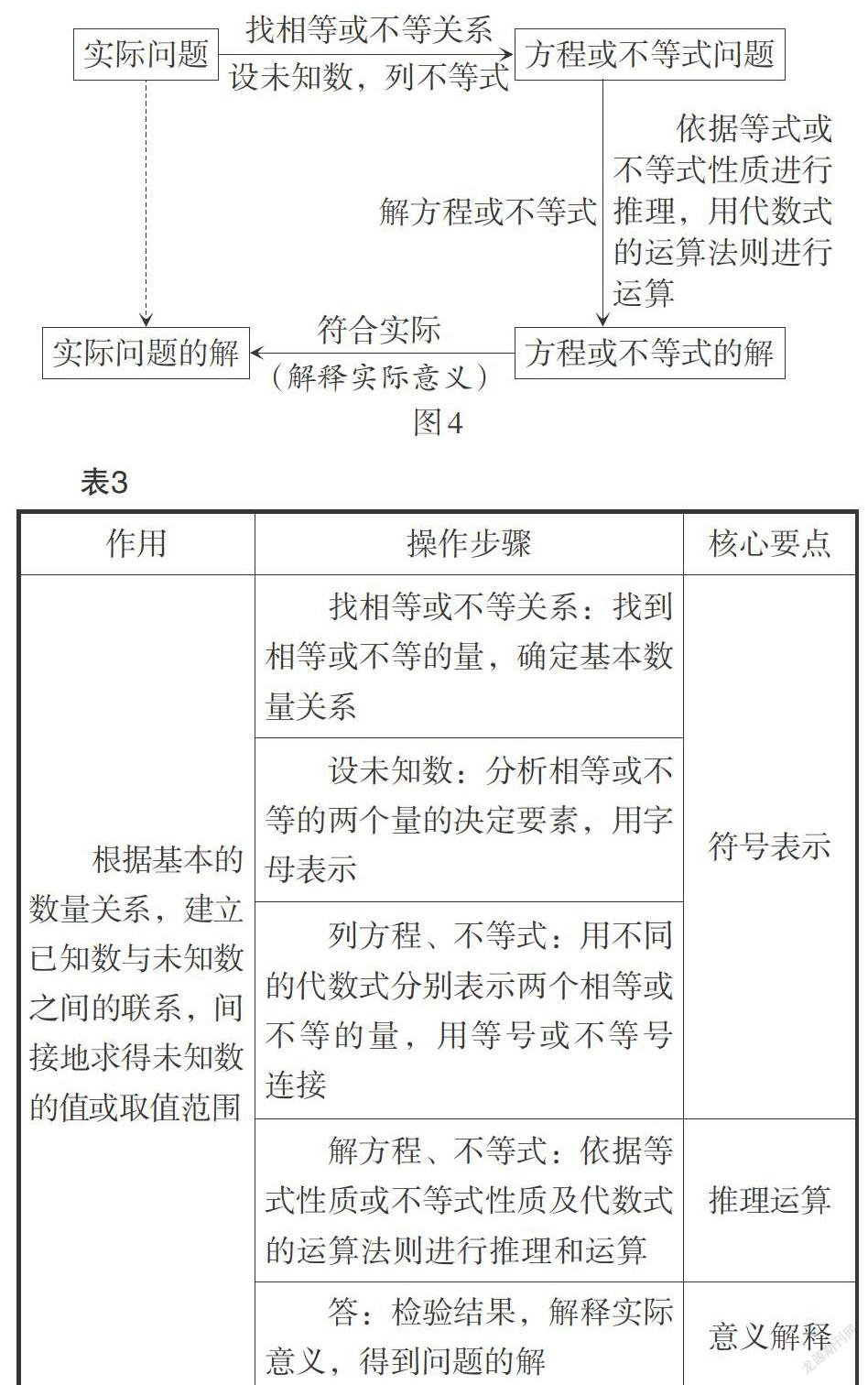
师生共同归纳得到如图4所示的框图和如表3所示的操作要领.
[实际问题的解][实际问题][找相等或不等关系][设未知数,列不等式][方程或不等式问题][解方程或不等式][ 依据等式或不等式性质进行推理,用代数式的运算法则进行运算][方程或不等式的解] [符合实际] [(解释实际意义)][图4]
[表3][作用 操作步骤 核心要点 根据基本的数量关系,建立已知数与未知数之间的联系,间接地求得未知数的值或取值范围 找相等或不等关系:找到相等或不等的量,确定基本数量关系 符号表示 设未知数:分析相等或不等的两个量的决定要素,用字母表示 列方程、不等式:用不同的代数式分别表示两个相等或不等的量,用等号或不等号连接 解方程、不等式:依据等式性质或不等式性质及代数式的运算法则进行推理和运算 推理运算 答:检验结果,解释实际意义,得到问题的解 意义解释 ]
【设计意图】通过两个不同背景的例子,分析解题过程,归纳解题过程中的共性和其中蕴涵的共同思想,发展学生的抽象、推理和运算能力;体会用方程或不等式解决實际问题的基本过程:基于用字母表示数,以代数式为工具,研究两个量之间的相等或不等关系. 这是从具体到抽象再到具体的过程,体会其中的关键是符号抽象、推理和运算,建立代数式、方程、不等式知识之间的关联性和基本思想的一致性.
3. 迁移应用,积累经验
问题4:课前测试2是怎么解的?
师生活动:学生先阐述自己的解题思路,教师观察学生的解题思路中是否用到了数学符号语言表达,是否有逻辑的运算,并进行适当地引导.
思路1:确定等量关系——左侧天平的增加量 = 右侧天平的增加量.
设被移动石头的质量为x g,则-x = -10 + x. 解得x = 5.
思路2:确定等量关系——左侧天平的质量 = 右侧天平的质量.
(1)设图1(1)左侧天平的一袋石头重a g,则右侧天平的一袋石头重[a-20] g. 设被移动石头的质量为x g. 由题意,得[a-x=a-20+10+x.] 解得x = 5.
(2)设图1(1)左侧天平的一袋石头重a g,右侧天平的一袋石头重b g,被移动石头的质量为x g.
【设计意图】此题着重引导学生通过要素分析合理地设未知数. 设未知数时,要分析具有相等关系的两个量各自的决定要素,用字母表示这个决定要素,在此基础上用不同的代数式分别表示这两个量,用等式表示两个量之间的相等关系.
4. 拓展提升,发展能力
例 洗一件衣服分去污和清洗两个阶段. 去污阶段:先把衣物放在含洗衣液的水中去污,让衣服中的污物充分溶解形成污水,拧干后衣服中还残留污水800 ml. 清洗阶段:加入若干清水清洗,充分混合后形成清洗水,再把清洗水拧干;再次加入清水清洗后又拧干;反复这样清洗,直到清洗干净(污水在清洗水中所占百分比为5%以下). 假设清洗阶段每次加入等量的清水,且每次拧干后衣服中残留清洗水800 ml.
在清洗阶段,如果想通过第二次加清水清洗后,使污水在清洗水中所占百分比在第一次基础上减少60%,每次应加入多少清水?
追问1:在解题的过程中,你会思考哪些问题帮助自己解决问题?
追问2:反思自己的解题过程,解决问题的关键步骤有哪些?
师生活动:学生先独立思考,遇到不理解的问题可前后桌之间相互解答,教师及时予以辅导.
基本的数量关系:质量分数 =[溶质质量溶液质量,] 溶液 = 溶质 + 溶剂.
第二次清洗后,原污水质量分数 =[1-60%]× 第一次清洗后原污水的质量分数.
设每次加清水x ml,则数量关系如表4所示.
经检验,[x=1 200]是原方程的解.
答:每次加入清水1 200 ml.
【设计意图】用学到的符号抽象、推理和运算思想建立模型,解决等量关系比较隐蔽的问题,深化学生对符号抽象、推理和运算等思想方法的认识,发展学生数学建模的能力.
5. 课堂小结,深化理解
(1)在用方程或不等式解决实际问题时,你是怎样想的?
(2)列方程或不等式时,有哪些思考步骤?
(3)解方程或不等式时是怎样想的?
(4)列方程或不等式的思考过程与列代数式有什么不同?有哪些联系?
师生活动:先由学生相互交流,再由师生共同归纳得到框图4和表3.
【设计意图】通过思考(1)引导学生整体回顾把实际问题转化为方程或不等式问题的整个建模过程. 通过思考(2)引导学生概括列方程或不等式的操作步骤,体会其中的符号抽象意识. 通过思考(3)使学生明确解方程或不等式,是依据等式或不等式的性质进行推理,用代数式的运算法则进行运算,这也是演绎推理的过程. 通过思考(4)让学生体会方程或不等式是以代数式为工具,研究两个量的相等或不等关系,是从具体到抽象再到具体的过程,而代数式是借助字母表示数,从特殊推广到一般的思考过程,建立数、代数式、方程、不等式之间联系,建构有序、多级的知识体系.
6. 课后目标检测
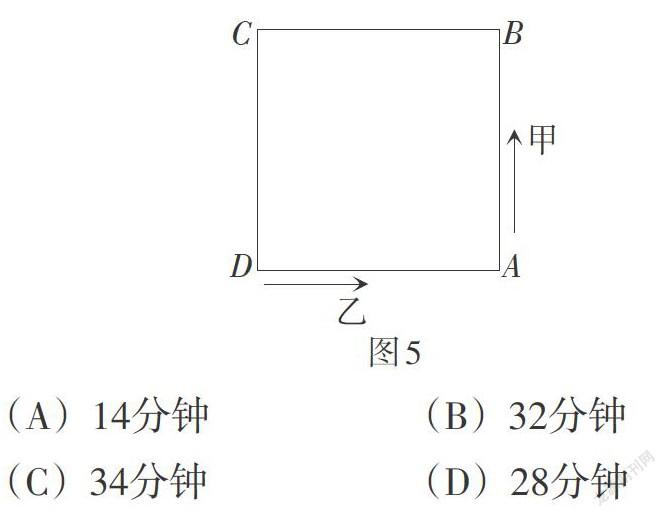
(1)甲、乙两人在广场上绕水池边散步. 如图5,已知该正方形水池的周长为400米,他们在相邻的两个角上同时沿池边逆时针行走,乙在甲后,甲每分钟走50米,乙每分钟走44米,那么甲乙二人自出发后到初次在同一边上行走所需要的时间是( ).
(A)14分钟 (B)32分钟
(C)34分钟 (D)28分钟
(2)某广告公司招标了一批灯箱加工工程,需要在规定时间内加工1 400个灯箱,该公司按一定速度加工5天后,发现按此速度加工下去会延期10天完工,于是又抽调了一批工人投入灯箱加工,使工作效率提高了50%,结果如期完成工作. 求该公司前5天每天加工多少个灯箱?
(3)从盛满20升纯酒精的容器中倒出若干升,然后用水注满,再倒出同样升数的混合液后,这时容器里剩下约5升纯酒精,问每次倒出多少升溶液?
(4)一个自行车的新轮胎,若把它安装在前轮,则自行车行驶5 000千米后报废;若把它安装在后轮,则自行车行驶3 000千米后报废. 行驶一定路程后可以交换前、后轮胎. 如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶多少千米?
五、教学设计中的若干思考
1. 用“数与代数”领域的大观念引领,聚焦核心思想进行整体教学,发展学生的数学学科核心素养
在初中数学课程中,“数与代数”“图形与几何”“统计与概率”等领域各有自身的大观念和核心思想. “数与代数”领域的核心思想是符号抽象、推理与运算,其大观念是通过符号抽象,建立代数式、方程、不等式、函数模型,通过代数运算和推理,研究数量的大小、数量关系及其规律(在运算中的不变性). 抓住这一核心思想组织本领域的专题复习教学,可以促进学生体会本领域的大观念,领会本领域蕴涵的核心思想和方法,用整体视角建立起本领域有序、多级的知识体系,实现“數与代数”领域发展学生的符号抽象及其推理和运算等关键能力的育人价值.
本节课的教学设计中,课前测试1的第(1)小题是衔接上一节课“符号抽象、推理和运算(1)——数与式”专题复习的,通过对浓度的简单混合到定量混合得到目标浓度的问题深化研究,引导学生从代数式研究过渡到方程与不等式的复习,体会方程与不等式是基于大小关系研究到代数式研究的自然发展,暗示学生本节课同样要用“符号抽象、推理和运算”复习用方程与不等式解决问题的思想和方法.
2. 遵循数学思想方法和活动经验的学习规律,设计操作体会、反思总结、迁移应用等教学环节
数学思想方法和活动经验的学习需要经历操作体会、明朗化、迁移应用和联系发展等阶段. 本节课的教学设计了“解决问题、感悟总结;归纳提炼、形成思想;迁移应用、积累经验;拓展提升、发展能力;课堂小结、深化理解”等教学环节,以具体、典型的问题解决为载体,抓住反思总结这一关键,遵循数学思想方法和活动经验的学习规律进行教学,教学活动和教学内容与教学目标相匹配,与学生的学习规律相适应,从学生的课堂反映也可以看出学生的思考和表达是有序发展的.
3. 设计有针对性的问题,形成可操作的方法,帮助学生突破难点
在列方程和不等式解决问题的过程中,难点是“列”,列方程和不等式难在哪里?难点主要有两个方面:一是找不到相等或不等关系;二是即使找到了相等或不等关系,却难以将其转化为方程或不等式.
对于难点一,考虑到等量关系存在的四种典型方式:(1)问题中直接给出;(2)从生活经验中抽象;(3)从自然科学中获悉;(4)从数学定理公式中提取,故对这个难点的突破是用典型例题来实现的. 例如,课前测试的三道小题可以根据科学原理找等量关系,例题是根据生活经验结合科学原理找等量关系. 由于教学时间的限制,没有设计数学内部用方程和不等式解决的问题,这是今后教学中要改进的.
对于难点二,通过引导学生对相等或不等的两个量的组成进行分析,分析其决定和构成要素,用未知数表示构成要素,通过已知数和未知数间的代数运算,建立不同的代数式分别表示相等或不等的两个量,最后用等号或不等号连接表示这两个量的代数式,得到方程或不等式,这一过程是以要素分析为基础,抽象出符号的过程. 而后面的解方程或解不等式,则是依据等式或不等式的性质、代数式的运算法则进行推理和运算的过程. 通过这种突破难点的教学设计,把“符号抽象”的过程体现得更加具体、深刻,也使突破难点有了可操作、有针对性的方法,还可以让学生理解“列方程以列代数式为基础”的含义. 本节课中,是在用方程或不等式解决问题后及归纳提炼中,用追问“怎样列方程(不等式),能比较列代数式说说列方程(不等式)的思考步骤吗?”来实现的.
4. 基于测评进行教学
上述教学设计还体现了基于测评进行教学的思想. 通过课前测试了解学情,提出本节课的教学问题,基于学情进行适当教学,通过课后测试评价教学效果. 例如,根据课前测试2的反馈,发现多数学生是用文字语言表述自己判断的过程,如10 g砝码就是被移动的石块的质量2倍;左侧天平减少的量就是被移动的石块的质量,右侧天平减少的量是10 g砝码的质量减去被移动的石块的质量等. 学生缺乏自觉应用符号进行推理的意识. 在课堂教学中,教师有针对性地进行点拨与提升,引导学生反思自己的思考过程,在与同伴的交流中,形成多样的符号表达,发展符号意识.
总之,只有遵循知识发展的逻辑规律,合理构建知识体系,精心选题,通过对不同背景的问题进行分析,提炼解决问题的一般规律,让学生学会洞察本质的一致性,领悟数学思想方法,并用学到的思想方法解决问题,发展问题解决能力,才能真正落实“四基”、发展“四能”. 这就要求我们深入研究和理解数学、理解学生、理解技术、理解教学,通过适当的设问,用程序步骤等形式,把数学基本思想、活动经验等进行显性化呈现,让学生学会思考问题,形成解决问题的策略和方法.
参考文献:
[1]史宁中. 数学思想概论(第1辑):数量与数量关系的抽象[M]. 长春:东北师范大学出版社,2008.
[2]吴增生. 数学思想方法及其教学策略初探[J]. 数学教育学报,2014,23(6):11-15.
[3]吴增生. 科学用脑高效复习:初中数学总复习教学设计[M]. 杭州:浙江科学技术出版社,2018.
[4]章建跃. 章建跃数学教育随想录[M]. 杭州:浙江教育出版社,2017.
[5]教育部基础教育课程教材专家工作委员会. 《义务教育数学课程标准(2011年版)》解读[M]. 北京:北京师范大学出版社,2012.

