再现原创性思维，体验“真实”发现历程——数学再发现教学设计示例

湖北省赤壁市第一初级中学(437300)李道生

湖北省赤壁市蒲圻初级中学(437300)刘国胜

湖北省赤壁市实验中学(437300)石小东

1 问题提出背景

科学上许多定理公式定律的发现,对现在的我们而言,已无从知晓科学家当初真实的发现历程,但追溯定理公式定律的发现历程,重新探讨发现之路,对培养学生创新能力是极为重要的途径;我们不应满足定理公式结果的传授,更应注重知识探索的发现过程.每个定理公式不同的分析思路可能有不同的发现方法,我们应尽可能多的寻找不同的发现方法,并引导学生比较其中最合乎思维规律最科学自然的发现之路,这才是数学教学价值所在.由此设想,当初科学家如若按此最合乎思维规律最科学自然的发现之路去分析思考,一定会少走弯路,直接快速发现相应的定理公式.不断总结最佳的发现之路,优化思维方法,是提高自我创新发现能力的重要方式,数学教学更应如此挖掘深化,这比简单做几道所谓的难题更有意义.

展现数学真实发现历程的“真实”,不一定是数学家当初真正的发现历程,但一定是符合思维规律的发现历程,可另行独立发现之路的发现方法;科学上不是常有不同科学家各自独立发现同一数学规律方法的现象吗?我们的教学设计也应在学生不知晓所学定理公式定律的前提下去重新探索独立发现它,这是设计教学程序引导学生进行探索性思维活动所应注意的首要问题,使学生提出和发现问题成为必然,而不是“撞大运”.

教材给出的数学体系是一门系统的演绎科学,它直接给出发现的结果而隐去了发现的过程,可是这种发现过程可以加深对知识的理解和记忆,特别是可以有效地发展创新思维能力.因此,如何从数学思维的结果出发,回溯数学发现思维过程,就成为设计教学程序的一个重要课题.

再次强调的是,这里所指的发现数学结论的思维过程,不是指数学家当年真实的发现过程,而是指合乎数学思维规律,适合学生思维水平与知识水平的经过教师加工的发现过程,称之为“再发现过程”.

2 再发现教学情景展现

下面将“圆面积公式”再发现过程的教学设计及实施过程以师生对话的形式表述如下,具体说明数学发现的一般思维过程及如何设计再发现教学程序引导学生进行探索性思维活动.

教师:圆面积公式这是大家早已熟悉的,但它是怎样发现的?你能发现它吗?

学生:小学我们学过圆面积公式的发现方法:将圆分成若干等份,再拼接成近似矩形,即可由矩形面积公式S=ab发现圆面积公式S=πR2.

教师:对,这里运用“转化”的思想,通过分割、拼接,将未知面积公式的圆转化为已知面积公式的矩形,由此发现圆面积公式.其过程为:

图1

分析以上过程,我们会问:数学家怎么会想到将圆分成2n等份(而不是2n+1 等份)?又怎么会想到将此2n等份按两个半圆(各n等份)展开、对接?既然如此思维过程不是我等“凡夫俗子”所能想到的,难道说数学家是“天子下凡”,具有超凡的思维能力?当然不是,实际上,如此“发现过程”并不是数学家真实的思维过程,而是“事后诸葛亮”之辈,人为设计的一种所谓“发现式教学程序”,充其量只能算作检验(或解释说明)圆面积公式正确性的一种实验方法.

评注如此“发现式教学程序”并不能真正培养学生的数学发现思维能力,如此类似的有:发现“三角形内角和定理”的所谓“剪拼法”;发现“勾股定理”的所谓“度量法”等.

教师:假设大家从未见过圆面积公式,你能设计一套自然流畅的符合我们“常人”思维的发现方法吗?

学生:……

教师:如果你不能发现圆面积计算方法,那么你能发现其一部分面积的计算方法吗?

学生:……

教师:什么是圆的一部分?怎样得到圆的一部分?

学生:啊!分割!作半径可将圆分割成若干部分.

教师:你能求出分割后每一部分的面积吗?

学生:……

教师:观察分割后每一部分的结构形态,再试试看.

学生:对了!分割后每一部分近似三角形,我们可借助三角形面积公式来计算圆的每一部分的面积.

教师:很好!请计算一下.

教师:反思一下小学发现圆面积公式的操作过程:分割→展开→拼接.现在看来完全是画蛇添足;既然分割后的每一部分近似于三角形,那么,直接由三角形面积公式发现圆面积公式岂不更快,何必舍近求远,硬要拼接成近似矩形,再由矩形面积公式去发现圆的面积公式呢?

另外,由于分割后的图形是“近似”三角形,故由此所发现的圆面积公式也给我们一种“近似”的感觉,究竟是否是真正的圆面积公式,我们仍心存芥蒂没有把握.正确与否,最终要经过严格的逻辑证明才能确定.不过,在证明之前,倘若我们还能采用其它方法发现同样形式的圆面积公式,则我们会更进一步相信所获发现的正确性,再行证明就不会做徒劳之功.

图2

你还能用其它方法发现它吗?

学生:……

教师:你还有其它方法获得圆的一部分吗?你见过其它形式的圆的一部分吗?

学生:对了,圆环!在小学六年级的数学习题中经常见到这类图形.

教师:对,圆环是圆挖去一个同心小圆后的剩余部分,现在的问题是,若发现了圆环面积的计算公式,就能由此发现圆面积的计箅公式吗?

学生:能,因为当圆环的内圆缩成一点时,圆环就变成了圆,也就是说,圆可看成是内圆周长为零的圆环.因此,发现了圆环面积的计算公式也就同时发现了圆的面积计算公式.

教师:好!你能发现圆环面积的计算公式吗?

学生:……

教师:请大家仔细观察圆环结构特征,看从中有何启发.

学生:圆环中间的宽度处处一样.(见图3)

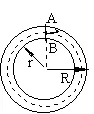
图3

教师:非常重要,这一特征你能产生什么联想,

你能发现其面积吗?

学生:我发现了!圆环的面积应等于中间的宽度AB乘以它扫过一周所扫过的周长C,C应取正中间那一个圆的周长.即

教师:你能解释一下,你作出这一猜想的理由吗?

学生:说不清楚,但我总感到只有这样计算才合理些.

教师:大家能帮助他把理由讲清楚吗?

学生:……

教师:我们知道,丙同学是在看到圆环的特征——中间宽度处处相同的前提下,作出猜想的,大家能由此帮他作出解释吗?

学生:……

教师:什么图形与圆环有类似特征?

学生:平行线,

教师:对,平行线中间距离处处相等;由此马上使我们产生类比联想,AB绕圆环一周,正好相当于AB沿平行线l1、l2扫过一段路程a(见上图4 所示),而后者的面积为AB乘以扫过的路程a.于是会想到:圆环的面积应为AB乘以沿圆环扫过一周的周长C,这应是他作出如上猜想的原因.至于如何想到取正中间那一个圆的周长,那即是“平均”思想作用的结果.

图4

经过刚才的分析,大家还有什么想法?

学生:老师,圆环中间宽度不变,但内外周长不同,正好类似于梯形特征——梯形上下底平行,从而中间等距,但上下底长不同.由此我想,将圆环看作一个梯形,上底长为内圆周长C内,下底长为外圆周长C外,高为圆环宽度AB(AB=R-r),则可借助梯形面积公式发现圆环面积公式(见图5).

图5

教师:很妙,计算一下试试看.

学生:

学生:令r=0,则圆环内圆缩成一点,圆环变成半径为R的“整”圆,于是,我们又可发现半径为R的圆面积公式:

教师:对!这里,我们又一次感受到类比发现的重大功能,从圆环与梯形的结构特征相似,联想到其面积的计算方法应有相似性,这一重要的思维方法在科学研究中经常发挥重要的作用,大家应细心体会,认真掌握.

以上类比发现过程可图示如下:

图6

评注与前面相比,这里所采用的类比发现法更具理性成份,想法更高明,结论更可靠.如果说前面的发现法为实验操作法(具有直观近似性的特点),则后者可视为理性分析法(具有抽象精确性的特点),由此设计的再发现教学程序更利于培养学生的创造性思维能力,我们应鼓励如此形式的再发现教学程序的设计方法.

教师:大家还有什么见解,尽管表述,不要受我的支配.

学生:上面的发现启发我,若将圆环沿AB剪开,再朝相反方向均匀拉伸,且不改变中间宽度,那么圆环就变成了一个等腰梯形.有些书上说圆环不能展开,这里怎么展开了呢?

教师:问得好!敢于质疑,这正是科学发现的重要条件之一.但你注意到没有,剪开圆环的地方在变为梯形的腰后长度增加了(见上图5).

学生:这样看来,还是不能展开.

教师:对,虽然如此,但从圆环与梯形的结构特征相似方面看,可以说,你将圆环“理想化”地“展成”了梯形.

学生:老师,我有一个问题,如果认为圆环能“理想化”地“展成”梯形,那么我想:圆环之间的每一个内圆周相应地展直为梯形两底之间的一条与底平行的线段,从而两者之间应有一一对应相等的关系.只有这样,我才认为圆环能“展成”梯形,才感到“展开”的梯形面积与圆环的面积相等,否则,我将怀疑上述发现的正确性.

教师:你上来计算一下试试看.

学生:如图7,取圆环之间的任一内圆周,设半径为r+h(0 ≤h≤R-r),则其周长为2π(r+h)

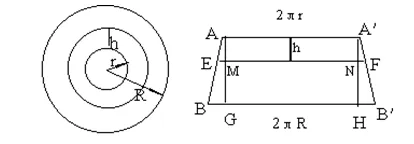
图7

真巧,完全相同,我不怀疑了.

学生:老师,这里启发我作出这一猜想:“两平面图形,若能建立线段之间的一一对应相等关系,那么这两个图形的面积相等”.

教师:大家对他的猜想的正确性有何看法?

学生:凭直觉好象是这么回事.

教师:请大家观察右图8,看一下以下推导过程:在ΔABC中,令AC ＞BC,CD⊥AB,很明显,ΔACD的面积要大于ΔCBD的面积,然而,对于AB的任一条平行线FG而言,如果分别由F、G两点来作AB的垂线段FH和GJ,则都有FH=GJ,这种对应关系是普遍存在的.换句话说,无论在ΔACD中选择哪一条垂线段,都可以在ΔCBD中找出一条垂线段与之相等,反之亦然.既然ΔACD与ΔCBD都是由各自的垂线段组合而成,而它们的垂线段之间又有一一对应相等的关系,那么照上同学的猜想,这两个三角形的面积应该相等了,这显然与事实不符.

图8

学生:真不可思议.

教师:可见,凭直觉的发现并不完全可靠,只有经过实践检验或严格的证明,才能断定发现的真伪.

大家还有什么见解,请畅所欲言,各抒己见.

学生:老师,我们已经知道圆环可看作是“理想化”的等腰梯形;我想:圆作为内圆周长为零的圆环,应可看作是上底为零的等腰梯形——等腰三角形.其底边长为圆的周长2πR,高为圆的半径R,由此,可直接发现圆的面积公式.即.

学生:老师,前面你介绍了类比发现的重要作用,圆与球作为平面与空间的一对对应图形,我们应可对照圆面积公式的发现方法发现球体积公式,……

教师:妙?继续讲.

学生:根据圆对应一个等积的“等腰三角形”,底为圆的周长,高为圆的半径,则球应对应一个等积的“等腰圆锥”,底面为球的表面,高为球的半径.其间的对应变化关系可图示如下:

图9

教师:这里,我们又一次看到类比发现的伟大功能,历史上,人们对球体积公式的发现,经历了复杂曲折的过程,这里,被大家轻而易举地发现了.可见,科学的思维方法是进行科学研究获得发现的锐利武器,大家一定要切实掌握好.

3 再发现教学程序特征总结

纵观圆面积公式发现过程的“对话”,我们看到,设计再发现教学程序,引导学生进行探索性思维活动时,必须注意以下几个问题:

第一,教师亲自体验定理、公式的探索过程,以便凭自己直接真实的感受,制订出符合思维规律的教学程序.

第二,设计教学程序,应充分暴露数学发现的思维过程,不掩盖数学思维的任何一个环节,充分揭示知识的发展过程.

第三,在引导学生进行探索性思维活动时,应控制学生的思维朝正确的方向发展,但又可以不受拘束地自由交换意见.互相启发,互相补充,克服力所能及的困难.最大限度地调动学生的主动性和积极性.

第四,再发现方案,要顺其自然,合乎情理,不能为了发现而发现,要让学生成为探索者,而不要把学生看成是老师的工具,为此,要做到:(1)不要回避“发现”的失败,相反地,应该体现出发现的曲折过程,让学生从成功与失败的比较中受到教益.(2)要因势利导,不要强行推行教师的预定方案,必要时要放弃预定方案,顺着学生的思路前进.

第五,由于发现思维往往表现为顿悟和灵感,是分析思维的高度简约,有时连发现者本身也不明了这个简约的过程,有讲不清发现过程的现象但是作为教学过程我们不应的停留在这种认识上,因为这样做,不可能有效地培养学生的思维能力,特别是直觉思维本身,这样做实际上是掩盖了数学思维的某些环节,我们必须对数学思维的某些环节作慢镜头的解剖,找出被它简约的环节,为直觉发现的产生铺设一条逻辑通道.

第六,通过探索得到某种结论固然重要,但我们更着重于总结获得这种结论的思维规律.

总的说来,数学教师是通过自己的创造性思维活动,指导调控学生的思维活动,使学生的思维活动与成功的数学思维活动“同步”,以重新获得数学家的数学思维已经取得的成果,并通过的这个过程,逐步实现数学思维结构向数学家思维结构的转化,最终达到提高学生创造性思维活动的目的.