如何让学生想到将圆等分成扇形来推导圆面积公式

邵虹

教学圆面积公式推导时，需要将圆等分成扇形来研究，教师可以采用以下教学过程。

一、回忆平行四边形面积公式的推导

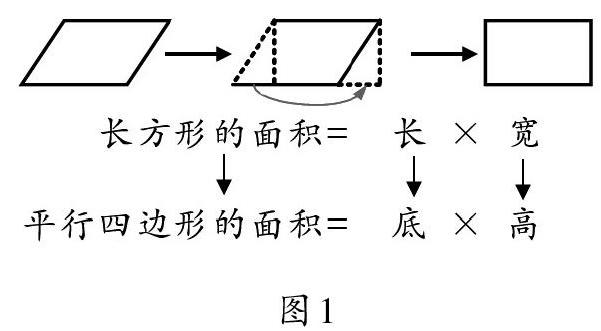
PPT演示（如图1），启发学生回忆平行四边形面积公式推导的过程。

预设学生回答：将平行四边形通过割补，转化成已经掌握面积计算公式的长方形，找到平行四边形的底、高与长方形的长、宽之间的联系，最终得出剪拼后的长方形面积等于原来平行四边形的面积，这就是“转化思想”。

二、将圆转化成已经学过的平面图形

用转化的方法，可以把没学过的知识转化成已学过的知识。那么，探究圆面积的计算公式，可以转化成哪些平面图形呢？预设学生回答：已经学过并掌握面积计算公式的图形有长方形、正方形、平行四边形、三角形和梯形。圆面积计算公式推导时，可以转化成这些图形。

三、将圆等分成扇形探究圆面积公式

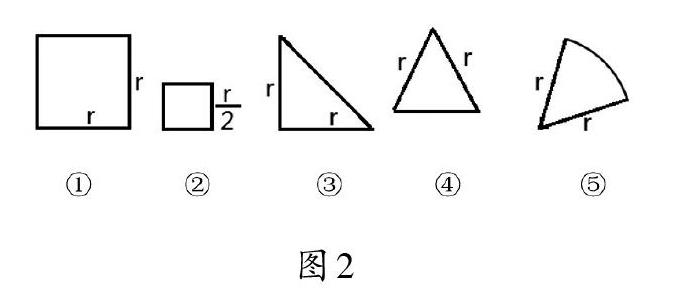
圆是不是也可以通过割补，转化成平行四边形、长方形等图形来探究面积计算公式呢？圆分割成什么图形，有利于圆面积公式的探究呢？请学生从下列图形中，选择一种来研究（如圖2）。

1.如果选择图形①或图形②，可以帮助学生通过数正方形个数的方法，度量得出圆面积的大致取值范围，但不能得出精确的结果，较难推导圆面积计算公式（如图3、图4）。

2.如果选择图形③或图形④，会得到一个正多边形。也可以通过三角形面积之和来估计圆面积的大小，但是存在一定的面积差（如图5、图6）。

3.如果将圆分割成图形⑤（扇形），作为研究圆面积公式的基本图形，可以发现扇形能够将圆完全等分，没有面积差。扇形既是圆的一部分，又与三角形十分相似，而且等分后的扇形弧长总和是圆周长，两条直边是圆的半径，这些要素对推导圆面积公式十分有利（如图7）。

通过以上观察、比较、想象与分析，学生得出将圆等分成扇形，有利于圆面积公式的研究与推导。

（浙江省杭州市上城区教育学院   310002）