小学数学教学中的一些说法(一)
汪一敏
在小学数学教学中,常有一些说法似是而非,甚至错误。数学教师对此须有清晰的认识,才能更好地进行教学。
一、一般的平行四边形不是轴对称图形
平行四边形是不是轴对称图形?不少教师还是有疑惑的。有些教师接受了平行四边形不是轴对称图形的观点,在教学中通过让学生对一般的平行四边形进行探索(观察折叠等),从而得到平行四边形不是轴对称图形的结论。但有些教师注意到特殊的平行四边形是轴对称图形,如菱形。
我们在进行判断推理时要用到概念,概念可以指向个体(概念中的元素),也可以指向整体(概念元素的集合)。如“人”,在说理的过程中它是指个体,还是指整体,有时真会把人搞糊涂,所以为了明确地表达观点,在“人”用于表达集合概念时,会用“人类”一词。
但汉语中表达概念的词有这种特性的不多,“白马非马”之所以能把许多人绕晕,就是因为“马”既可以指向个体(具体的马),也可以指向整体(马的集合)。公孙龙牵着白马来到城门前,守城士兵说“马不能进城”,公孙龙说“我的白马不是‘马”……这里士兵所说的“马”是指个体,而公孙龙所说的“马”是指整体(集合概念)。从逻辑上而言,公孙龙的“诡辩”也没有錯,守城士兵无法反驳他,所以让他牵马进城了。
对小学生来说,要理解“白马非马”中的逻辑关系有点困难,因为他们难以理解集合概念的含义。通常他们在使用概念时,往往指向概念所属的个体,从这个意义上说,“平行四边形不是轴对称图形”的说法是不对的,因为平行四边形中的菱形(包括正方形)是轴对称图形。
当我们把“平行四边形”作为单个数学对象即作为集合概念看待时,“平行四边形不是轴对称图形”的说法也没错,就像“白马非马”,这时上课的过程就不是通常所见的了。
当教师理解、清晰了这其中的逻辑关系,就会选择结论:“一般的平行四边形不是轴对称图形。”并在课堂教学中有相应的体现。
二、面动成体的说法极不严谨
点、(直)线、(平)面是几何学的基本元素,这种被抽象了的理想化元素的特点是点没有大小,线没有粗细,面没有厚薄。那种联系长方形说“线”没有宽度、联系长方体说“面”没有高度的表述,既不恰当,也无必要。
点、线、面这种理想化的特征,小学生理解起来有点困难。当年虚数(复数)产生时,曾引起人们的不解和焦虑:它表示什么?如何理解?直到高斯用复平面解释说,一个虚数(复数)表示复平面上的一个向量,才消除了人们的焦虑。用数学模型表征数学概念,可加深学生对数学概念的理解。当学生疑惑地提出:“老师,那么有没有粗细的线?”你可以这样回答:“我画一条给你看看。”(见右图)
图中黑白交界的线没有粗细。两条没有粗细的线的交点没有大小。
为了把点、线、面联系起来,有些教师认为“点动成线,线动成面,面动成体”,并由此展开课堂教学。虽然在课堂氛围中,师生对“动”的理解并无歧义,“动”即平移,但写成文章,这种说法十分不妥。比如点动成圆也是“动”,圆绕其一条直径旋转一周也是“动”,但结果是球。
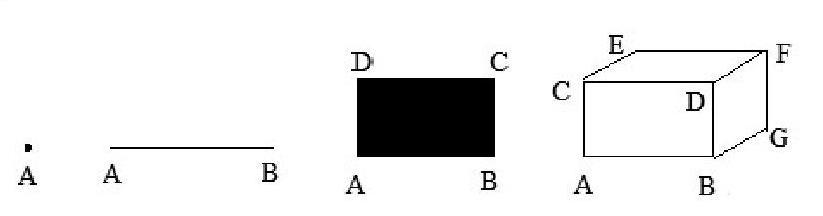
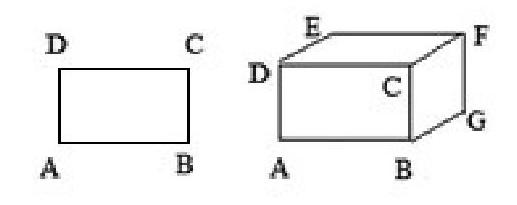
点平移成线,线平移成面。有些教师在教学中是这样诠释“点动成线,线动成面,面动成体”的,见下图。
点A平移成线(段)AB,AB可以平移成长方形面ABCD,长方形面ABCD可以平移成长方体。
是长方体吗?不是!长方体内部是“空”的,而平移出来的这个“长方体”是实心的。
有的教师则简单一点,只想用动的观点来说明长方形与长方体的联系(见下图)。
长方形(垂直)平移一段距离,形成长方体。结果这个“长方体”只有四个面,面ABCD与它的相对的面是没有的。
因此,“面动成体”的说法极不严谨。
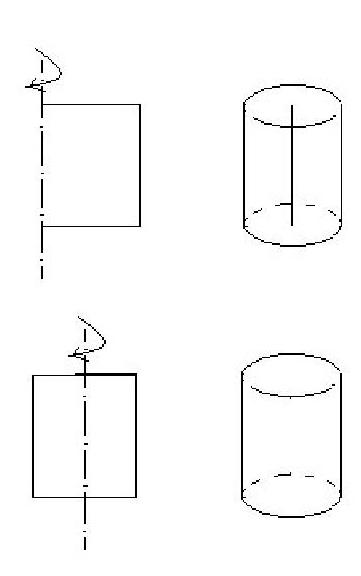
类似的错误在各类教科书中也有出现。如“长方形绕其一条边旋转一周得到的图形是圆柱”(见右图)。
这两底面圆心有一连线的几何体是圆柱吗?
正确的应该是“长方形绕其一条对称轴旋转一周得到的图形是圆柱”。
(杭州师范大学教育学院 310000)

