看“一”的眼光
郜舒竹
【摘 要】数学课程内容中,除了有客观、统一和确定的标准单位,相对于人的认知过程,还有主观、个性和多样的意念单位。许多内容的理解都与意念单位的选择、使用、分解、组合、转化有关。看“一”的眼光,指的是对“一”的选择和使用。这种单位化的眼光对于建立数学课程内容之间的联系以及解决问题过程中方法的生成,都会起到重要的作用。不仅如此,单位化作为一种认知能力,也是数学课程内容中所蕴含着的育人因素。数学教学应当让学生亲力亲为地经历这样的认知过程,发展认知能力,实现数学的教育性。
【关键词】单位;标准单位;意念单位;认知能力
“一”也叫“单位(Unit)”,数学课程中许多内容都与单位的选择、使用、分解、组合、转化有关。看“一”的眼光,指的是对单位的选择和使用。作为人的认知能力,这种眼光对于建立数学课程内容之间的联系以及解决问题过程中方法的原创生成,都会起到重要作用。
一、什么是“单位”
通常的数学课程与教学中,会把“一,十,百,千……”叫作十进制记数法的“计数单位”或“记数单位”;把小数中的“0.1,0.01,0.001……”叫作小数单位;把“[12],[13],[14]……”这样分子是1的分数叫作“分数单位”;把“米,厘米,毫米……”叫作长度单位,诸如此类用于量的“度量(Measurement)”,还有面积单位、体积单位、角的度量单位、质量(重量)单位、时间单位、货币单位、温度单位,等等。
这样的单位具有相对“客观、统一、确定”的特点。“客观”指的是外在于学习者的主观意愿;“统一”指的是长期以来人们的普遍公认并且约定俗成,遵循这样统一的标准,可以实现尽人皆知、没有歧义的表达。正是这样的客观性和统一性使得单位具有了约定俗成的“确定性”,不会依据人的主观意愿进行改变。因此,这种单位实质是一种具有普遍意义并且约定俗成的语言,是实现表达和交流的工具。这种具有客观性、统一性和确定性的单位可以称之为“标准单位(Standard Units)”。
从认知的角度看,单位实质是人对待“一”的看法和想法,有了“一”,才能使得“几”或“多少”具有确定的意义。如果把看待和选择“一”的过程视为人的主观行为或思维过程,这样的过程也叫作“单位化(Unitizing)”,是人的一种认知方式,也可以认为是人的一种认知能力,具有主观、个性和多样的特点。
正如古希腊欧几里得在《原本》中把“单位”定义为“每件事都是单位”[1],而表达多少的数(自然数)是单位的复合。比如通常所说的“6个苹果”,是把“1个苹果”视为“一”。如果改变对“一”的看法,把“2个苹果”视为“一”,那么“6”这个数就变为“3”,6个苹果的说法就变为“3对苹果”。再比如“6根筷子”中的“6”是将“1根筷子”看作“一”。如果改变看法,把“2根筷子”视为“一”,那么“6根筷子”的说法就变成“3双筷子”。原本用数“6”表达的对象,改变为用数“3”来表达。
因此可以说,用于表达“几”的数,是相对于“一”而言的,看待“一”的眼光,决定了用哪个数表示“几”。因此数是人头脑中建构的概念,属于抽象的范畴。
更进一步,还可以把“6个苹果”这个整体视为“一”,这时其中的“1个苹果”就需要用分数“[16]”来表达,其中的“2个苹果”就变为“[26]”。如果把“2个苹果”看作“1对苹果”,那么“6个苹果”的表达就变为“3对苹果”,同样把“3对苹果”视为“一”,这时“1对苹果”(2个苹果)的表达就成为分数“[13]”。这样用变化的眼光看待单位的过程,体现了“[26]=[13]”的意义,也就是分数中“约分”的过程,小学数学课程内容中也叫作“分数基本性质”。
按照这样的理解,单位实质是人与环境互动中,对客观对象生成看法和想法过程中的产物,是思维中形成的对象或实体(Conceptual Entity),是人主观生成或“建构(Construction)”出来的产物。相对于前面所说的客观、统一和确定的标准单位,这样主观建构的单位也叫作意念中的单位,简称为“意念单位(Conceptual Unit)”[2],具有主观、个性和多样的特点。
意念单位作为一种思维形式,类似于认知语言学中“意象图式转换(Image Schema Transformation)”下的“一多转换(Multiplex-Mass)”,简单说就是“视多为一”或“视一为多”的思维方式和表达方式,把“很多”看作并表达为“一群”,“一群”是由很多“1个”组成,因此“一群”中的“一”,同时也有“多”的含义。如果把“一”与“多”视为对立的双方,“一多转换”表现为对立的双方的相互转化,渗透了辩证思维中对立统一的观念。
因此对于单位的认识,一方面,可以认为是约定俗成的标准单位,具有客观、统一和确定的特点。另一方面,也可以认为是主观、个性和多样的意念单位,意念单位的生成、使用和转化,就成为数学学习过程中应当逐步经历并提升的认知能力。
二、情境相同,算式多樣
对于整数乘法算式,比如“3[×]2=6”,如果其中的因数“3”表示类似于前面苹果的“3个”对象,这时“3”的意义就是“多”,表示3个“一”,这里的“一”表示的是“1个”对象。算式中另一个因数“2”,其意义是把“3个”视为“一”,表示包含2个这样的“一”,这里的“一”不再是“1个”,而是“3个”,是把“3个”这样的“多”视为“一”。
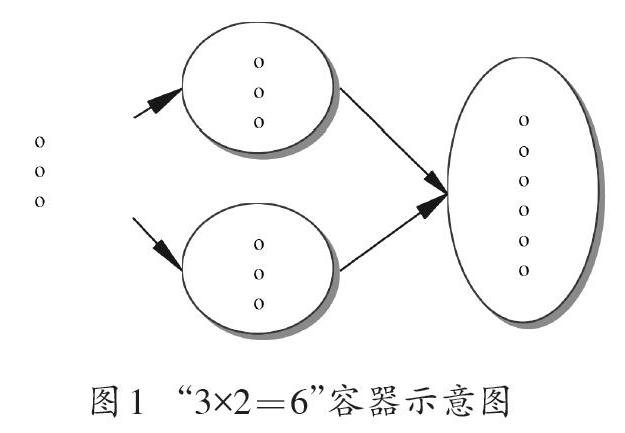
第一个因数“3”表达的是具体“对象(Object)”的属性,第二个因数“2”则不同,表达的是包含这种具体对象的“类(Collection)”或“集合(Set)”。类在认知科学中往往用熟悉的“容器(Container)”进行隐喻或类比。因此“3[×]2=6”的运算过程,可以理解为将3个对象分2次放入2个容器中,进而产生了一个包含6个对象的新容器(如图1)。
放入之前因数“3”表示“3个”对象,放入容器过程中是将“3个”对象视为“一”,结果的2类合并成为一个新的类,包含6个对象。
因此,运算“乘”在思维中具有“进入(Into)”的意义,前面提及的欧几里得《原本》中对于乘法的定义就表达了这样的意义。17世纪英国著名数学家、牛顿的老师艾萨克·保罗(Isaac Barrow:1630—1677)所著英文版《原本》第7卷的命题16这样描述乘法:“如果两个数A,B相乘,其中一个进入另外一个,产生两个数AB,BA,那么这两个数相等。”[3]这一命题实际叙述了乘法所满足的交换律,其中对乘法过程就使用了“进入(Into)”的表述。后来欧洲许多算术教科书中都沿用了这样的表述。[4]
接下来的问题是在整数乘法意义的基础上,如何认识一个分数与整数相乘?如何使得分数与整数相乘的意义与整数乘法意义进行衔接?通常的做法是利用分数加法。比如“[29×3]”,利用相同加数求和,改写为“[29+29+29]”进行计算。事实上,还可以运用意念单位的改变,认识分数乘整数。
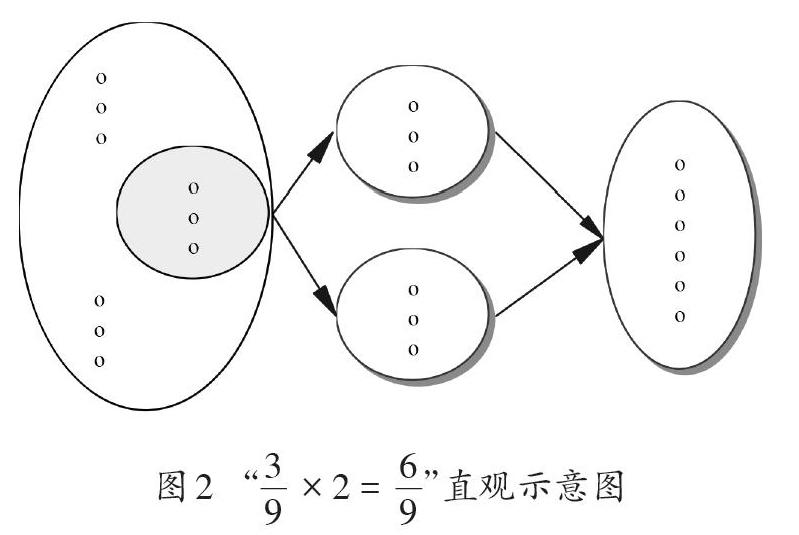
如果将算式“3[×]2=6”中因数3表示的3个对象,看作是包含于9个对象中的一个局部。把“9个”对象视为“一”,那么3个对象相对于这个“一”,就成为[39]。与图1所示整数乘法同样的过程得到的6个对象,相对于9个对象这个“一”来说,就成为[69](如图2)。
因此算式“3[×]2=6”就改变为分数乘法算式:
[39×2=3×29=69]
由此看出,两个不同的算式“3[×]2=6”与“[39×2=69]”,都表达了6个对象平均分配的过程,区别在于看待“一”的眼光不同。“3[×]2=6”是将“1个”视为“一”,“[39×2=69]”是将“9个”视为“一”。看“一”的眼光的改变,导致写出的算式不同。从两个整数的乘法,自然而然地过渡到分数乘整数。
对于除法运算也是类似,比如将6个苹果平均分给2个人,每人分3个,用整数除法算式表示为“[6÷2=3]”。如果把6个苹果看作是从9个苹果中取出来的,把“9个”看作“一”,那么6个苹果相对于这个“一”,就成为[69],分得的结果每人3个,相对于“一”,就成为[39]。相应的算式就成为:
[69÷2=6÷29=39]
因此从实际情境看,将6个苹果平均分给2个人的过程,是一个客观的事件或过程,人用数学符号表达这个事件时,就有主观、个性和多样的特点。如果把“1个苹果”视为“一”,符号表达就是“[6÷2=3]”;把“9个苹果”视为“一”,列出的算式就成为“[69÷2=39]”。因此可以知道数学认知过程的一个重要特征:情境相同,算式多样。
计算教学的一个重要内容是理解算式的意义,这样的意义一方面来源于具体的涉身活动和经验,另一方面是建立与已有知识和经验的联系。用变化的眼光看单位,可以将整数和分数视为同样对象的不同表达,分数的出现实质是人的建构,源于人看待单位眼光的改变。
前面出現的分数[39],可以约分为[13];[69]可以约分为[23]。换言之,也就是把[39]与[13]看作是相等关系,同样[69]和[23]也具有这样的相等关系。用等式表示为:
[39]=[13],[69]=[23]
如前所述,类似于此约分的过程,是看“一”的眼光发生了两次变化的结果。第一次是将“3个”视为“一”,从而“9个”就成为“3”,这个“3”表达的是3组,每一组中包含“3个”。第二次是将“3组”视为“一”,每一组就成为“[13]”,其中的“6个”就是“2组”,自然成为[23]。
因此[39]和[69]分别表达的是把“9个”视为“一”中的3个和6个,而[13]和[23]分别表达的是把“3组”看作“一”中的1组和2组。因此类似于[39]=[13]和[69]=[23]这样约分的过程,实质是在同样情境下,看“一”的眼光发生了变化,使得同样的情境出现了不同的表达。
三、方法的方法
数学教学中一个需要研究的问题是如何帮助学生原创生成解决问题的方法,也即让学生经历思考“方法的方法(Methodology)”的过程。表面看不同的算法或解题方法,实质是在同样或类似的看法和想法中生成的,这样的看法和想法是高于操作性方法的“大想法(Big Idea)”。下面以小学数学课程内容中与分数相关的问题为例加以说明。与分数相关的问题通常分为三类。
第一类:求一个数的几分之几,用乘法。
第二类:求一个数是另一个数的几分之几,用除法。
第三类:已知一个数的几分之几是多少,求这个数,用除法。
其中第三类问题也称为“知几求一”的问题,被认为是与分数相关问题中最困难的。在人教版小学数学六年级上册“分数除法”单元中的例题叙述为:
小明的体重是35kg,他的体重比爸爸的体重轻[815]。小明爸爸的体重是多少千克?
从小明体重比爸爸轻[815],可以知道小明体重相当于爸爸体重的[(1-815)=715]。也就是已知爸爸体重的[715]是35kg,求爸爸体重(知几求一)。传统的教法是让学生记住:已知一个数的几分之几是多少,要求这个数,用除法。现在是已知爸爸体重的[715]是35kg,用除法“[35÷715]”计算出爸爸体重为75kg。
像这样“模仿+记忆+练习”的学习方式,自然缺失了意义的理解。学生对于整数除法的已有经验是“等分”和“包含”,而此时所出现的算式“[35÷715]”,用等分和包含都很难解释其意义。为了规避这种困难,如今教科书中通常采用方程的方法解决问题,其算理的依据是乘除运算的互逆关系。
设爸爸体重为[x] kg,依据等量关系“爸爸体重减去小明体重比爸爸轻的部分等于小明体重”,列出方程“[(1-815)x=35]”或“[x-815x=35]”,通过解方程得到爸爸体重为75kg。这样的处理能够实现算法的合理性,但仍然缺乏对算式意义的理解。事实上,如果以变化的眼光看待“一”,可以结合学生已有经验,生成多种自然而然且合情合理的方法。
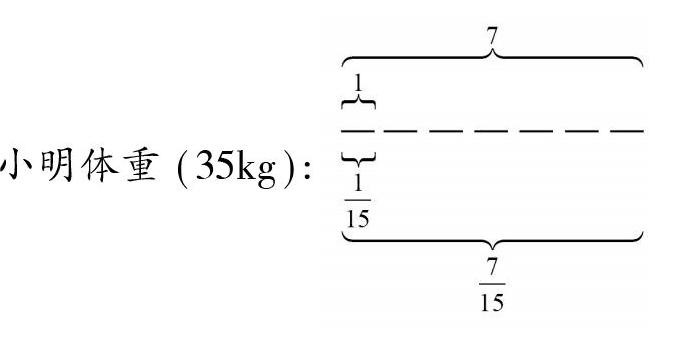
方法1:视分数单位“[115]”为“1”(如图3)。
如果视“[115]”为“1”,那么[715]就改变为“7”,小明体重比爸爸少的部分就是“8”,这样爸爸体重就成为“15”(如图4)。
问题自然而然地转化为用整数可以解决的问题:已知一个数的7倍等于35,求这个数的15倍是多少?可以用下面算式计算出结果:
[35÷7×15=75](kg)
方法2:视“小明体重”为“1”(如图5)。
如果视小明体重为“1”,那么爸爸体重就相当于将小明体重平均分为7份中的15份,用假分数表达为“[157]”,或用带分数表达为“[217]”(如图6)。
这时问题已经转变为求一个数的几倍或几分之几的指向乘法计算的问题:求35的[157]是多少?运用乘法可以计算出爸爸体重:
[35×157=75](kg)
除了上面两个方法,还可以把“爸爸和小明体重总和”看为“1”,此时相当于将“1”平均分为22份,小明体重为其中的7份,用分数表达为[722];爸爸體重为其中的15份,用分数表达为[1522](如图7)。有了这样的表达,自然建立了小明体重和爸爸体重之间的关系,学生可以在明晰关系的基础上,产生出多样的算法。
综上,看“一”的眼光是单位化的认知方式和能力,是把“一”或“单位”视为意念中的对象或实体,是主观、个性和多样的思维产物。灵活多样地选择和使用单位,可使得数量以及数量关系的表达方式随之变化。同样的对象出现不同的表达,体现了数学符号的语言特征,即表达方式的多样性。
不仅如此,看待单位眼光的改变,使得解决问题的方法呈现多样化,表面看是不同的方法,其背后具有同样的大想法。如果把解题时列出算式并且计算出结果的过程叫“做法”,那么对于单位的选择和使用,就体现了这种做法的想法,也就是方法的方法。
数学教育的初心是教育,教育的初心是人的发展。充分利用数学课程内容中所蕴含着的育人因素,使学生在数学学习过程中亲力亲为地经历认知过程、发展认知能力,实现数学的教育功能,应当成为数学教学追求的目标。
参考文献:
[1]REDMAYNE. Euclids Elements[M]. LONDON: R. Mount, F. and B. Sprint, 1714: 142.
[2]BEHR, KHOURY, HAREL, etc. Conceptual Units Analysis of Preservice Elementary School Teachers' Strategies on a Rational-Number-as-Operator Task[J]. Journal for Research in Mathematics Education , 1997, 28(1):48-69.
[3]BARROW. Euclids Elements[M]. LONDON: W. Redmayne, 1714: 153.
[4]COCKER. Cockers Arithmetick[M]. LONDON: W. Ricbardson, 1702: 38.
(首都师范大学初等教育学院 100048)

