疫情之下远程教学与辅导的案例与反思——以“独立性检验的思想初步”教学为例

华南师范大学附属中学(510630)申西芬

在疫情期间，学校以奥维亚、青鹿和智学网为课堂直播或录播播放平台的授课方式,各科组备课组也都结合学科特点,实际的教学进度,学生的学情制定出相应的教学计划安排,包括授课安排,录课方式选择,对应作业练习,答疑平台等等.本文就以选修2-3 第三章“3.2 独立性检验的基本思想及其初步应用”为例探究线上远程高中数学教学.

1 教学内容和内容解析

近几年的高考对选修2-3 第三章统计案例的要求不断提高,不仅体现在对数据计算的高要求,更重要的体现在对阅读材料中数据的提取和处理,以及真正理解题意、并能用所学工具处理实际问题的能力.在数学日常教学中,教学的重点之一就是培养学生的实践能力,所谓数学科实践能力是指学生主动参与和体验数学知识发生和发展过程,运用数学知识、思想和方法对实际问题进行分析研究,并解决问题的能力.独立性检验作为统计学中一类重要的假设检验,蕴藏着丰富的统计思想,独特的解决问题的思路,它是通过对分类变量的理解,比较两项频数,利用近似服从卡方分布的随机变量来检验两个分类变量是否有关或独立的一种常见的统计方法,具有较强的现实背景和实践意义.

2 教学目标

本节内容主要让学生理解什么是分类变量,什么是等高条形图,理解2×2 列联表的统计意义以及利用其进行独立性检验;会用χ2公式判断两个分类变量在某种可信程度上的相关性;前面学生已经学习了回归分析,知道了对于两个定量变量的相关性的判断的方法,因此本节内容也是要学生理解定量变量和分类变量的区别,即掌握独立性检验和回归分析所应用的不同背景,掌握独立性检验的一般方法和步骤.

3 教学难点

χ2的计算公式在A 版教材上没有给出推导过程,而是以构造随机变量的方式给出了计算公式.这对于有求真精神的同学来说不够,缺少了知识逻辑上的来龙去脉,或者说这个构造思想太难,无疑会挫败学生的热情.

本节有几个概念以及对χ2公式的推导过程,需要教师循循善诱,逐步启发,共同探讨,让学生体会思考的过程以及推出结果后的喜悦.但是这一点在线上教学模式下无法很好的实现.教师通常要自问自答,模拟出互动的效果其实是为了给学生思考的间隔时间.同时需要制作大量的动画来体现思考的过程和其逻辑性.

4 教学支持条件分析

疫情下,学校为教师提供了录课场所和录课技术的支持,同时也为因家庭原因不能到校录课的教师提供了录课的软件推荐,视频制作推荐教程等.本节教学内容主要采用PPT录制,小熊录屏软件录制,爱剪辑软件剪辑.作业习题以PDF格式上传至青鹿平台,作业解析通过微信发到各班级微信群,答疑辅导主要渠道是微信文字输入,微信语音输入,手写拍照,手机录制小视频,视频对话讲解过程.基本流程和方式如图-1.

图-1

5 教学内容与过程

引例为了研究物理成绩好与数学成绩好有无关系,某兴趣小组抽样调查了60 名高二学生,其中数学好的25 人,数学不好的有35 人.具体调查结果:数学好的人中有19 人物理好,6 人物理不好,数学不好的人中物理好的有17 人,物理不好的有18 人.试问:能否作出物理成绩好与数学成绩好有关的结论?

选择此题作为引例的理由:来自身边的问题,同学们有想知道结果的动力,并且和前面所讲回归分析的方法做对比,从而引出分类变量的概念.

教师(录音):有同学能给出判断吗?如果我给出这些被调查同学的数学和物理的具体成绩,你能判断吗?肯定可以的,因为我们刚学过.那大家还记得怎么做吗?(停顿思考)

教师(录音):我们可以把数学和物理的成绩用散点图表示出来,然后继续处理,这个过程用的是回归分析.那这道题我们没有具体的分数,显然不能用这个方法.因为这里的变量值也就是我们抽取的样本中的一个学生,他就只有数学好,数学不好,物理好,物理不好这样的类别属性,并不是确定的值,所以我们把这样的变量称为分类变量.而回归分析研究的则是两个定量变量即用数字来衡量的变量之间的关系.

至此完成第一个教学概念:分类变量:变量的不同“值”表示个体所属的不同类别.并同回归分析的适用条件做对比,加深学生记忆.

教师(录音):那我们应该怎么判断这两个分类变量之间的关系呢?数据在一堆文字里面看着总觉得不够清晰,怎么办呢?我们知道在处理应用题时,遇到有大量的数据,我们往往先把数据用表格表示出来.那这个表怎么列呢?我们刚才讲了,抽取的任一“变量值”的属性就是数学好,数学不好,物理好,物理不好,所以我们可以这样做:(通过动画将类别填在表中),请同学把表格完成.像如图表1 这样的样本频数列联表就成为2×2 列联表.

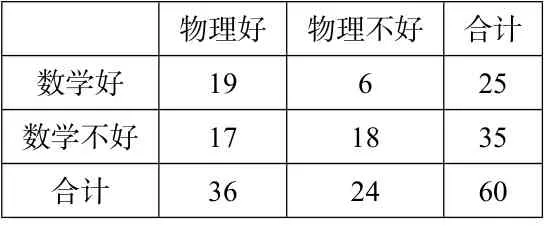
表1

如果是在课室,我们可以请同学上来画一下自己的设计表格.

在此完成第二个教学概念:2×2 列联表,即假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表即称为2×2 列联表.

教师(录音):由表格能否作出物理成绩好与数学成绩好有关的结论吗?不那么直观,我们再想办法把表格中的数据用别的方式呈现一下:我们知道在集合里面研究包含关系,我们习惯借助文氏图,这里我们也研究一下用图形表达.我们先做出两个矩形,分别代表数学好和数学不好,然后在矩形里面分别选一部分表示物理好,这样可能就比较直观了.为了更好的对比,我们将两个矩形应该怎么样处理呢?一样高还是不一样呢?(停顿思考),为了更好的对比,肯定是一样的,那最简单我们用1 来表示,然后物理好的部分都靠同一侧,用比例表示,这样就很直观了.如图2,这样就能将本题直观的表现出来了,这个图叫做等高条形图,这种比较分类变量是否有关的方法叫做等高条形图法.比较图中两个深色条的高可以发现,在数学好的样本里物理好的频率要高些,因此直观上可以认为数学成绩好更容易物理成绩好.

图-2

至此我们完成第三个教学概念:等高条形图法;特点:计算量小,直观.

教师(录音):还有别的方法吗?(停顿思考)

此处启发学生思考,回顾判断两个变量相关的方法.

教师(录音):我想已经有同学想到了,我们之前学过判断相关或者无关(独立)的方法.对,就是概率方法.我们可以尝试去推理.为了具有一般性,我们用字母来代替表1 中的事件和数据,得到表2:设数学好为事件A,物理好为事件B,则数学不好为事件,物理好为事件.那请大家思考:事件A与B有关,无关什么意思呢?(停顿)我们知道:事件A与B无关等价于:P(AB)=P(A)P(B)成立.我们不妨做个假设,记作H0:物理好跟数学好无关,并称之为统计假设,则在此假设下必有:.

表2

比较小,而这个式子就是统计学中非常有用的卡方统计量.

统计学之父英国数学家皮尔逊推导得出:实际观察次数f0与理论次数fe之差的平方再除以理论次数fe所的统计量,近似服从卡方分布,可表示为:,而(*)式化简得:.

这个就是随机变量K2读作卡方,在计算中,也会记成k(卡方的观测值).

至此,我们推导出了本节难点之一卡方公式的计算公式.此时可能部分学生有点懵,不知道什么意思或者怎么用,接下来需要解释.

教师(录音):刚才的推导过程其实就是一种反证法的过程.我们假设事件A 与B 无关,近似等价成K2接近于0,所以若计算得出的K2值越小,那说明越有把握认为假设是正确的;反之若K2值较大,则可以拒绝假设,即承认事件A 与B 有关;也可以用小概率原理来解释.小概率原理就是概率很小的随机事件在一次试验中一般不会发生.首先假定假设正确,从总体中抽取一组样本进行检验,在假设成立的条件下,如果样本观察值导致了“小概率事件发生”,这与“小概率原理”矛盾,就应该拒绝假设,否则则接受假设.具体参照值查看卡方分布概率分布表,表3.

表3

表中k0,就是卡方计算值的临界值,也就是在某一可信度下判定分类变量无关的下界.

比如:当K2≥3.841 时,就说有95%的把握说事件A与B 有关[1];当K2≥6.635 时,就说有99%的把握说事件A与B 有关.

这里说明几点:在B 版教材中明确指出一般都以这两个临界值来判断,并且指出当K2＜3.841 时,认为事件A 与B是无关的[2].但是A 版教材中没有明确给出,事件A 与B 是无关的临界值.但是在高考题中一般是很明确的指出.所以同学们无需担心.像这样利用随机变量K2来判断“两个分类变量有关系”的方法,称为独立性检验.

至此,我们推导出了本节最后一个概念:独立性检验.学生可能会跃跃欲试.下面小试牛刀.

教师(录音):下面就用引例计算一下.请同学们按下暂停键:由K2计算公式得:4.57,∵4.57＞3.841,∴我们有95%的把握认为数学好与物理好有关.

教师(录音):做几点说明:①对于引例,最理想的解决办法是调查所有相关的人,然后对得到的数据进行统计处理,但这花费的代价太大,实际上是行不通的.②60 个人相对于全体,只是一个小部分;③现在我们用部分对全体作推断,推断可能正确,也可能错误.④计算时可以用K2表示,也可以用k.下面做练习.

练习主要是让同学们更加熟悉卡方公式及其统计意义.

教师(录音):接下来我们还有两道例题:请同学们按下暂停键先读题:

例1巴西医生马廷恩收集犯有各种贪污、受贿罪的官员与廉洁官员寿命的调查资料:500 名贪官中有348 人的寿命小于平均寿命,152 人的寿命大于或等于平均寿命;590 名廉洁官员中有93 人的寿命小于平均寿命,497 人的寿命大于或等于平均寿命.这里,平均寿命是指“当地人均寿命”.能否在犯错误的概率不超过0.01 的前提下认为官员在经济上是否清廉与他们寿命的长短之间有关系?

解据题意列2×2 列联表如下表4:

表4

假设官员是否清廉与它们的寿命长短无关.

由K2公式得:325.635,因为325.635＞6.635,因此,在犯错误的概率不超过0.01 的前提下认为官员在经济上是否清廉与他们寿命的长短之间是有关.

本题的设计意图在于让同学们自己建立2×2 列联表同时熟悉另一个临界值,进一步熟悉解答题的书写格式,同时注意到题目的询问方式是与前面不同的,给出了判断的标准.

例2为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查的结果列在表中,根据所选择的193 个病人的数据,能否作出药的效果和给药方式有关的结论?

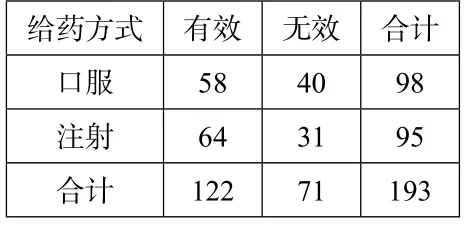
表5

解 设H0:药的效果与给药方式没有关系:由K2公式得:因为1.3896＜3.841,因此我们没有理由说“药的效果”与“给药方式”有关,可以认为“药的效果”与“给药方式”无关.

本题主要说明的点是当算出的卡方值小于3.841 的时候,我们往往判定没有关系.我们在查临界值表前,是有个标准的,一般是奔着两个临界值3.841,6.635,教材和高考题基本也都是,我们要与教材和高考保持一致!如果在题目中有具体的问法,则可以尊重题目,比如问有没有97.5%的把握,那我们要找对应临界值:5.024.

教师(录音):小结:①我们有95%的把握说事件A 与B有关,是指推断犯错误的可能性为5%,这也就是常常说成是“以95%的概率”,其含义是一样的;②统计的基本思维模式是归纳的,它的特征之一是通过部分数据来推测全体数据的性质,因此,统计推断是可能犯错误的;③我们从数据上体现的只是统计上的关系,而不是因果关系;④使用卡方统计量作2×2 列联表的独立性检验时,要求表中的4 个数据都要大于5,为此,在选取样本的容量时一定要注意这一点.

6 教学效果

根据收集同学们的反馈,对于线上教学(本节为例)按照优缺两个方面汇总如下:

优点:①线上教学可以调进度,可以在听不懂的地方回放,比如这节课公式的推导过程;②线上上课可以更清楚的看到过程,不用担心老师擦掉(黑板),可以更好的记录要点和笔记,可以下载保存;③不用担心自己不知道,其他同学知道了而焦虑;也避免出现因为很多同学都懂了老师不讲了的尴尬!④一部分学生很享受这种学习方式,可以避免同学的干扰,自己独立思考的时间更多!

缺点:①不能和老师同学互动,偶尔会觉得枯燥;②没有机会听到其他同学分享的好想法;③心态会相对放松,因为没有老师突如其来的提问,少了些专注力和紧张感;④遇到问题不能及时发问,不能及时得到老师和同学的指点;⑤长期对着电子屏很伤眼睛!

教师方面反馈:根据每次的练习提交情况,发现95%以上的学生都能按时提交作业,并且正确率比较高;但是可能存在假学现象,另外,问问题的频率,比在学校有所减少.测试没有办法严格控制时间,有学生会不按照规定时间提交!

根据家长的反馈,存在个别学生在家沉迷游戏,懒散不自觉,会有应付作业等情况,没有在学校学习高效认真!

综上所述,疫情阶段极有可能是学生成绩两极分化的发展阶段;复课后一定要及时处理这个问题,必要时要开设扶弱课程,因为对于高二学生来说,开学已近高三.此外复课后会对学生做个测试,请同学们用独立性检验判断教学方式(线上、线下)和学习成绩有无关系.