谈“三角函数的概念”教学——比较新旧人教版教科书中“三角函数的概念”的引入方法

广东省深圳市龙岗区横岗高级中学(518115)梅锋

近来,根据《普通高中数学课程标准(2017年)版》编写的新人教版《普通高中教科书·数学》在包括广东省在内的全国多省市推广使用.新的教科书,无论从知识体系的编排,还是具体到个别概念的引入,都与之前的教科书有了很大的变化.

如何体现新课程标准的理念,在实际教学中提高学生的数学素养,是我们每一节课上课前都必须深入思考的问题.手握着新的教科书,我们该如何科学使用它来为我们的教学服务,面对着刚刚入学的高一新生,我们该如何引导他们在已有的学习经验的基础上进一步学习和研究数学,对我们来说是一个全新的课题.

在数学教学中,每一个新概念的引入,都是继续学习相关知识的基础.所以,概念教学就显得尤为重要[1].有些数学概念,如果引入的方法不恰当,学生理解和掌握起来非常困难,就会对后续知识的学习造成无可挽回的损失.这就要求我们在教学中要慎重对待每一个基本概念的引入和讲授,要以学生为本,从学生的实际出发,在学生已有的知识架构上进行建构,用符合他们的认知规律的方法来进行教学.

以三角函数的概念为例,三角函数的定义是后续学习三角函数相关知识的基础,但三角函数的定义却不容易被学生理解和掌握.如何让他们在初中已经学过锐角三角函数的基础上以全新视角来理解任意角的三角函数,需要有一个合适的思维衔接.在这部分知识的处理上,新旧两版教科书体现了各自不同的特点.旧版突出了旧知识往新知识的过渡[2],由初中的锐角三角函数是“比值”上升到任意角的三角函数是单位圆上“点的坐标”,再分析三角函数的函数本质;新版体现了知识的探究和生成过程[3],先着重强调函数的本质是一种“对应关系”,再给出三角函数的定义.

比较新旧两版人教版教科书,在三角函数的概念的呈现上,各有千秋.

1 旧版编排内容及特色

以问题出发,引导学生复习回顾初中所学的锐角三角函数的定义,以此为基础来探究直角坐标系中角的终边上的点的坐标与锐角三角函数的关系,任务指向非常明确,操作流程清楚,学生根据已有知识来探究非常容易上手,运用数形结合法,根据图形容易推理出相关结论.

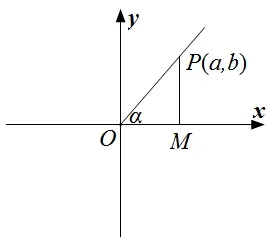
图1

接着进一步根据学生已有的相似三角形的知识,使学生明白角的终边上的点(除顶点外)无论位置如何变化,三个三角函数的值都不会改变.运用从一般到特殊的方法,引出单位圆概念,进而实现在单位圆上定义三角函数的目的.

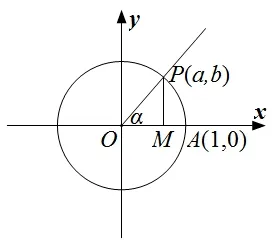
图2

至此,已经让学生知道,除了之前所学的直角三角形定义法,锐角三角函数还可以用角的终边在单位圆上的点的坐标来定义,为任意角的三角函数的定义的提出打下思想基础,接下来给出任意角的三角函数的定义就顺理成章了.

最后,在给出任意角三角函数的定义之后,回扣“函数”的概念,明确了三角函数定义与三角函数概念之间的关系,消除学生容易产生的误解.指出三角函数的本质是角的集合与实数集之间的一一对应关系,三角函数就是角的函数,三角函数的值并不是由终边上点的坐标来决定,而是由角的大小来决定,只是为了方便,我们借由角终边上的点的坐标来表示三角函数的值.

笔者认为,这样的编排方法,至少有以下几个优点:(1)图文并茂,形象直观,易于学生理解和掌握;(2)温故知新,衔接紧密,从学生实际出发;(3)精巧设问,循循善诱,注重数学研究方法的渗透;(4)过渡自然,环环紧扣,体现了数学逻辑的严密性.

2 新旧版教科书编排方式对比

我们通过下表对新旧版教科书的三角函数内容进行比较.

旧版新版内容呈现方式特点呈现方式特点导入问题导入:你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗?从已有的知识出发问题导入:如何建立数学模型,刻画单位圆上的点P 的位置变化?单刀直入,引导探究知识探究锐角三角函数的比值定义→坐标定义;角终边上任意的点→单位圆上的点;锐角→任意角.体现从特殊到一般和从一般到特殊的思想,无具体实例,高度抽象设计三个特殊的角,让学生探究,发现角能唯一确定它的终边与单位圆的交点的坐标,体现函数思想.探究实例,形象具体定义提出先给出正弦、余弦、正切等名称,回避函数概念.形式统一,避开模糊地带直接给出正弦函数、余弦函数的定义;对于正切先给名称,以示与正切函数定义区分.考虑细致,用语精确,注意细微差别定义解读考虑终边的特殊位置,对正切做特别说明.思维严谨,关注特殊考虑终边的特殊位置,对正切做特别说明,再提出正切函数的定义.关注特殊,消除思维误区形成概念揭示本质:正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.从定义到概念,从内涵到外延在前述的基础上直接给出三角函数概念;通过设置探究问题,将锐角三角函数与任意角的三角函数统一起来.顺理成章,水到渠成例题设置例1 直接运用定义求解;例2 先要运用转化思想,再用定义求解.且在例2 后设置思考题,引导学生探究已知角终边上任意一点的坐标,如何求三角函数值.由易到难,阶梯上升,拓展课外例1 直接运用定义求解;例2 先给出结论,要求学生证明已知角终边上任意一点的坐标,可得三角函数值的比值公式.具体到抽象,重要结论问题化习题设置3 道习题,其一考查用定义法求三角函数的值,其一考查用比值法求三角函数的值,其一要求学生计算并记忆特殊角的三角函数的值巩固知识,考查全面4 道习题,前3 题与旧版基本相同,增加一道应用题,考查学生运用三角函数模型解决实际问题的能力巩固知识,强调应用

3 新版编排内容及特色

同样是从问题出发,对于本章前言部分里所提出的如何刻画做圆周运动的点P的位置变化的问题,运用从特殊到一般的思想,直接提出先研究单位圆上点的运动.

接着引导学生利用直角坐标系来研究以原点为圆心的单位圆上点P的坐标与它对应的角α之间的关系.为了便于学生研究,设置了探究环节,明确提出了探究的目的,让学生初步感受角α可以唯一确定点P的坐标,逐步形成函数概念.在设置探究项目时,特别选取了来让学生探究,这几个角各具代表性,又是常见的和和学生熟悉的,容易上手,再次体现了从特殊到一般的思想.由给定的特殊角来确定点P的坐标,书中给出了具体的方法为运用勾股定理,有了方法指导,学生探究起来就可以得心应手,这样设置贴合学生的实际,降低了探究的起点,容易激发学生的学习热情.

对特殊角进行研究,揭示了角α的终边与单位圆交点P的坐标与角α之间的对应关系之后,三角函数的概念就呼之欲出了,接下来给出三角函数的定义就水到渠成,然后书中直接给出了三角函数的定义.但是在定义正切函数时,为了突出点P的纵坐标与横坐标之比即时无意义,先行给出了“正切”的定义,仔细分析之后再给出正切函数的定义.

在给出三角函数的定义之后,又一次设置探究环节.通过探究,使学生明确虽然定义方法不同,初中所学的锐角三角函数的定义与现在给出的任意角的三角函数的定义是统一的.这里体现了从一般到特殊的思想,体现了数学定义的有机统一性.

最后,在例题的设置上,特别注意到用问题来说明,三角函数除了利用单位圆上的点P的坐标来定义,还可以用角α的终边上的任意一点(除原点外)P的坐标来定义.消除了学生的思维误区,扩展了求任意角的三角函数值的思维,这里运用了从特殊到一般的思想.

新版的布局,也体现了独有的特色,优点也不少:1.前后呼应,解除疑惑,从学生近期学习的内容和遇到的问题出发;2.突出探究,鼓励动手,让学生在探究中发现规律,体会数学研究的乐趣;3.特殊出发,回归一般,注重基本数学思想的渗透;4.精心设题,拓展思维,让学生体会做题后反思提升的必要.

4 教科书使用方法探索

笔者曾尝试分别严格运用新旧两版教科书的编排顺序来推进课堂教学.

相较之下,用旧版来教学,教学进程推进更加顺利.学生从锐角三角函数的直角三角形定义出发,过渡到锐角三角形的角终边上点的坐标定义,再到单位圆的引入,再到任意角的三角函数的定义的给出,层层推进,思维顺畅.但学生能自主探究的部分不多,需要老师不断引导.学生缺少了参与知识的生成过程,缺乏体验感和成功的喜悦,课堂总体比较沉闷.

用新版来教学,教学进程推进会时而受阻.课开始不久,就迅速进入了探索环节,在引导学生运用勾股定理求三种情况下点P的坐标时,不少学生遇到了困难,很多同学不记得有一个角是的直角三角形的三边之间的长度关系.最快求出坐标的同学,基本上都是运用了初中学过的锐角的三角函数的定义.随后直接给出了任意角的三角函数的定义,有些突兀,感觉过渡不自然.而后面的探究锐角三角函数的定义与任意角的三角函数的定义的关系,因为没有具体给出探究方法,起初学生不知所云,无从下手,而后当学生知道了运用构造直角三角形来验证后,又感觉有些多余,学生基本上无事可干.此外,笔者觉得例2 需要证明的三个结论,让学生自主证明有些勉为其难.这三个结论是该作为任意角三角函数的定义的延伸,从单位圆上的点扩展到终边上任意一点(除原点外)来讲解,还是作为例题来供学生研究,值得商榷.虽然课堂推进遇到了一些困难,但学生参与探究的热情空前高涨,不少探究成功的学生所体现出的自豪感无以言表,这说明我们在课堂上要给学生更多展示自我的机会.

5 反思和改进建议

我们要把新旧两版教科书的优点结合起来,更好地进行课堂教学.既要兼顾知识的连贯性,也要兼顾学生的参与率,除了不为本是从,照本宣科,要灵活运用教科书,还要从学生实际出发,精心设计教学的每一个环节.

根据建构主义学习理论,本节内容的编排,应该继续坚持从学生已有的知识和经验出发.例如旧版从锐角三角函数的定义入手,更加贴合学生的实际,逐层推进,从特殊到一般,符合学生认识规律.要合理设置一些探究项目,使学生参与到知识的生成过程中来.在设置探究项目时,目的要明确,方法要具体,操作性要强.例如新版设置了探究单位圆上点的坐标与点所在终边的角的关系,探究目的和方法都非常明确.

对于教科书的使用者,我们不要拘泥于书的内容来推进教学,可以适当调整教学内容和顺序,甚至增繁就简.对于教科书的编者,本节内容的编排,笔者有一些不成熟的见解,基于旧版,进行一些微调,或许更加有利于教学:

首先，在给出单位圆的定义之后,任意角的三角函数定义之前,设置探究项目.探究1:用锐角三角函数的知识,求出和的三个三角函数的值,看它们与角终边上且在单位圆上的点P的坐标有何关系?求出和的终边上且在单位圆上的点P的坐标,你能类似地得出几组等量关系吗?

其次，在任意角的三角函数定义之后,设置探究项目.探究2:在的终边上取一点P,使得OP=2,运用锐角三角函数的知识,求出P点的坐标,横、纵坐标分别除以2后的值与的三角函数的值有何关系?在的终边上取一点P,使得OP=r,运用锐角三角函数的知识,用含r的式子表示P点的坐标,横、纵坐标分别除以r后的值与的三角函数的值有何关系?

在探究2 之后,给出结论:三角函数的值不会随着点P的位置的改变而改变,三角函数的值由角的大小来决定,所以三角函数是角的函数.只要知道角α终边上任意一点P的坐标(x,y),就可以求出角α的三个三角函数的值.

为了更好体现三角函数与单位圆上P点横、纵坐标的对应关系,将书中出现的三种三角函数的顺序调整为先余弦,后正弦,再正切.