“胡不归”问题的求解策略
2021-08-05 06:49苏国东
数理化解题研究 2021年17期
苏国东
(广东省广州市真光中学 510380)
近年来各地中考多次出现以著名的“胡不归”问题为背景命制的压轴题,着重考查了学生的几何直观能力和动态思维品质.
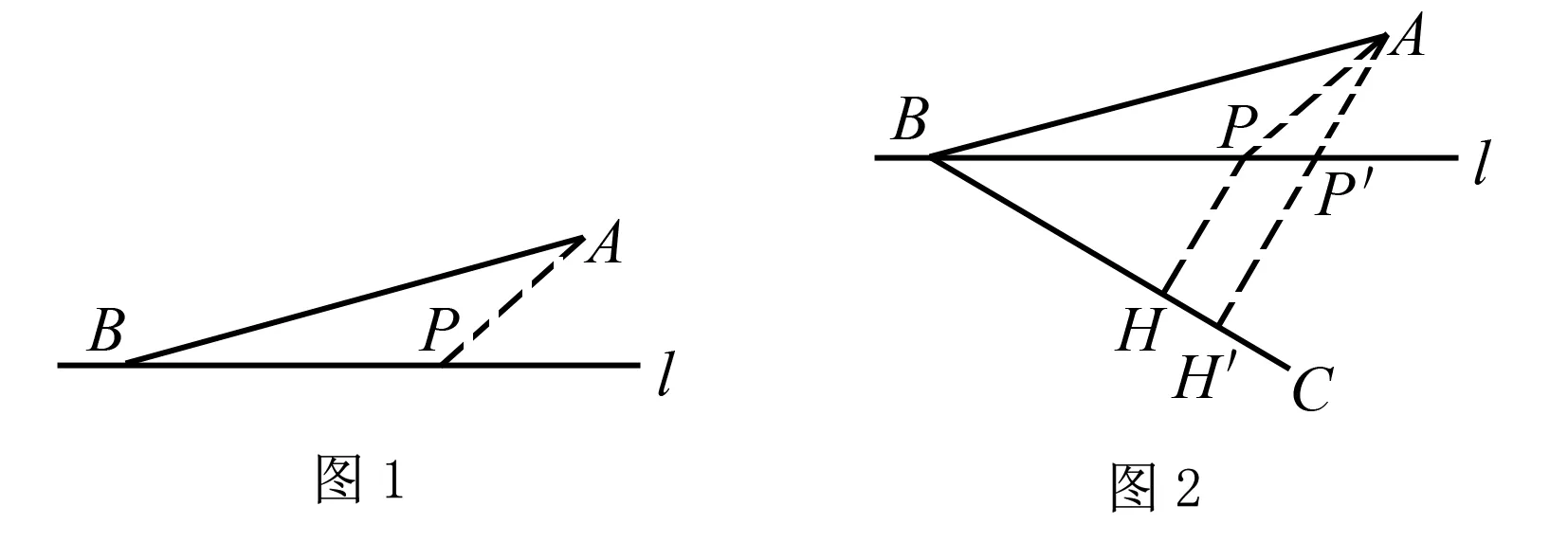
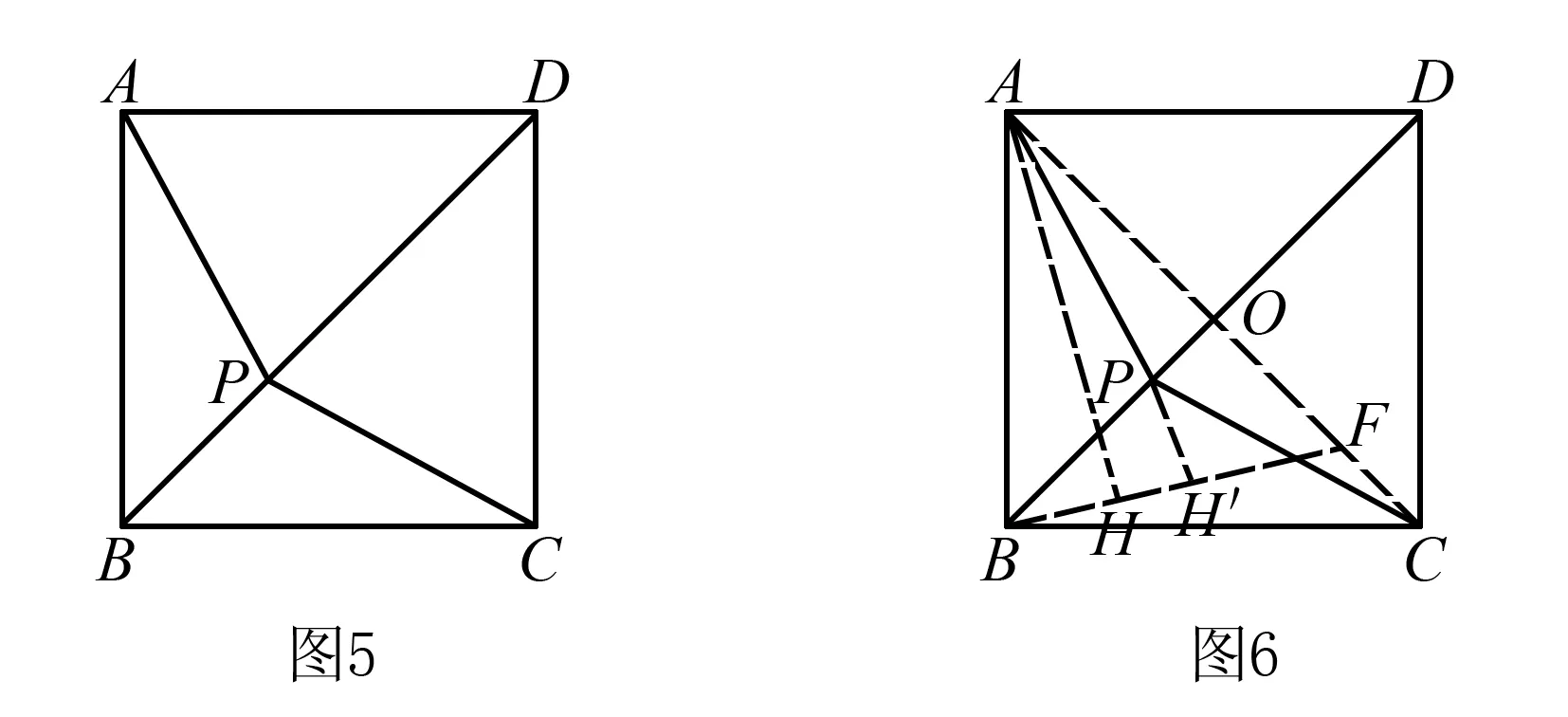
“胡不归”问题,指的是形如PA+kPB型的最值问题,其中0 本文通过引例归纳出“胡不归”问题的求解策略,并结合三个具体案例进行阐述. 由此归纳出“胡不归”问题的求题策略如下. 第一步:以PB为一边作一个角(角的另一边和PA位于PB的两侧),使其正弦值等于k. 第二步:过动点P向角的另一边作垂线段PH,构造直角三角形PBH,则有PH=kPB,将问题转化为求PA+PH的最值问题. 第三步:利用垂线段最短,当A、P、H三点共线时PA+PH取得最小值. 例2 (2018年连云港中考模拟):如图5,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( ). (1)略; 此时xE′=xD=2,yE′=DC=3-2=1,所以点E′的坐标为(2,1),点M在整个运动中用时最少.一、问题求解策略



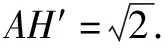
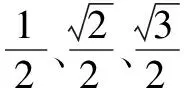
二、案例分析



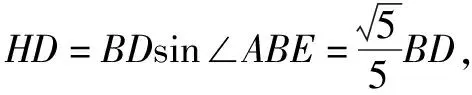
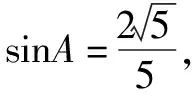
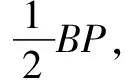
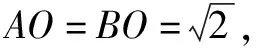


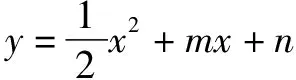


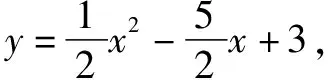
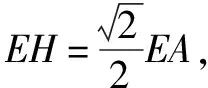
猜你喜欢
新世纪智能(教师)(2021年2期)2021-11-05
小学生学习指导(中年级)(2021年10期)2021-11-01
中学生数理化·中考版(2021年8期)2021-07-31
海洋通报(2021年2期)2021-07-22
学生天地(2020年19期)2020-06-01
中学生数理化·七年级数学人教版(2019年10期)2019-11-25
求知导刊(2017年30期)2018-01-17
广东教育·高中(2017年7期)2017-09-01
福建中学数学(2016年2期)2016-10-19

