综合法和解析法在初中几何解题中的应用探讨

杨静静

(江苏省苏州工业园区娄葑学校 215100)

随着课程改革的不断推进与发展，初中数学教学中实施有效教学已成为教师追求的目标，也是培养学生的数学核心素养的重要方面.目前，就初中几何教学来说，大部分学生对几何学习达到困难，有些学生即使对相关的几何概念能够掌握，也无法在解题过程中做到灵活运用.因此，教学中教师积极采用综合法和解析法，引导学生在解题中解决几何问题，能够取得事半功倍的教学效果.

一、综合法和解析法概念

综合法是一种对图形直观分析和逻辑论证相结合的方法，是在解决几何问题过程中最基础的一种方法，可以有效培养学生的逻辑思维能力.通过让学生更直观的了解几何图形，然后将题目中的条件联系起来，最后得到结果.解析法与综合法的区别在于其从问题出发，属于一种逆向思维.先了解要得到的结论，然后寻找充分必要条件最终解决问题.在解题过程中，学生一定要灵活运用这两种数学方法解决几何问题，综合法和解析法并不是单独存在的，两者可以相互渗透、相互转化，形成综合—解析法，更好的解答几何问题.

二、初中几何解题过程中遇到的问题

学生是教育教学的主体，随着新课改的深入推进，这一理念已经受到了广大教育工作者的认可.但是在实际教学过程中，为了更好的把控课堂，部分教师依旧会主导课堂走向.如果教师经验不足，很容易占用大部分的课堂时间，这样留给学生的时间相对较少，学生无法吸收和消化课堂教学内容，在今后解题过程中会遇到较多问题.而几何习题需要学生有自己的理解并建立相关思维，教师主导课堂会影响学生自主思考能力的发展.在遇到简单的问题时，学生可以凭借自己的能力去解答问题.但是当问题较难时，学生就会向依靠教师解决问题，长此以往，学生对教师的思维依赖越来越严重，逻辑思维及创新思维难以得到发展.此外，教师只注重把控课堂秩序，而忽略学生学习习惯的培养，也不利于学生学习能力的发展.

对初中学生来讲，几何习题有着较大的难度.如果直接开始课堂教学，学生很难吸收全部知识.这就要求学生要在课前进行相关知识的预习，这样才能跟上老师的节奏.随后在课堂完成后进行相关知识的总结，从而将知识内容内化，构建自身的知识体系，确保更好的解决相关问题.但是由于教师忽略对学生学习习惯的培养，学生不注重课前预习与课后复习的重要性，因此在知识掌握方面存在不足，在今后的解题过程中也容易出现各种各样的问题.

三、如何让学生更好的掌握数学思想和方法

对于初中数学几何教学，教师一定要给予充分的重视，作为教学过程中的重点，几何问题在考试中会占有较大的比重.同时由于其对学生的几何思维能力有着一定的要求，所以属于教学过程中的难点.如果不能吸引学生的学习兴趣，让学生更好的理解知识，很容易遇到相同题型，却不会解的现象.

首先，教师要尊重学生的教育主体地位，这不仅是在意识中，更应体现在实际的课堂教学中.给予学生更多的思考时间可以让学生消化教师讲解的知识，还有助于培养学生的自主思考能力和创新思维.

其次，教师要帮助学生养成良好的学习习惯.在课堂开始前，教师要引导学生先进行课堂知识预习.预习让学生大致了解课堂内容，并且发现教学内容的难点所在，然后带着问题去听讲，从而提升学习效率.所以教师要鼓励学生主动进行课前预习，然后老师可以在课堂中专注于重难点问题，在有限的课堂时间内帮助学生更好的理解知识，提升教学质量.教师还应当提升课堂趣味性.因此在课堂教学中，教师应当多引入一些学生感兴趣的内容，让学生更好的投入到课堂中，改善课堂气氛.在这样的氛围下，学生也更愿意与教师主动交流.教师也能在交流过程中了解到学生的学习问题所在，然后改进教学策略和计划，帮助学生更好的进行课堂学习.在课堂学习后应及时复习，可以让学生解决课堂学习中的疑惑，提升学习效果.教师也可以为学生构建学习体系，在学生经过一段时间的学习后，采用合适的方法进行复习，然后了解自身学习体系存在的不足并加以完善，完成思维拓展.因此，在教学中学生会更好的掌握几何思想和方法，提升知识掌握程度，从而更灵活的解决相关问题.

四、运用综合法和解析法解决初中几何习题的实例

1.综合法

如图1，AB∥CD，直线EF与AB，CD分别交于M，N，MP平分∠AMN并交CD于点P，MQ平分∠BMN并交CD于点Q.求证:PN=QN.

图1

解因为AB∥CD，所以∠AMP=∠MPN，∠BMQ=∠MQN

因为MP平分∠AMN，所以∠AMP=∠PMN

因为MQ平分∠BMN，所以∠BMQ=∠QMN

所以∠PMN=∠MPN，∠QMN=∠MQN

所以PN=MN，MN=QN，所以PN=QN.

2.解析法

如图2，在平行四边形ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F，求证:AE=CF.

图2

解析法要采用逆推的思想，所以要从结论出发，最终解决问题.

解要证明AE=CF，需要求证三角形ACD与三角形CFB全等.由角边角定理可知，两个角和一条边对应相等，则可以说明两个三角形全等.

所以只用求证两个三角形的对应角相等，同时有一条相同的边就可以求解.

因为四边形ABCD是平行四边形，所以AD=BC，并且∠A=∠C

已知条件中DE⊥AB，BF⊥CD，所以∠AED=∠CFB，符合条件.

所以采用解析法可以证明AE=CF.

3.解析—综合法

如图3，平行四边形ABCD的对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点.求证:四边形EFGH是平行四边形.

图3

解首先采用解析法分析问题，想要证明四边形EFGH是平行四边形，就需要求证EO=GO，且FO=HO.

然后采用综合法，根据已知条件，求证想要得到的结论.

因为四边形ABCD是平行四边形，所以AO=CO，BO=DO.

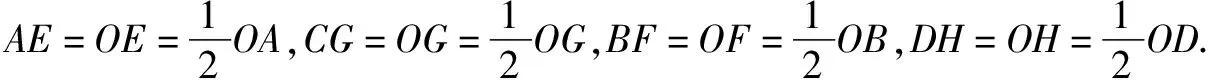
所以EO=GO，FO=HO，所以四边形EFGH是平行四边形.

总之，综合法和及解析法作为重要的几何思想，学生一定要掌握这两种方法的含义.在解题过程中，学生要根据具体问题具体分析，采用合适的解题方法，高效率的完成习题解答，在保障速度的同时提升准确率.