借助逆向思维 解答数学难题

郎烈骏

(安徽省庐江第四中学 231500)

逆向思维又称求异思维，是对似乎已成定论或司空见惯的观点或事物从相反视角思考的一种思维方式，从思维的对立面方向思考和探索，继而创立新形象和形成新思想.在初中数学解题训练中，当出现难题时，采用常规方法无法处理时，教师可提示学生基于逆向视角切入，重新审视题目内容，使其极力发挥个人思维优势，最终辅助他们顺利解答数学难题.

一、打破题目固有顺序，借助逆向思维解题

针对初中数学解题教学来说，学生的思考与处理通常会受到固定思维的影响，喜欢按照一样的步骤完成解答，由于通过多次重复性联系，他们的个人思维模式慢慢成型，难以转换过来.初中生采用这样方法处理简易题目时可能非常有用，当遇到难题时就极易陷入到困境当中，无法准确找到突破口，这时数学教师可引导学生打破题目的固有顺序，把题设内容颠倒过来，使其借助逆向思维来解题，从而提升他们解题的实际效果，有效处理数学难题.

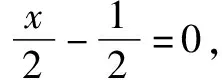
二、借助逆向思维优势，反面思考解答难题

逆向思维是相对于正向思维而言的，在日常生活中，人们通常习惯于沿着事物发展的正方向思考问题且寻求解决办法，当遇到障碍时，可从反面视角出发，倒过来思考，从求解回到已知条件，反过去想或许能让问题变得简单化.在初中数学解题教学中，对于难题的解题而言，当从正向视角思考很难解决时，教师就可鼓励学生借助逆向思维优势，尝试进行反面思考，重新整理题干信息，把难题变得简便且易于处理，帮助他们正确求出难题的答案.

例2当取什么实数时，抛物线y=-x2+(m-2)x+m-5的顶点不在第四象限？

分析当抛物线的顶点“不在第四象限”时，所指的范围相当广泛，不仅其它三个象限均可，还可以在横纵向轴上面，假如学生对这几种情况进行逐个讨论，结合各种情况下的结果求出m的集合，再确定共同的部分，这样讨论范围比较大，他们很难精准无误的计算.所以说教师可以指导学生借助逆向思维优势反面思考这一试题，直接求出抛物线的顶点在第四象限时实数m的集合，再剔除这部分，就是题目答案，显得较为简便.

三、运用反证逆向思维，顺利处理数学难题

反证法属于间接证明方法中的一种，当处理某些难题用直接证法比较困难时，往往使用反证法.在初中数学解题训练中，针对不少难题的解答，教师可指引学生运用反证法处理题目内容，即为对逆向思维的应用，使其从结论的反面展开思考、分析、交流与探讨，由此降低题目的难度，让他们在训练过程中慢慢形成逆向思维，能够准确处理数学难题.

例3如图1所示，已知点D与点E分别是AB与AC上面的点，BE与CD交于O点，假如OB=OC，AD=AE，尝试说明OD=OE.

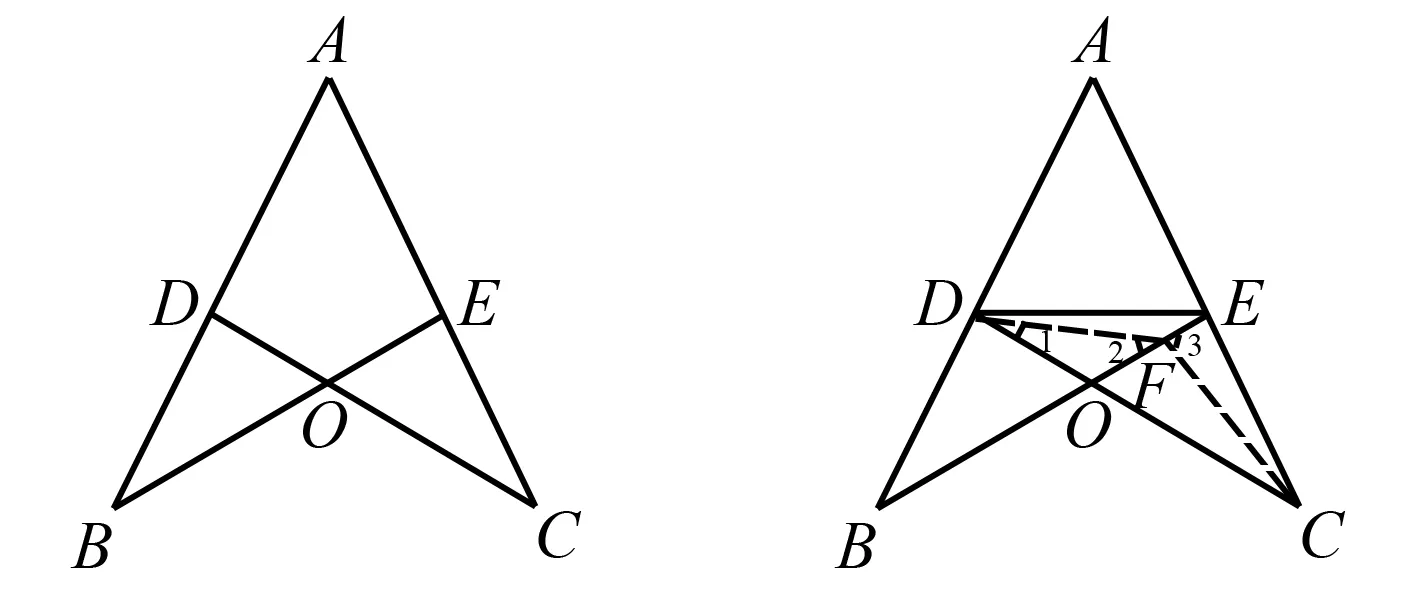
图1 图2

分析处理本题时如果学生基于正面视角出发，需要考虑的方面较多，难度较大，要先画一个辅助圆，经过A、B、C三点，再结合全等三角形的相关性质说明.教师可提示学生借助逆向思维依靠反证法尝试说明，假如OD与OE不相等，当OD∠3，从中推断出∠BDO>∠3，依据∠EDO>∠1，∠1=∠2，∠2<∠DEO得出∠EDO>∠DEO，说明∠BDO+∠EDO>∠3+∠DEO，则∠BDE>∠CED.另外，∠BDE与∠ADE、∠CDE与∠AED均是互补关系，说明∠ADE<∠AED，AEOE时，运用同样的方法说明AD>AE，也与题设条件不符，故说明OD=OE.

四、基于结论视角切入，借助逆向思维证明

初中数学解题训练主要分为代数与几何两大部分，几何证明类问题作为一种比较常见的题型，同样存在着不少难题，不过无论题目难易程度如何，往往需要从两个方面切入.一方面是利用题目中给出的已知条件，通过正向推理以后就能够轻松得出结论.另一方面是从待证的结论着手，思索为证明结论所需的具体条件，及现存与缺失条件，假如发现条件不足的话，教师引导学生基于结论切入，使其借助逆向思维证明，让他们推理出结论与条件的契合.

例4如图3所示，已知在△ABC中，D与E都是AC边上的点，且AB=AD，BD是∠CBE的角平分线，请证明AD2=AE·AC.

图3

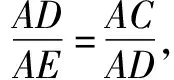
在初中数学解题训练活动中，教师应保证学生具备扎实而丰富的“双基”知识为前提，有意引领他们借助逆向思维优势处理与解答数学难题，这对克服思维呆板与思维定势来说有着积极意义，使其摆脱固有思维的限制与束缚，思维变得更为灵活，最终突破难题障碍.