《线性代数》中的形似化教学探索

杨 扬， 张 萌

(1.西北工业大学 航空学院，西安710072； 2.长安大学 理学院，西安710064)

1 引 言

《线性代数》是高等院校理工科各类专业的公共必修课程之一，其中涉及逆矩阵、最大线性无关组、特征值与特征向量、方阵的相似对角化等众多重要但抽象的概念.教学中发现：关于上述概念的典型例题，大部分学生在求解时大方向是可以把握的.而一旦题目巧妙变动，错误率便会明显升高，甚至有些学生毫无思路，无从下手.之所以出现这种情况，其关键在于学生对基本概念的理解不够透彻，在相关概念的辨析和逻辑关系梳理上存在漏洞.为了便于学生理解，许多学者在概念的讲解上进行了大量有益的探索，如从线性变换的角度引入特征值与特征向量的概念[1-2]，通过概念类比和内容重构的方法讲解线性代数中向量组的线性相关性、克拉姆法则、线性空间等知识点[3-6]，通过案例化教学穿插引入方阵的相似对角化知识[7-8]等.这些探索在帮助学生理解概念上有一定的帮助，但实践发现：相比于这种用一个抽象概念来解释另一个抽象概念的教学方法，对抽象概念进行形象化的类比，更能帮助学生理解，同时也能加深学生的印象.

利用现实生活中的实物或例子，借助数形结合的思想，是帮助学生深入理解基本概念和相关性质的一个有效渠道.实际上，这样的例子在教学中多有存在，如“箭形”行列式、“阶梯形”矩阵等概念，就是借助几何形状和生活实物的类比来直观地描述行列式和矩阵的特点.这些来自于生活的形似化类比可以帮助学生更好地理解知识[9].

本文将针对向量组最大无关组、特征值与特征向量、方阵的相似对角化这三个《线性代数》中的重要知识点，通过生活中的实例开展形似化教学设计，以便学生更加深入透彻地理解相关知识.

2 典型的形似化教学设计案例

2.1 基于任务完成度分析的向量组最大无关组的形似化教学

向量组的最大无关组是线性代数课程《向量组的线性相关性》章节中，在线性表示、线性相关与线性无关等基本概念讲解完成后引入的一个极其重要的知识点，对后续齐次线性方程组基础解系、线性空间的基等概念的理解至关重要，其定义如下[10]：

设A为一个向量组，若A中存在r个向量α1，α2，…，αr，满足：

(i)A0:α1，α2，…，αr线性无关；

(ii)A中任意r+1向量(如果有的话)都线性相关，

那么称部分组A0为向量组A的一个最大线性无关组，r称为向量组A的秩.

依据定义，可以看出最大无关组A0是由向量组A中的r个向量构成的，是A的一个子集，但是这个子集对原向量组A的意义重大.由定义出发，教师通常会引导学生重点关注最大无关组的以下两点基本性质：

(i) 向量组A与最大无关组A0是等价的；

(ii) 向量组的最大无关组A0未必唯一.

与之前的线性表示、线性相关等概念简单明确不同，最大无关组的概念在定义上给出了“存在”、“任意”等逻辑词，学生理解起来会存在一定的模糊，需要教师重点辨析.此时，如果在对概念尚不十分清晰的状态下，进一步讲解上述性质，有些同学理解起来就更加困难了.

如果将向量组A看作是如下图1所示的一个10人团队，那么最大无关组A0则可以看作是这个团队中的一个小组(如2/5/9组成的灰色小组或3/6/8组成的黑色小组)，这个小组是整个团队中的核心，它当中每个成员都非常优秀、不可或缺，是整个团队中的精英小组.现在有一项任务安排给这个10人团队完成，通过对任务的完成度进行分析，可以构建一套形似化教学方案，帮助学生更加清晰地理解最大无关组的上述2条性质：

① 虽然任务是安排给整个团队的，但是往往由于团队中某些成员能力欠缺或态度消极(如图中1/4/7/10号)，使得应当由他们来承担的部分工作不得不由精英小组代为完成.这样一来，精英小组可以完全代表整个团队来完成任务，他们的作用与整个团队的作用是相同的.因此，也就可以理解为向量组A与最大无关组A0是等价的；

② 在一个团队中，这样的精英小组可能不只一个，如图1中的灰色小组和黑色小组他们能力相当，都可以独立完成分配给整个团队的任务，也都可以作为整个团队的代言.因此，这也就可以理解为向量组的最大无关组A0未必唯一.

图1 向量组最大无关组形似化教学设计示意图

2.2 基于树枝分叉结构的特征值与特征向量的形似化教学

特征值与特征向量是线性代数中《矩阵的相似变换》章节中的重要基础概念，其定义如下[10]：

设A=(aij)是n阶方阵，若存在数λ和n维非零列向量x，使得

Ax=λx，

则称数λ为方阵A的特征值，非零向量x为方阵A对应于特征值λ的特征向量.

依据定义可以得到特征值和特征向量的计算方法，即A的全部特征值是其特征方程|A-λE|=0的所有根，而A对应于特征值λi的全部特征向量即为齐次线性方程组(A-λiE)x=0的全部非零解.

上述定义和求解过程可以用图2中示意图进行描述，同时也明确了特征值和特征向量的两条性质：

(i) 若某个非零向量x是A的对应于某一特征值的特征向量，那么它只能对应于这一个特征值；

(ii) 方阵A对应于同一特征值的特征向量有无穷多个(图2中用虚线表示集合含有无穷个元素).

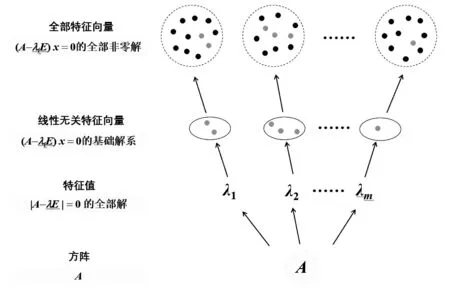
图2 特征值与特征向量求解过程及隶属关系示意图

除了根据定义和求解过程得到上述两条性质之外，事实上，《线性代数》中还证明了关于特征值和特征向量的另外一条重要性质[10]：

(iii) 属于不同特征值的特征向量线性无关.

上述三条性质虽然字面上较易读懂，但学生很难有直观的认识和深入的理解，因此当题目灵活变通时会给他们的解题带来障碍.

为了帮助学生更好地理解，观察图2中的结构：“从方阵A出发——求特征值——求基础解系——求全部特征向量”，这个过程就像一棵树，一级一级地，最终生长为枝繁叶茂的参天大树.因此，我们将图2中的知识逻辑结构形似化为图3所示的树枝分叉图形.图3中的大树，由树干、一级树枝、二级树枝及树叶组成.其中，树干就像是图2中的方阵A，所有一级树枝就是由方阵A这个树干求出的全部特征值，而第i个一级树枝上长出来的二级树枝就可以看作是齐次线性方程组(A-λiE)x=0的基础解系，这些二级树枝及其上的所有树叶便是对应于特征值λi的全部特征向量.在上述形似化类比之下，可以用图3来更加清晰地解释特征向量和特征向量的隶属关系及上述三条性质：

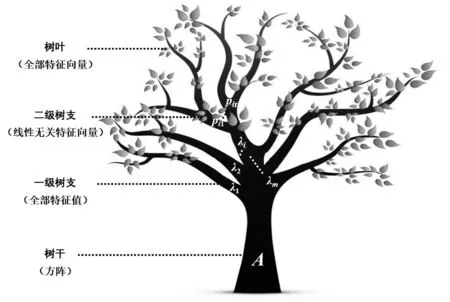
图3 特征值与特征向量形似化教学设计示意图

① 在一棵树上，同一片树叶永远不会隶属于两根一级树枝.类比之下，同一个非零特征向量也永远不会对应于两个不同的特征值，因此A的任一特征向量都只能对应于一个特征值，即性质(i)；

② 对于特征值λi，即第i个一级树枝来说，隶属于它的全部树枝及树叶均由λi的所有二级树枝衍生而来，可类比为：属于同一特征值的全部特征向量是齐次线性方程组(A-λiE)x=0的全部非零解，均由(A-λiE)x=0基础解系(即其全部二级树枝)线性组合而来，因而有无穷多个，此即性质(ii)(当然，由于特征向量不能为零向量，因此在教学中要给学生强调这个线性组合的系数不全为零)；

③ 此外，可将这棵树想得更夸张一点，它的所有一级树枝之间都距离很远，远到隶属于不同一级树枝上的树叶都不可能接触到，则可类比为“属于不同特征值的特征向量线性无关”，此即性质(iii).

树木是我们生活中处处可见的事物，它的“干-枝-叶”结构不仅可以帮助学生形象地理解特征值和特征向量的逻辑关系和重要性质，同时也使学生对知识有非常深刻的印象，对学生的学习大有助益.

2.3 基于分地产粮模型的方阵相似对角化的形似化教学

方阵的相似对角化问题是线性代数课程《矩阵的相似变换》章节中的核心内容.方阵的相似对角化主要包括两个环节：首先，判断该方阵能否相似对角化；其次，在可对角化的前提下，求解相似变换矩阵，完成对该方阵的对角化.实际中，这两个环节是在同一个核心过程中完成的，相关定理如下：

定理n阶方阵A能够相似对角化的充要条件是A有n个线性无关的特征向量.

由定理及其证明过程可知[10]，判断一个n阶方阵能否相似对角化，实际上就是判断它是否有n个线性无关的特征向量：如果没有，则其不能相似对角化；如果有，则可以相似对角化，并且相似变换矩阵就是由这n个线性无关的特征向量为列所组成的矩阵.这个结论简洁清晰，但问题随即转化为：什么情况下n阶方阵能有n个线性无关的特征向量呢？

事实上，关于这一问题有几个重要结论：

(i)n阶方阵A的全部互异特征值λ1，λ2，…，λt可由特征方程求出，其作为特征方程的根的重数ni(i=1，2，…，t)称为该特征值的代数重数.由于特征方程在复数域内恰好有n个根(重根按重数计算)，因此n阶方阵A的所有特征值的代数重数之和必为n，即n1+n2+…+nt=n；

(ii) 齐次线性方程组(A-λiE)x=0的解空间的维数mi，称为特征值λi的几何重数，也是该特征值可以贡献的线性无关特征向量的最大个数.对于方阵A来说，它的每个特征值能贡献的线性无关特征向量的最大个数mi至少为一个，至多则不会超过其代数重数ni，即1≤mi≤ni(i=1，2，…，t)[11]；

(iii)n阶方阵A能否找到n个线性无关特征向量的关键在于其所有特征值的几何重数之和是否为n.结合(i)和(ii)，这可等价地转述为A的每个特征值的几何重数是否都和其代数重数相等，即是否有mi=ni(i=1，2，…，t).显然，代数重数为1的特征值对该问题的答案并无影响，这是因为根据(i)和(ii)的结论，其代数重数跟几何重数必然相等.因此，决定因素在于A的每个代数重数大于1的特征值；

(iv) 如果n阶方阵A的每个特征值的几何重数都等于其代数重数，即mi=ni(i=1，2，…，t)，由于属于不同特征值的特征向量线性无关，因此把所有特征值能贡献的所有线性无关的特征向量合在一起，恰为n个线性无关的特征向量，即m1+m2+…+mt=n，此时n阶方阵A便可以相似对角化；反之，只要有一个特征值的几何重数小于它的代数重数，那么把A的全部特征值能贡献的线性无关的特征向量合在一起，其总数一定小于n，此时A便不能相似对角化.

上述内容结构比较清晰，但逻辑比较抽象，因此一些同学会感觉比较绕，或者感觉结论较多记不住.为了便于学生形象地理解和加深记忆，采用富人分地—产粮这一生活化的例子对其进行了形似化教学设计.如图4，把n阶方阵A看作是一位年老力衰的富人，他有n块大小相同的土地.因为年事已高，他把这n块土地全部分给他的t(t≤n)个孩子λ1，λ2，…，λt去经营.但是富人对这t个孩子的偏爱程度有所不同，因此他在分地的时候并非平均分配，而是分别分给他们n1，n2，…，nt块土地(n1+n2+…+nt=n).接下来，可以通过讨论这t个孩子管理所得土地的产出，来判断富人的家族财富能否得以延续.

图4 方阵的相似对角化教学设计示意图

在这个形似化案例中，拥有n块土地的富人代表n阶方阵A，而他的t个孩子则代表A的t个互异特征值λ1，λ2，…，λt，每个孩子所分得的土地块数n1，n2，…，nt则代表A的每个特征值的代数重数，而这些土地所产出的粮食份数m1，m2，…，mt可看作是相应的几何重数.那么，根据代数重数和几何重数的关系，做出以下两点假设：

① 每块土地不会产出超过1份粮食，因此ni块土地产出的粮食总数mi不会超过ni.这类比于每个特征值的几何重数不会超过其代数重数；

② 仅分得1块土地的孩子都非常勤劳，他们可以保证自己的1块土地能产出1份粮食，而不会更少.这类比于代数重数为1的特征值的几何重数也一定为1.

如此，可以很形象地通过土地的产出来判断富人的家族财富能否延续.显然，如果所有那些被他偏爱的孩子(分得多于1块土地的孩子，亦即代数重数大于1的特征值)没有好吃懒做，都非常努力，其所分得的土地都可以产出相应份数的粮食(代数重数等于几何重数，即mi=ni(i=1，2，…，t))，那么所有孩子产出的粮食合在一起恰好是n份(n阶方阵A有n个线性无关的特征向量).此时，总产出与土地的总块数吻合，即m1+m2+…+mt=n，因此富人的家族财富可得以延续(A可以相似对角化).但是，如果有任何一个被偏爱的孩子所贡献的粮食数量少于他所分得的土地数量(几何重数小于代数重数)，那么粮食总数也一定达不到所有土地应该产出的数量n(A不存在n个线性无关的特征向量)，此时富人的家族财富显然有所缩水，而不能得以延续(A不能相似对角化).

进一步，图4还可以推广到实对称矩阵的对角化问题.不同于普通方阵能否相似对角化是有条件的，实对称矩阵的相似对角化是无条件的，也就是说，实对称矩阵一定可以相似对角化.在图4的框架下，可以形象地将实对称矩阵看作一位所有孩子都很有能力、很争气的富人，他的每一个孩子都能让手里的土地产出相应数量的粮食.因此实对称矩阵这位富人，不必像普通富人一样，担心家族财富缩水，也就是一定可以相似对角化.

富人分地-产粮这种生活化的例子，可以帮助学生更加形象地理解方阵相似对角化的条件，同时能够特别加深学生的印象，使学生对知识的记忆更加牢固，从而提高教学质量.

3 形似化教学设计实践效果

形似化教学在帮助学生理解和固化知识方面有非常大的作用.为了能够定量地展现其优势，在教学中采用上述形似化教学范例时，均设计了相关试验.试验的基本过程如下：首先，在往年练习和考试的题库中提前选择了10道相关知识点的题目，其中1-8题难度接近，属一般难度，9-10题难度接近且难度稍高.将10道题目随机分为A、B两组，每组5道题，其中均包括一道难度稍高的题；其次，在已传授知识点但未引入形似化案例时，将A组题目发布给学生进行解答；再次，在引入形似化案例之后，将B组题目发布给同一批学生进行解答；最后，对A、B组题目的答题情况进行统计分析.统计结果如图5所示，其中范例1表示特征值与特征向量教学试验，范例2表示方阵的相似对角化教学试验.经统计对比发现，使用了范例1和范例2进行形似化教学后，学生5道题目的平均错误率均明显降低，分别由21%和28%下降到9%和12%，尤其对于难度较大的题目，错误率下降更加明显，分别由27%和32%下降到12%和14%，这说明形似化范例的引入使得学生更能厘清知识的深层逻辑结构，能帮助学生从本质上理解和记忆知识，因此相对于引入形似化案例之前，学生更能应对题目难度的增加，解答也更有把握.

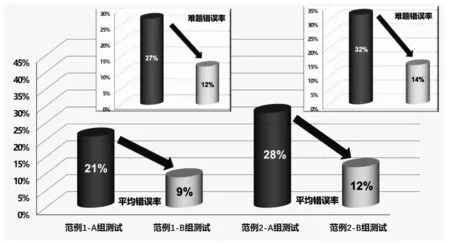
图5 形似化教学试验结果

此外，作者自2018年开始对形似化教学进行系统性、规范性研究，形成了若干形似化教学范例，并将之应用于《线性代数》教学中，取得了良好的实践效果.图6列出了2017-2019年的学生成绩，可以看出引入了形似化教学设计后，学生的整体成绩得到明显改善：优秀学生(90分以上)的比例由2017年的13.1%增长至2019年的29.3%，2019学年80分以上的学生比例接近60%；同时，自引入形似化教学设计后，不及格学生的比例明显下降，由2017年的21.2%下降至2018和2019年的12%左右.这些数据证明了形似化教学设计对学生理解《线性代数》课程中抽象复杂的内容具有积极有益的作用.

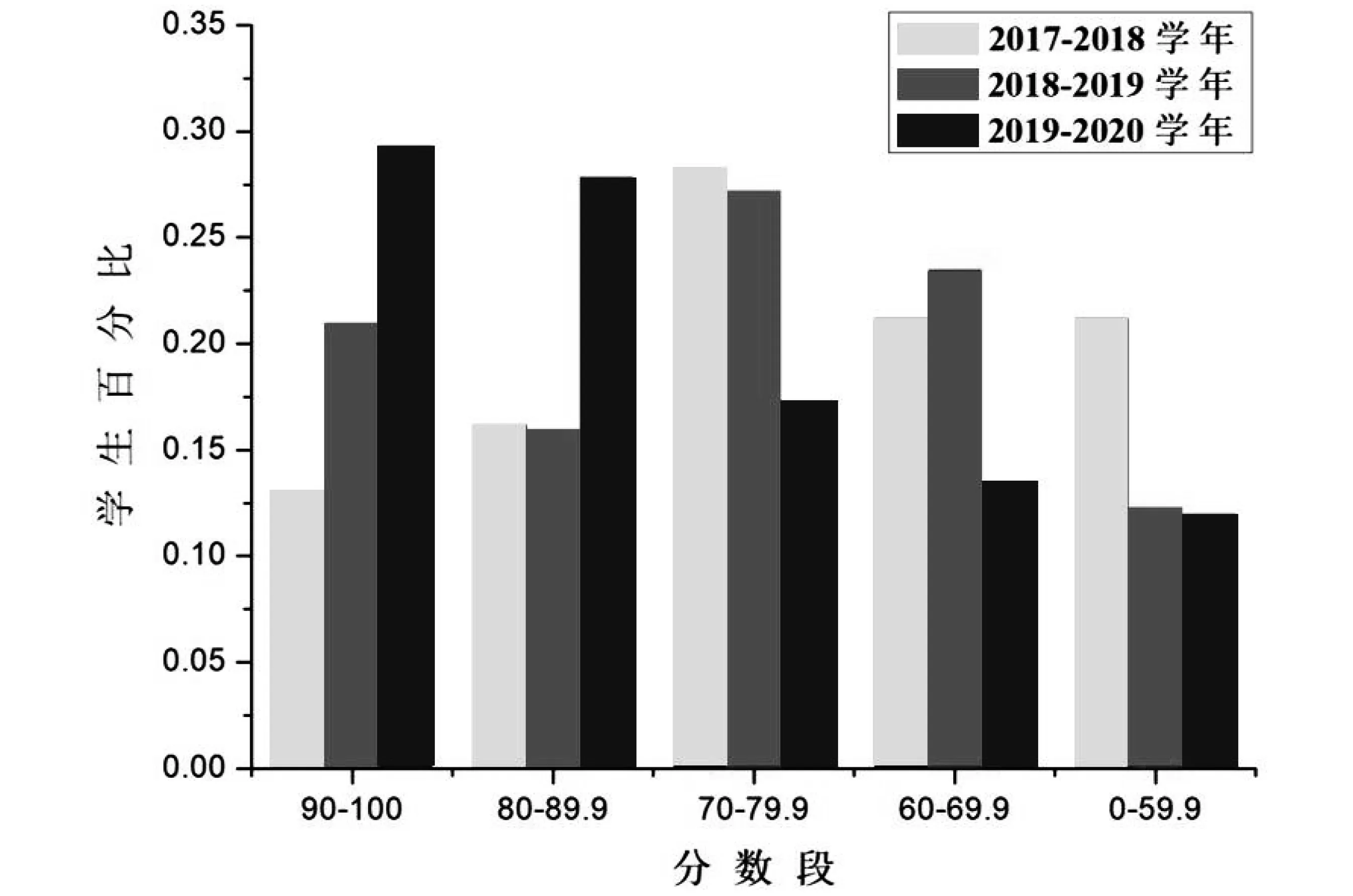
图6 2017-2019年分数段统计图

4 结 论

形似化教学设计可以帮助学生更加深入透彻地理解知识，同时加深印象、强化记忆，促进知识内化.本文给出了《线性代数》中三个形似化教学范例，实践表明这种形似化教学范例可以有效地帮助学生明晰概念的内涵和逻辑关系，提高教学质量.此外，形似化教学设计思想也具有良好的可复制性，可以在其他课程当中予以应用和发展.

致谢感谢参考文献给予本文的有益启发及审稿专家们的宝贵意见.