简单随机抽样的一个注记
董俊超
(烟台大学 数学与信息科学学院, 山 烟台264005)
1 引 言
简单随机抽样是抽样调查课程中最简单的一种抽样方法,因为其在实践中操作简单,所以使用最为广泛.关于它的定义一般有两个:一个是基于全样本过程(whole sample procedure)的抽样(见下文定义1),另一个是基于逐个抽取不放回过程(draw-by-draw without replacement procedure)的抽样(见下文定义2).关于这两个定义的关系, 国内一般的教科书及一些专著,比如冯士雍等[1],杜子芳[2],孙山泽[3]的著作中都略有论述.本文的目的则是更详尽地讨论它们的关系,说明在一定意义下,它们是等价的;在另外的意义下,它们是不等价的;同时指出也可以有其它的方法来实现简单随机抽样.
另外需要指出的一点是,在一般的《数理统计》教课书中所说的抽样方法是放回的简单随机抽样,而在抽样调查课程中所说的抽样方法要多很多.现在越来越多的人都在用抽样调查的方法来研究实际问题,比如孙华娟等[4],胡良剑等[5]就用抽样调查方法来研究问题.
2 变概率抽样可作为简单随机抽样的例子
为了下面叙述的方便,把冯士雍等[1]著作中的定义叙述如下:
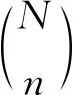
定义2[1]从总体的N个单元中,逐个不放回地抽取单元,每次抽取到尚未在样本(未入样)中的任何一个单元的概率都相等,直到抽足n个单元为止,这样所得的n个单元组成一个简单随机样本.
为了区分定义1与定义2,不妨称定义1中的简单随机抽样为基于全样本过程(whole sample procedure)的简单随机抽样;定义2中的简单随机抽样为基于逐个抽取不放回过程(draw-by-draw without replacement procedure)的简单随机抽样.
一般的统计学课程中考虑的是无序样本,只要样本的分布是一样的,这样的抽样就认为是等价的.因此从这个意义上讲,由于基于全样本过程(whole sample procedure)的简单随机抽样(定义1)与基于逐个抽取不放回过程(draw-by-draw without replacement procedure)的简单随机抽样(定义2)所得的样本分布是一样的,可以说这两个定义是等价的.这个在在冯士雍等[1]中已有说明.
但是从另外意义上来讲,抽样调查不仅要考虑样本的分布,还要考虑抽样过程的设计,因为利用抽样过程所包含的信息可以设计出更好的估计量.这个在著作[1]中的第五章中就有论述,更详尽的论述可参看MURTHY[6]及DES R[7].定义1得到的是一个无序样本,它只说明了最终的样本分布,而不包含抽样的过程;而定义2得到的是一个有序样本(尽管我们不考虑它的顺序),它不仅包含抽样的过程,还有与定义1有相同的样本分布.定义2包含的信息比定义1包含的信息要多,所以在这个意义下,不能说定义1与定义2是等价的.
为了更清楚地说明这一点, 不妨借助于变概率抽样(varying-probability sampling) 这个概念来说明变概率抽样也可以实现定义1中的简单随机抽样.关于变概率抽样,文献中并没有给出精确的说法, 只有一个比较笼统的说法,比如在戈文达拉玉卢[8]中略有介绍.为了下面说话方便, 给出一个精确性的定义:
定义3在由N个单元组成的总体中,逐个从总体当中抽取单元(可以是放回抽样也可以是不放回抽样);如果至少有一次在抽取尚未在样本中的单元时,它们被抽到的概率不都相等,直到抽足n个单元为止,则这样的一种抽样方法称为变概率抽样(varying-probability sampling).
定义3实际上就是与定义2相对立的概念, 即不满足定义2的概念我们称为定义3(在不放回抽样时). 下面将说明,变概率抽样也可以满足定义1.
用pi表示逐个抽样抽取第一个样本单元时,第i个单元被抽到的概率;用pj|i表示抽取第二个样本单元时,在第1次抽到第i个单元的条件下第2次抽到第j个单元时的概率;其它记号以此类推.
现考虑一个从由N=4个单元组成的总体中,抽取容量为n=2的一个样本,pi及pj|i(i,j=1,2,3,4;i≠j)的定义分别见表1及表2.

表1 pi的值

表2 pj|i的值
显然上面定义的抽样是一个变概率抽样,因为无论是抽取第1个样本单元还是抽取第2个样本单元,抽取它们的概率并不都相等;现计算任意一个样本{i,j}被抽中的概率p(i,j):
p(i,j)=pipj|i+pjpi|j,i≠j;i,j=1,2,3,4.
分别计算之,比如
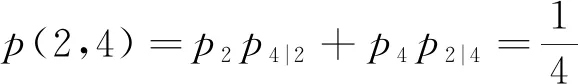
注1 定义2只是定义1的一个实现;变概率抽样也可以是定义1的一个实现.
3 进一步的讨论
对于抽样设计,除了前面提到的全样本方法(whole sample procedure),逐个抽取不放回方法(draw-by-draw without replacement procedure)外;还有逐个抽取放回方法(draw-by-draw with replacement procedure).逐个抽取放回抽样也可以实现定义1的简单随机抽样,见SAMPFORD M R[9], 不再讨论.
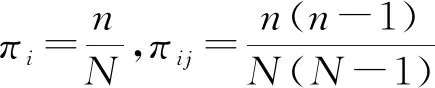

表3 总体容量N=6样本容量n=3的一个抽样分布
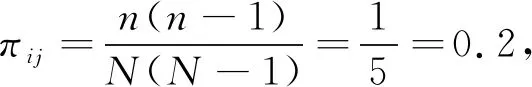
π12=P{1,2,3}+P{1,2,4}+P{1,2,5}+P{1,2,6}=0.04+0.03+0.04+0.09=0.2,
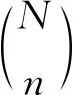
注2 不等概率抽样(定义4)也可以有与满足定义1抽样一样的性质(限于一阶矩及二阶矩).
由此,不妨给出简单随机抽样的更具一般性的(广义)定义:
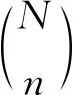
4 结束语
本文给出了变概率抽样(定义3)以及广义简单随机抽样(定义5)的定义.指出了不仅基于逐个抽取不放回过程(draw-by-draw without replacement procedure)的简单随机抽样(定义2)可以实现基于全样本过程(whole sample procedure)的简单随机抽样(定义1),而且变概率抽样(定义3)也可以实现基于全样本过程(whole sample procedure)的简单随机抽样(定义1);基于一阶矩及二阶矩,不等概率抽样(定义4)也可以实现基于全样本过程(whole sample procedure)的简单随机抽样(定义1).但变概率简单随机抽样在实际当中很难操作,它只是一个理论结果,实际当中的简单随机抽样还是用定义2所确定的简单随机抽样.本文的结论只是对简单随机抽样理论的一个补充,希望对有关人员有所裨益.
致谢作者非常感谢审稿专家提出的宝贵意见,使得本文的论述更加清晰,准确.

