基于B样条的函数型数据表示与配准
孙 萍, 刘源昊, 王旭辉
(合肥工业大学 数学学院,合肥230601)
1 引 言
函数型数据概念最初是由J. O. Ramsay[1]和C. J. Dalzell[2-3]提出的.函数型数据是指在紧区域上实值函数的实现,其将观测到的离散数据当作一个整体来考虑.从函数型数据角度,可用一个连续的函数来表示观测数据,即离散数据来自一条光滑的曲线.
在函数型数据分析中,大多数样本函数都呈现出典型的形状特征序列(例如峰和谷),如著名的伯克利生长数据集[4-6],为研究生长曲线的形状特征,Laura M. Sangalli[7]、Yu-Hsiang Cheng[8]等人引入了曲线配准方法来聚类和对齐生长曲线.该方法允许振幅和相位变化的分离,来研究生长的阶段性特点与生长曲线形状特征.振幅和相位为曲线的形状特征,相位变化由扭曲函数(warping function)表示.
通过曲线对齐和扭曲函数复合来消除相位变化的过程称为曲线配准[9].配准的目的是分解函数型数据曲线样本的幅度和相位变化.相位变化通过扭曲函数捕获,扭曲函数单调的变换函数域[10].配准后的曲线应仅显示振幅的变化,使曲线特征突出.文献[11]中主要讲述了函数数据的配准或注册的特定方面,讨论如何处理两个或多个函数的配准问题,提出将扭曲函数作为工具,以水平调整观察到的函数,减少它们的方差.数学上,研究2D、3D和更高维度的曲线形状,通过配准使函数形状的波峰波谷对齐,为研究函数形状带来便利,因此配准问题对函数型数据的形状分析至关重要.
曲线配准问题已被国内外许多学者研究.A. Kneip(1995)等[12-13]深入研究了标志配准,将标志称为结构性特征,位置称为结构点;作为标志配准的替代方法,Silverman(1995)[14]开发了一种不需要对标志进行解释的曲线配准技术.D. Telesca (2008)等[15]提出了贝叶斯层次曲线配准新模型.O. Collier (2015)等[16]提出了一个非参数测试框架,其中开发了广义似然比测试以执行曲线配准.Aishwarya Pawar (2019)等[17]提出一种基于动态水平集(使用截断的分层B 样条)的联合图像分割和配准.
本文将函数型数据用B样条基函数拟合,充分利用了B 样条基函数自由度高,灵活性强等特点[18-21].并构造曲线配准能量项作为标准,从而寻找扭曲函数对拟合后曲线进行曲线配准.需要指出的是,为了将整个函数型数据配准问题统一在B样条函数框架上,扭曲函数也选择为B样条函数.
2 基于B样条的函数型数据配准问题
2.1 函数型数据的近似表示
一个随机变量在无穷维空间或函数空间取值,则称其为一个函数型变量[22],称其观测值为函数型数据,函数型数据一般以离散数据的形式存在.对一个连续的函数过程,将其表示为{f(t),t∈I},一维情形时,I⊆1,二维情形时,I⊆2.容量为N的样本记为fi(t),i=1,2,…,N,它们独立且与f(t)同分布[23]. 观测到数据对(tij,fi(tij)),其中tij,j=1,2,…,ni为观测点,且对函数fi(t)观测ni次.获得的数据对为离散数据,随着函数个数和观察次数的增加,函数数据趋于无穷维.故在函数型数据分析过程中,函数具有高维的特征,需要对函数型数据进行降维.常见的方法是利用基函数表示函数型数据[24].设有一组基函数φi(t),i=0,…,l,则函数f(t)在函数空间span{φ0(t),φ1(t),…,φl(t)}上的估计可表示为
(1)
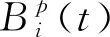
其中k=1,2,…,p. 特别地,当p=3时,U=[u0,u1,…,un+4].为了保证端点插值性质,取
u0=u1=u2=u3,un+1=un+2=un+3=un+4,
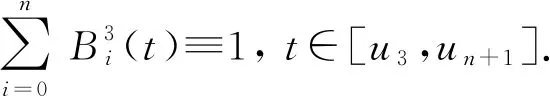
系数ci,j,j=0,…,n可由最小二乘法计算,即
(ci0,…,cin)T=(ATA)-1(fi(t0),…,fi(tn0))T,
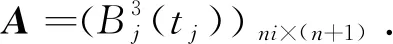
2.2 函数型数据的曲线配准问题
则
故本文中,不妨设给定函数f1(s),f2(t),s,t∈[0,1]. 成对配准问题是指寻找恰定的扭曲函数t=γ(s),使f1,f2∘γ在某种意义下误差极小.即
(2)
其中E为某种能量函数,Γ为满足一定条件的函数集合.函数γ(s)须满足:
(i)γ∶[0,1]→[0,1];
(ii)γ(0)=0,γ(1)=1;
(iii)γ可逆,且γ和γ-1为光滑函数.
设ΓI表示所有满足条件(i)-(iii)的函数集合,I为γ的定义域.可知ΓI是一个李群[11],即对任何γ1,γ2∈ΓI,有群算子(γ1∘γ2)(s)=γ1(γ2(s)).一般情况下,可将能量函数取为L2范数,即问题(2)转换为
(3)
文献[11]提出一种动态规划算法用于解决式(3)中所述的最小化问题,该动态编程算法通过动态调整离散参数格点方法得到扭曲函数.
由2.1节的函数型数据表示方法,可设f1(s),f2(t)的B样条函数近似为
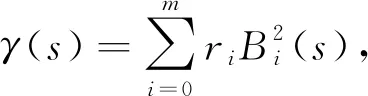
(i′)γ(s)的节点序列为V=[0,0,0,s3,…,sm,1,1,1],其中s3>0,sm<1,si+l>si,i=3,…,m-1;
(ii′)r0=0,r1=1,ri≤ri+1,i=0,…,m-1.
根据样条函数的性质[27],条件(i′) (ii′)保证了γ(s)满足条件(i),且在区间[0,1]上单调递增,进而为可逆函数,此外γ(0)=0,γ(1)=1. 记满足条件(i′) (ii′)的2次B样条函数为Π. 则在B样条的表示框架下,成对函数型数据的匹配问题(3)可转换为极小化问题:
(4)
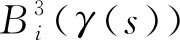
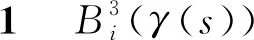
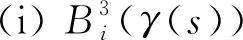
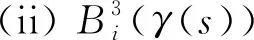
证由于复合函数的n阶导函数公式为

下面给出定理1的一个算例.

例1给定节点向量U=[0,0,0,0,1/3,2/3,1,1,1,1],定义在U上的三次B样条函数为
其中c0=0,c1=2,c2=3,c3=1,c4=2,c5=0. 扭曲函数γ(s)为
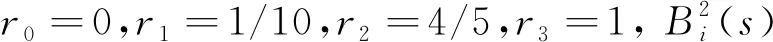
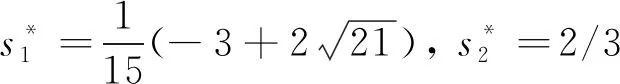
(5)
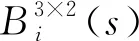
2.3 曲线配准的算法步骤
根据上述的分析,给出基于B样条的曲线配准的具体步骤如下:
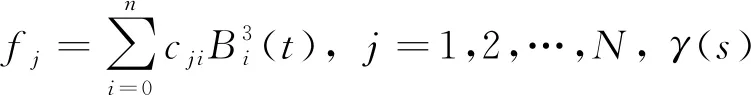
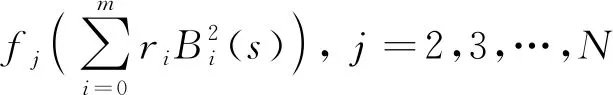
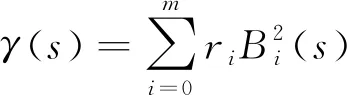
3 算例研究
为验证本文算法的有效性,分别用文献[30]中使用的数据和fdasrvf库函数中的数据运行算法.通过调整函数参数获取多组数据进行验证本文算法,例如算例2-4来自同一函数拟合数据.
例2一组函数由下式给出:
yi(t)=zi,1e-(t-1.0-λ1)2/2+zi,2e-(t+2.0-λ2)2/2,t∈[-3,3],i=1,2,…,N.
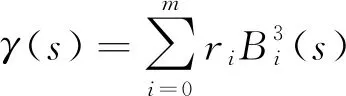
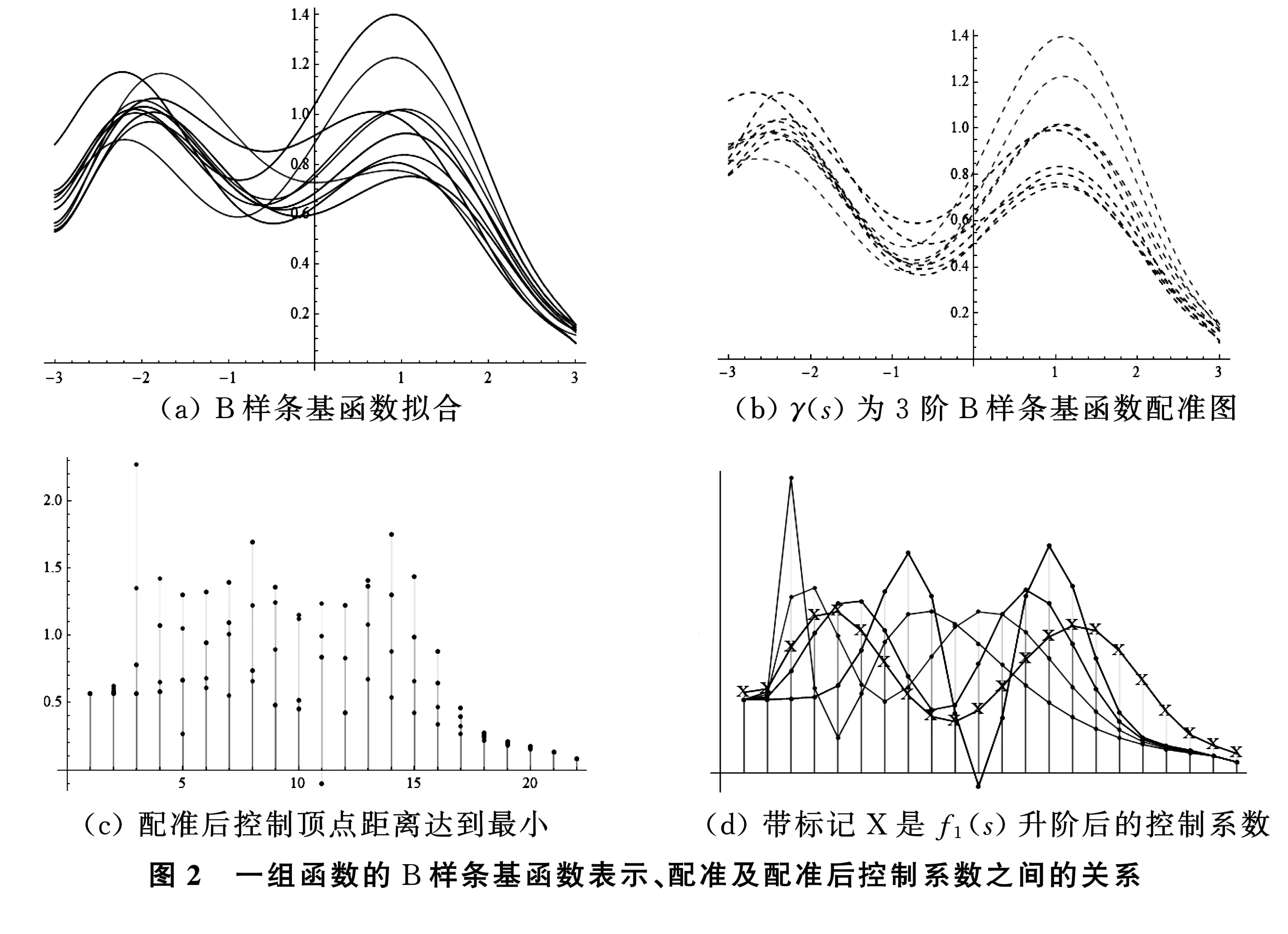
对于上述有明显极值点的函数,可以比较极值点的方差,计算原始函数配准后极值点方差分别为0.00786645,0.0315444,0.00883703,配准前极值点方差分别为0.0250637,0.084134,0.0140217.极值点的方差配准后明显减小,配准后函数在波峰和波谷一定程度集中,即函数配准有明显效果.
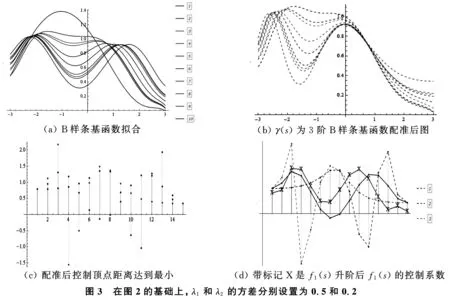
例3对于例2,可以通过改变zi,1和zi,2的均值和方差或改变λ1和λ2的均值和方差来改变形状,在保持其他不变的情况下,将λ1和λ2的方差分别设置为0.5和0.2.其与图2相对应的图形如图3.通过计算,配准后的L2距离小于配准前的L2距离,配准效果显著.图3d中蓝色实线带标记X表示升阶后f1(s)的控制系数的折线图,图3c中配准函数的控制点与f1(s)升阶后的控制点距离达到最小.
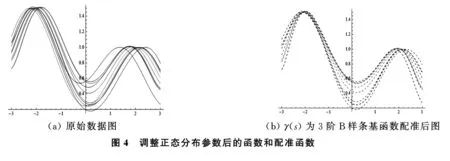
例4调整例2中λ1,λ2正态分布参数,图4a表示调整后的函数,图4b是其配准后的函数,配准后的极值点方差分别为0.00322853、0.000136298、0.022294,配准前的极值点方差分别为0.0294151、0.0187822、0.0891169,极值点的方差明显减小,可以判断配准后函数在波峰明显较配准前集中.计算函数配准前后的L2距离,配准后整体呈减小趋势.
例5从fdasrvf库函数中获取模拟数据集,图5a为原始数据B样条拟合后的形状,图5b中虚线是3阶B样条基拟合γ(s)与图5a函数配准后结果.调整拟合γ(s)的B样条阶数,图5c、图5d分别为4阶、5阶B样条基拟合的γ(s)与原始函数配准结果.
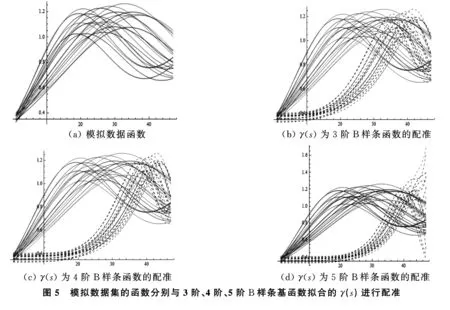
通过计算配准前后的极值点方差和配准前后函数与f1(s)的L2距离,可以得到,函数配准后的极值点方差都是减小的.当γ(s)是3阶的,其配准前后的极值点方差分别为32.3751,7.50638;当γ(s)是4阶的,其配准前后的极值点方差分别为32.3751,4.63976.当γ(s)是5阶的,配准后的函数形状趋于离散,极值点的范围更广,无法确定极值点.随着γ(s)阶数的增加,配准后函数在一定程度较配准前更集中,但γ(s)的阶数并不是越大越好.
通过算例验证分析,得出以下几点结论:
4 结 论
针对基于B样条的函数型数据配准问题,本文结合B 样条基函数拟合函数型数据,扭曲函数γ(s)同样基于B样条函数,配准后的函数相当于对原函数升阶,将配准函数与原始直接升阶的函数f1(s)进行比较.
(1) 基于B样条函数拟合的函数型数据,对其进行函数配准,扭曲函数γ(s)满足B样条基函数结构,函数配准后使其在波峰波谷更集中;
(2) 在函数型数据的配准算例中,扭曲函数γ(s)的B样条基的次数对配准函数有一定影响.一般情况是越大越好,但到特定阶之后,γ(s)的阶数越高,使得γ(s)中的参数越多,配准后函数阶数也就越高,函数过于平滑,影响函数的配准效果.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

