以算法为核心的信息安全数学基础教学体系探索与实践
聂旭云, 陈大江, 熊 虎
(电子科技大学 信息与软件工程学院,成都610054)
1 引 言
自从2017 年教育部高教司发布“关于开展新工科研究与实践的通知”以来,面向新工科的教学改革成为当前改革的重点[1-2].新工科人才培养模式注重更新人才培养理念、重构培养目标和知识结构、转变培养方式等[3].教育部《普通高等学校本科专业类教学质量国家标准》指出,大学生本科专业教育质量评价要突出学生中心、产出导向和持续改进,其中产出导向(outcomes-based education,OBE)是指教学过程和结果不能仅以知识传授为重点,而更应注重学生能力的培养[1].目前,以OBE 为核心理念来指导教学目标设计、改进教学过程、完善评价方法已经成为面向新工科的课程教学改革的主要方向.OBE 理念要求课程大纲制定要体现学生学习目标以及如何通过有效评价来保障学生达到学习目标.随着工程教育认证的全面推行,推进面向新工科的软件工程专业课程教学改革,重新确定课程目标与内容,并将以学生为中心和面向产出的教学实践落到实处,这是目前教学活动中迫切需要解决的问题[3].
信息安全数学基础是网络空间安全专业的必修基础课程,一般开设在大二上学期.它的内容涵盖数论、抽象代数中的整除、同余、群、环、域等理论.课程内容涉及大量的概念、性质和理论方法,作为工科大二学生学习这些知识有一定的难度.人们对如何提高信息安全数学基础的教学效果进行了大量的探索[4-9],但多数改进方法都是围绕着理论教学进行.教师若仅采用传统授课方法,注重概念的讲解和理论的推导,那么教学过程就会比较枯燥,学生的学习兴趣也会大大降低.电子科技大学软件工程(互联网安全)专业,遵循工程教育认证和新工科教育的理念,参考其他院校的先进经验[10],探索并实践了以算法为核心的信息安全数学基础教学体系,对课程目标和所支撑的毕业要求进行了梳理,按照以算法为核心的教学思路,改进了课程教材[11],提出了相应的理论与实践教学模式,培养学生的实践能力和创新能力[12].
2 教学探索
2.1 课程目标
课程目标的制定应该自顶向下,从专业培养目标和毕业要求的角度出发确定具体的教学目标,其中最为关键的一点是观念转变,课程目标制定的出发点要由“教师想教什么”转变为“学生需要学什么”.其次,课程目标的分解应该使得教师能够更好地对课程目标的达成度进行评价[2],应由传统的横向分解转变为纵向分解,这也是基于OBE 课程教学改革的重要举措.
信息安全数学基础课程在电子科技大学软件工程(互联网安全)专业的整个课程体系当中所支撑的毕业要求指标点具体为“能够采用科学的方法对软件系统中的关键环节,设计相应的实验方案,搭建实验环境,开展实验”.为了后续密码学、网络安全协议等课程的顺利学习,本课程要求学生掌握各类代数系统的结构及其元素运算的方法,搭建各类密码算法和密码系统实现的实验环境.
在2016年的信息安全数学基础教学大纲中,课程目标的分解是按照知识点的深入进行的,如下所示:
CO1:对信息安全的基础概念、基本数学方法等有一个基本了解,掌握数论基础知识;
CO2:掌握信息安全技术中的核心数学算法,数学环境构造方法,掌握近世代数基础知识;
CO3:建立对信息安全技术的整体概念,了解经典信息安全算法的数学困难问题;
CO4:了解信息安全基础算法,掌握安全性证明中的基础数学问题及方法.
上述分解更多的是从理论学习上去解构信息安全数学基础的知识,不能很好地对毕业要求指标点的达成起到支撑作用.因此,在2019年,课程组将课程目标分解如下:
CO1:掌握密码算法中的数论和抽象代数的基本概念和性质;
CO2:掌握各类代数结构如整数模n剩余类环、模多项式剩余类环、有限域等的构造方法和运算规则;
CO3:掌握密码算法实现的关键环节即数学基础算法的原理,如数论中的大整数运算、模指数运算、有限域运算等;
CO4:根据算法原理,设计实验方案,掌握并实现信息安全数学基础相关算法.
从上述课程目标纵向分解可以看出,本课程的课程目标是递进式、可独立评估的,可以将具体教学内容、教学环节以及教学评估与课程目标直接关联,同时课程达成度的评价也为本课程所支撑的毕业要求指标点的达成度评价提供了依据.
2.2 课堂教学设计
信息安全数学基础核心知识分为两大部分:数论和抽象代数.这两部分内容关联紧密,不可分割.通过数论中的实例来理解抽象代数中群、环、域的概念,反之,利用抽象代数中的理论来简化数论中相关定理的证明,从而促进学生更好地理解这些数学理论.经过多年的教学实践,发现工科学生对如何实现数论和抽象代数中的相关算法更感兴趣.通过实现这些数学算法,可以更容易地实现现有的密码算法.因此,课程组围绕RSA加密算法和ElGamal加密算法的基本原理和实现方法组织了教学内容,并将数论和抽象代数这两部分通过从n到p的演化联系起来.
2.2.1 数论教学内容组织
本课程数论部分的教学从分析RSA公钥加密算法出发,利用问题导向的方式引入数论相关知识,结合RSA公钥密码算法的实现过程,熟悉并掌握相关的数学算法.RSA是目前最常用的一类公钥密码算法.通过RSA算法的实现,可将数论部分的知识点和相关算法串联起来.以RSA公钥加密算法为例,算法可分为两部分,一是密钥生成,二是加密和解密.
根据RSA的安全性要求,其公钥长度至少为1024比特,这个长度已经远远超出了程序语言中的长整型的表达范围,因而需要建立多精度数整数计算环境.从密钥生成算法中可以看出,首先要产生两个大素数p和q,来得到正整数n.由于素数的分布规律性不强,因此需要采用素性检测算法来生成,一般推荐使用Miller-Rabin素性检测算法.公钥的生成需要求模φ(n)下的逆元,这就需要用到扩展的欧几里得算法.
在RSA加密过程中,加密和解密均需要用到大整数的幂运算,因此可采用重复平方乘算法、蒙哥马利算法提高其效率.更进一步,在解密过程中,因为模数n=pq为两个素数的乘积,因此可用中国剩余定理来加速其解密过程.
综上所述,实现RSA算法需要掌握和理解的算法主要有多精度数运算、扩展的欧几里得算法、素性检测、大整数模幂运算以及中国剩余定理等,如图1所示.

图1 RSA算法实现所涉及的知识点和算法
因此,数论部分从整除概念出发,引出最大公因数、素数的概念,通过带余除法给出多精度整数的表示以及相应的加减乘除算法,同时通过整除和带余除法给出同余的概念,进而构造模整数的剩余类集合,讨论该集合及元素的性质,给出模整数的幂运算加速算法以及解同余方程的中国剩余定理等.这里重点要掌握的算法是多精度数运算、扩展的欧几里得算法、素性检测、重复平方乘算法以及中国剩余定理算法,如图2所示.
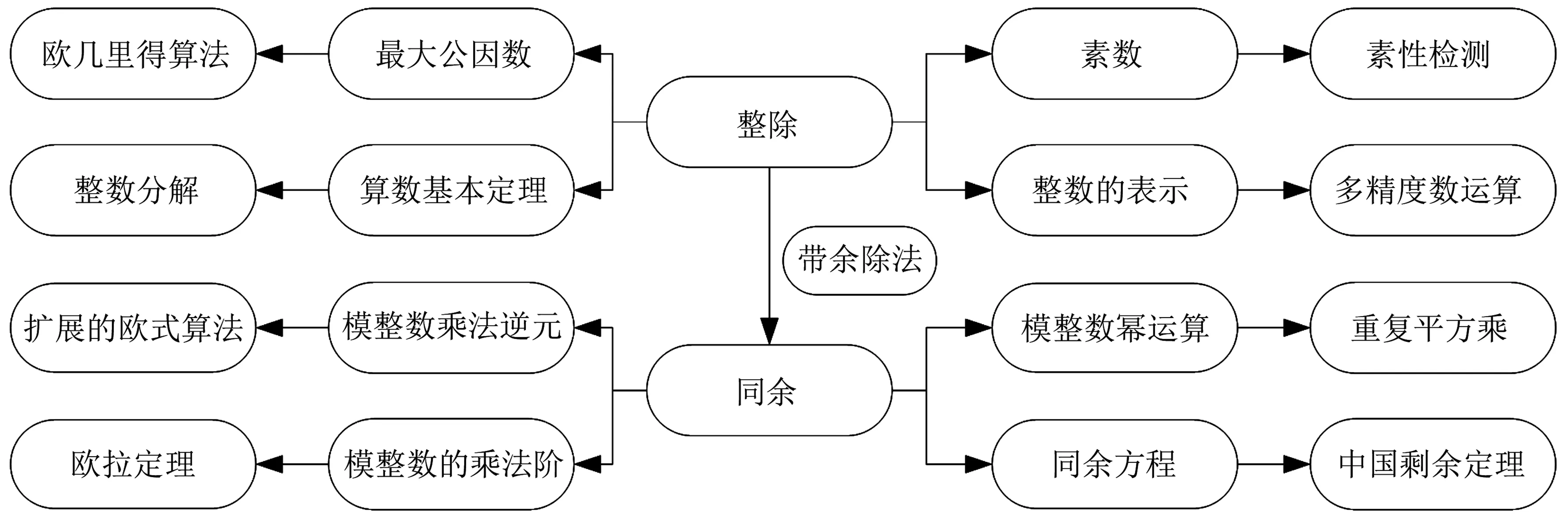
图2 数论部分主要知识点及相关算法
2.2.2 抽象代数教学内容组织
本课程抽象代数部分从分析有限域上的ElGamal公钥加密体制出发.这里稍微对传统的ElGamal加密算法做了改动.传统的ElGamal加密算法是定义在有限域p上的,由于教学需要,课程组将ElGamal加密算法推广到p的扩域Fpn上.ElGamal加密算法也分为两部分,一是密钥生成,二是加密和解密.为了实现一个Fpn域上的ElGamal加密体制,首先要建立好算法的计算环境,即要构造出Fpn域,定义其加法、乘法和求逆运算,这里需要用到多项式同余、多项式求逆(扩展的欧几里得算法).其次要找到域Fpn中的乘法群的生成元,这里需要利用到循环群中元素的阶的判定及寻找生成元的算法.最后,计算公钥还需要使用重复平方乘算法.运算环境搭建好之后,加密和解密算法仅涉及到用重复平方乘算法来计算幂运算以及用多项式扩展的欧几里得算法来求元素的逆.如图3所示.

图3 ElGamal算法实现所涉及的知识点及算法
因此,抽象代数部分由分析整数集合和整数模n剩余类集合出发,引出群、环、域的定义和性质,给出循环群的结构,理想和剩余类环的定义及性质等.构造素域上的多项式环,类似于整数集合当中的整除和同余理论,给出相应的概念和理论分析,如带余除法、最大公因式、不可约多项式、多项式同余等.在多项式环的基础之上,给出有限域的构造,包括元素的表示方法、运算规则等.这里重点要掌握的是循环群的生成元的寻找算法、多项式相关算法(如多项式的加减乘除、同余求逆等)、有限域中元素的运算算法等,如图4所示.
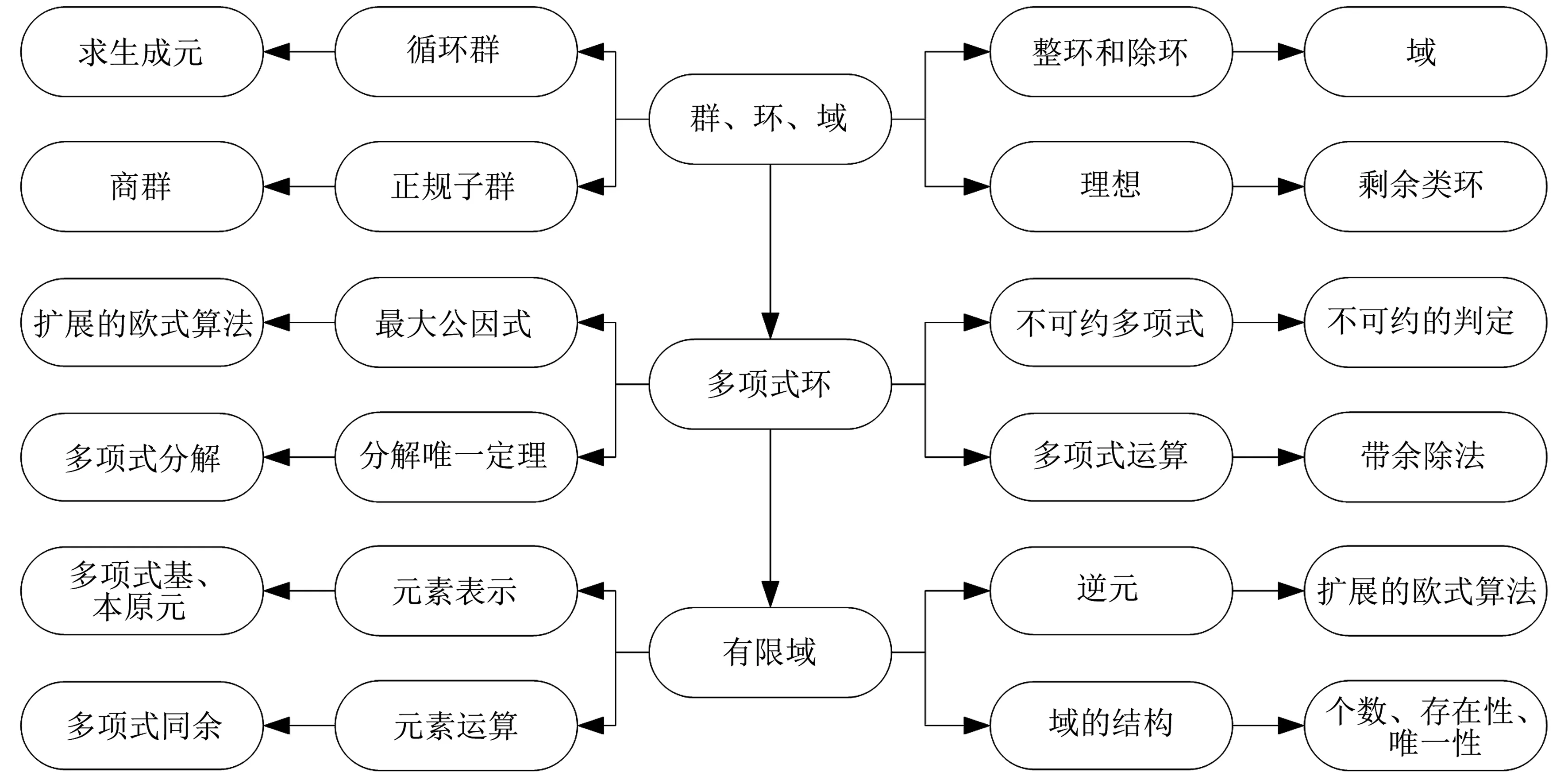
图4 抽象代数部分主要知识点
2.3 实践教学体系设计
信息安全数学基础的实践教学遵循由点及面、循序渐进的原则,首先利用课程实验搭建必要的实验环境,如大整数运算环境、有限域运算环境等,其次,利用综合课程设计将课程内容和主要知识点串联起来,并采用研讨的方式,扩展教学内容,为进一步参加创新项目和学科竞赛奠定基础.
课程实验的主要目的是培养学生设计实验方案,搭建实验环境,开展实验的能力.本课程的课程实验一共4个算法,8个学时.这4个算法分别为多精度整数运算算法、模大整数重复平方乘算法、多项式扩展的欧几里得算法和有限域的运算算法.课程实验采取实验室集体教学,提交实验报告作为考核依据.
电子科技大学软件工程(互联网安全)专业的综合课程设计是独立的实践教学环节,层次递进,前后衔接,分为综合课程设计I、II、III,分别在第三、四、五学期执行[13].信息安全数学基础的综合设计属于综合设计I阶段,是专业大二上学期学生的必修环节,其主要目的是培养学生进行分析文献、选择解决方案的能力.课程组选择RSA加密算法的实现和有限域上ElGamal加密算法的实现作为综合设I的题目.综合设计I题目发布后,学生自由组队,一般4-6个学生一组.综合设计采取课下讨论形式完成.指导教师在综合课程设计开展之前,需要制定任务书,给出总体要求、实施建议和预期成果等.综合课程设计开展初期,学生在教师的指导下进行相关文献查阅和研讨,制定工作计划,完成小组分工,提出重点要解决的问题和可能的解决方案.在综合课程设计实施过程中,教师和小组成员定期进行讨论,以学生为主导,指导教师参与,给出进展建议,协助解决关键技术问题.
2.4 课程考核评价设计
课程评价分为两个部分,一是课程目标达成评价,二是毕业要求达成评价.
课程的四个课程目标在整体评价中分别赋予相应的权重,然后根据期中测试、期末考试和实验报告来综合评价.期末考试试题分别从概念、结构和算法三个层面来考察学生的掌握情况,课程实验评价依据由实验报告给出实验成绩,共分为4个部分:实验目的及原理、实验内容及步骤、实验结果及分析以及实验报告质量.对课程目标和毕业要求指标点的达成主要通过实验报告前三个部分评价来支撑.
课程目标评价如表1所示:
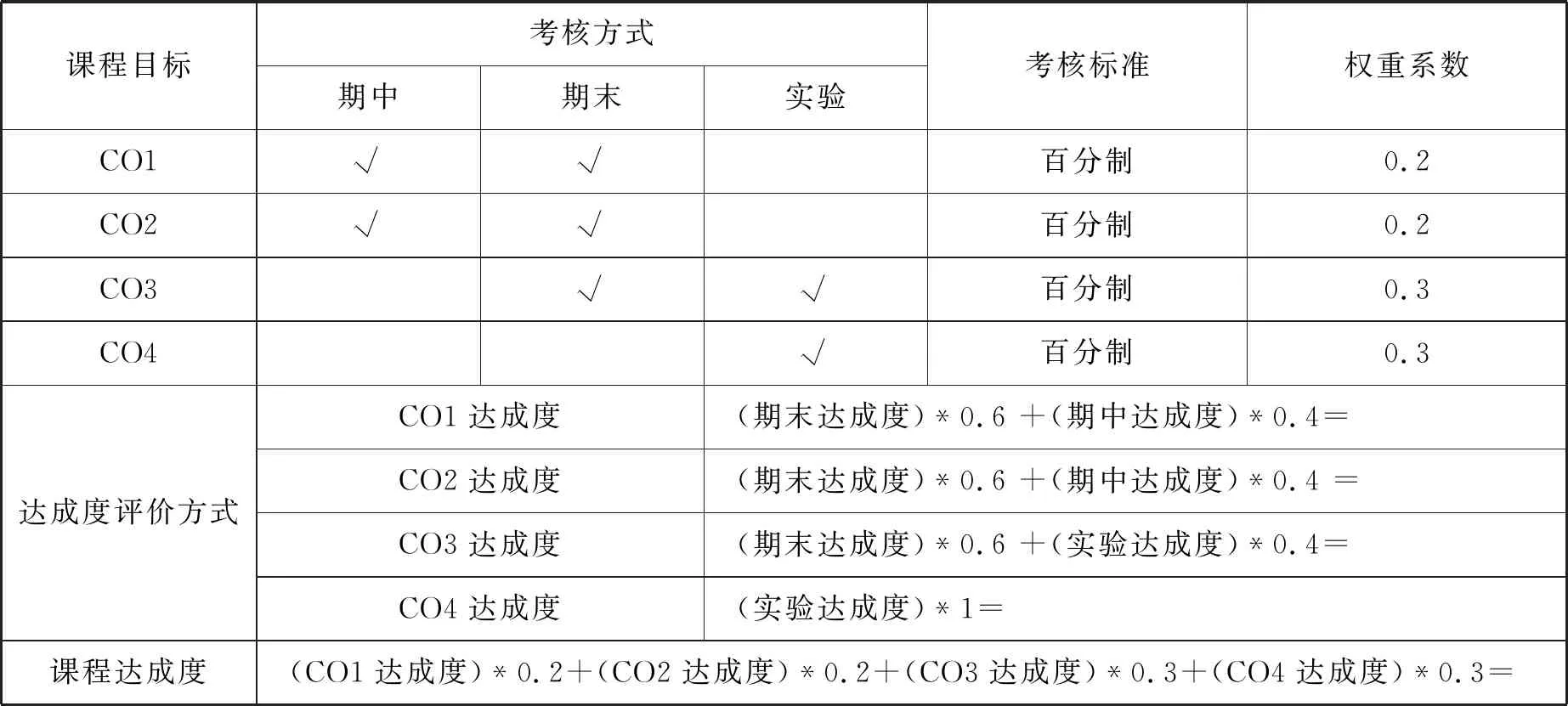
表1 《信息安全数学基础》课程达成度评价表
对毕业要求指标点达成度的评价,主要通过课程目标3和课程目标4来完成.如表2所示.
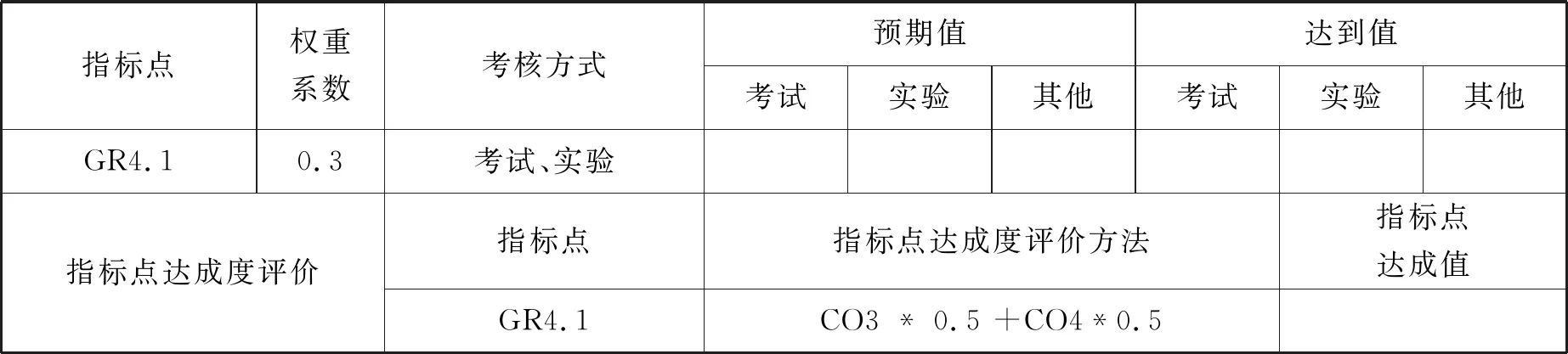
表2 《信息安全数学基础》课程毕业要求指标点达成度评价表
综合课程设计的评价与课程评价分开,独立评价.综合设计注重形成性评价,即综合考查学生在课题实施过程中各方面能力的体现,如文献综述、需求分析、算法设计与实现、报告撰写、现场答辩等,结合综合课程设计报告来对学生的能力和素质进行综合评价.综合课程设计I执行周期为15周,考核分为两个阶段三个部分,一是中期考核,综合课程设计执行10周左右,学生提交中期报告,由指导教师进行检查,了解学生的课题完成度和问题分析能力,并根据中期报告进行评价;二是期末答辩,在学期期末,学生完成综合课程设计并撰写课程设计报告,学院组织专家对综合课程设计进行答辩评审,主要考察课题的完成情况和学生的总结报告撰写情况.期末答辩前,指导教师还将根据每周讨论情况给出学生的平时成绩,并对设计报告进行评价,将平时成绩、中期考核成绩和报告评价成绩提交给专家组,由专家组结合答辩成绩进行统分,给出最终的考核成绩.考核成绩中,平时成绩占20%,中期考核占20%,期末答辩占30%,总结报告占30%.
3 教学实践
本课程自2019年开始实施以算法为核心的教学改革实践.与2018年相比,课程考核加大了实验环节所占考核比重,在平时成绩中从25%提升到了50%.从表3中可以看出,CO3和CO4的达成度显著提高,这也说明学生的实践能力得到了提升.
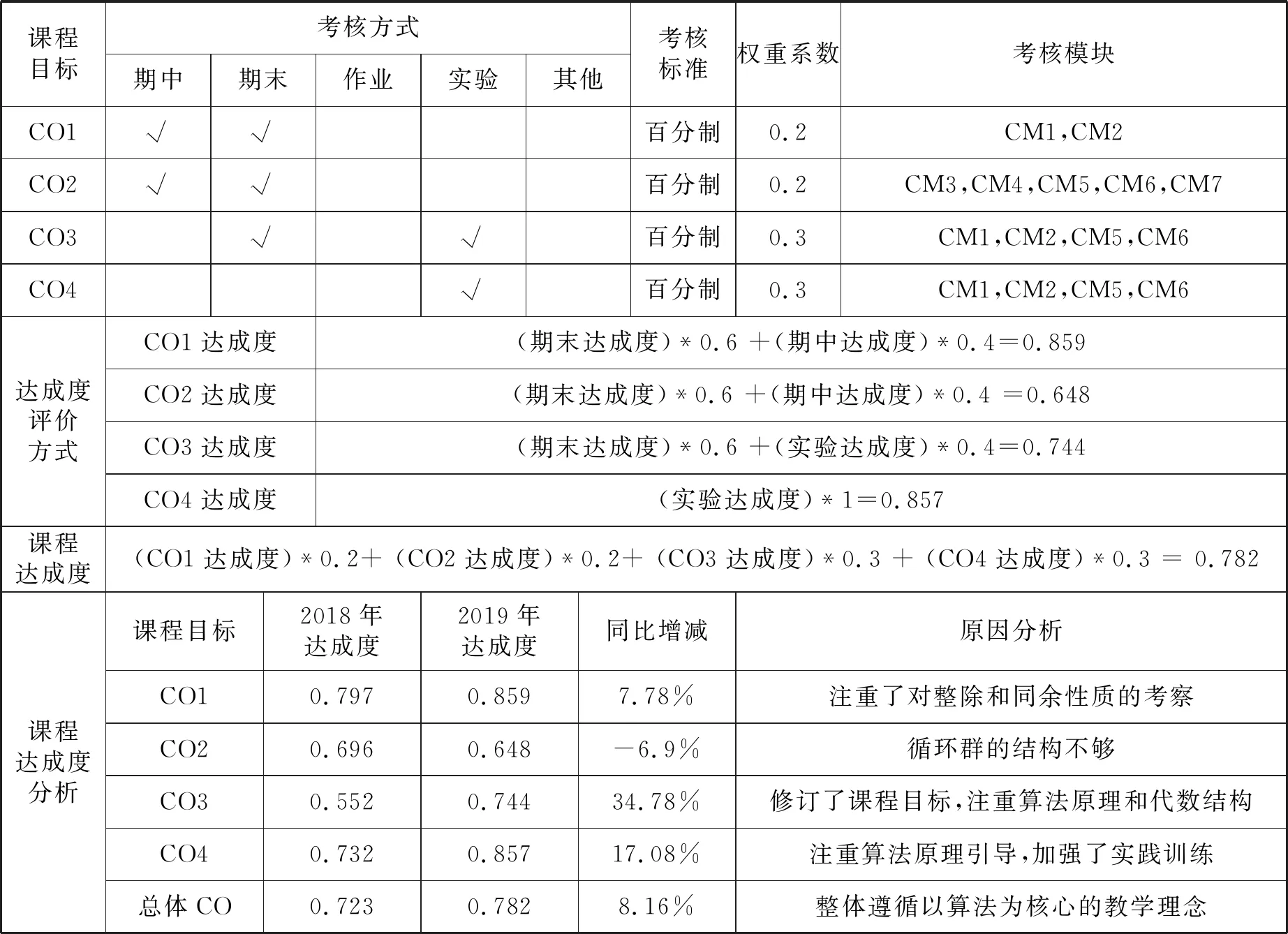
表3 2019年课程达成度评价及对比分析
毕业要求指标点达成度评价也从0.732提升到了0.801方面,如表4所示.
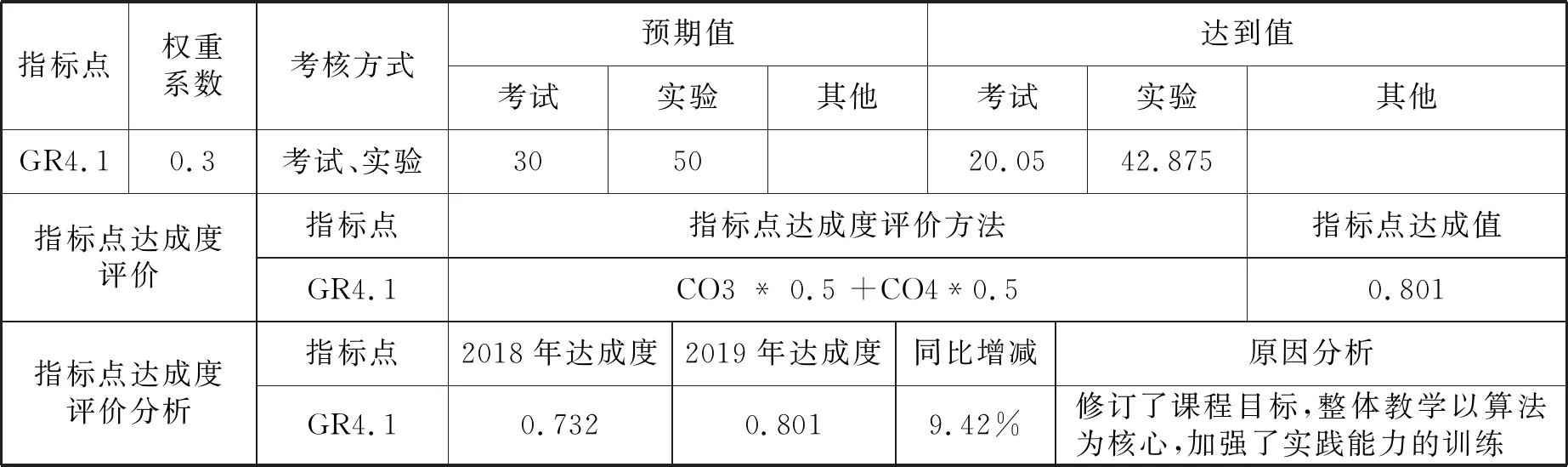
表4 2019年毕业要求指标点达成度评价及对比分析
此外,从图5中可以看出,在经过教学改革后,70分以上占比从55%提升到了64%,一定程度上也反映了学生的学习兴趣有所提升.
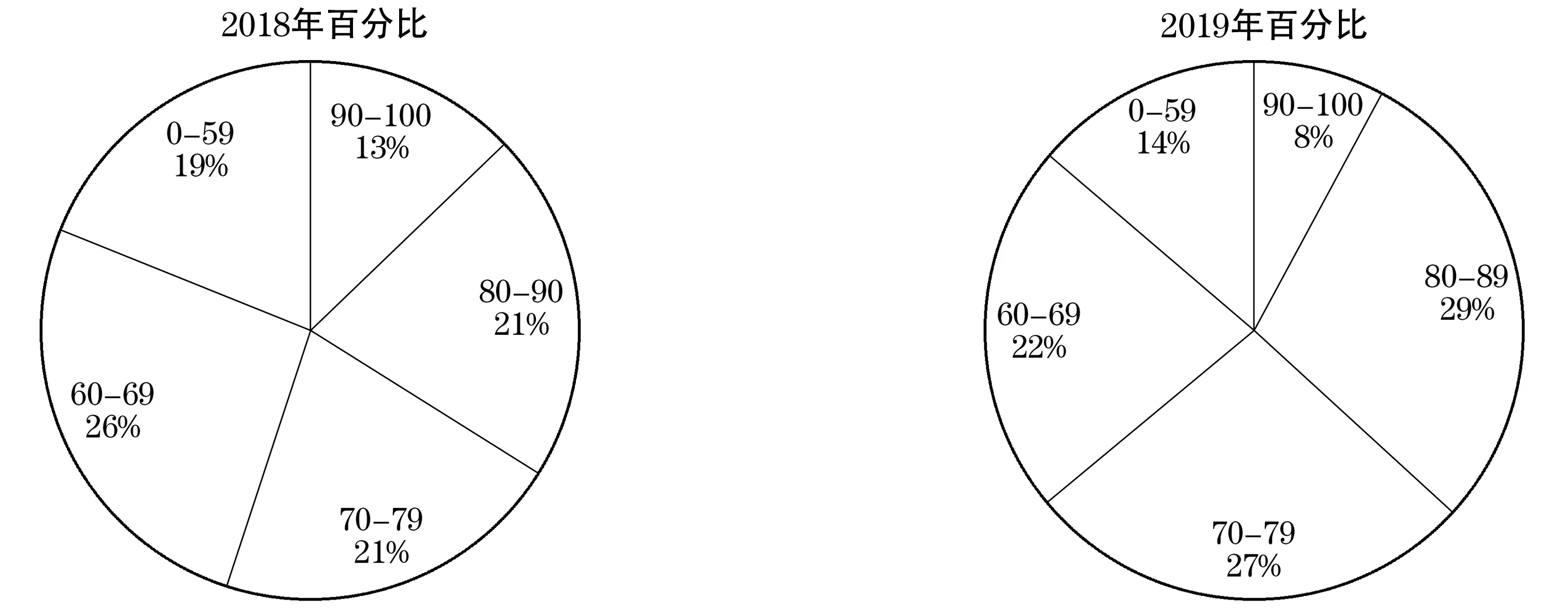
图5 信息安全数学基础2018年和2019年成绩分段统计对比
4 结 论
电子科技大学软件工程(互联网安全)专业信息安全数学基础自2019年开始实施以算法为核心的教学改革.教学改革符合工程教育认证理念,使课程教学从知识教学向能力培养转变.教学实践表明,提高了学生的学习兴趣和实践能力.未来,课程组将以全国高校密码数学挑战赛为载体[14],扩展课程设计内容,为学生参加此类竞赛打下坚实的基础.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

