将思政元素融入概率论与数理统计“金课”建设与实践
陈学慧, 李 娜, 赵鲁涛
(北京科技大学 数理学院,北京100083)
1 引 言
2017年中共中央、国务院印发的《关于加强和改进新形势下高校思想政治工作的意见》提出,把思想价值引领贯穿教育教学全过程和各环节,要坚持全员、全过程、全方位育人.“课程思政”即把思想政治教育融入各类课程教学中,实现三全育人格局的一种先进教育理念[1-2].近几年,高校德育教育理念发生了重大转变,以德育元素融入课程专业建设的教学研究成为关注热点[3-5].课堂教学是育人时代人才素养培养的主渠道.大学生的品格培养、正确价值观的塑造以及人格品质的养成,仅仅依靠高校专门化的思想政治理论课显然是不够的.事实上,各门课程均具有育人的功能,基于各门课程的价值属性,发挥高校各课程之间的协同作用,围绕培育核心人才的总体目标形成系统合力是课程思政建设的重要任务.这就要求,各类课程都要守好一段渠、种好责任田,与思想政治理论课同向同行,形成协同效应.
概率论与数理统计课程是大学数学三大基础必修课之一,受众面广,关注度高.通过本门课程的学习,学生初步掌握处理随机现象的基本思想和方法、运用概率论与数理统计的方法去分析和解决有关实际问题的能力,并为今后各学科领域进行理论研究和实践工作打下基础.北京科技大学概率统计教学团队积极开展概率论与数理统计“金课”建设研究与实践,至今已收获以下成果:一是线上课程资源建设方面.将两届全国青教赛一等奖的素材融入课堂教学,开发制作高质量线上慕课,2020年被评为首批国家级线上一流课程.二是线下课程教学改革方面.“以教学质量提升为核心的教学模式改革与创新——概率论与数理统计课程实践探索” 项目曾获北京市高等教育教学成果奖二等奖.三是教材建设方面.概率统计教学团队已出版《概率论与数理统计》《概率论与数理统计全程指导》《概率论与数理统计教学设计》《数学实验—概率论与数理统计分册》系列教材,受到老师和同学们的好评.
课程思政是“课程”和“思政”的有机融合,课程思政建设已成为各高校打造“金课”过程中关注的热点和难点问题.目前,中国知网上以“概率论与数理统计+课程思政”为主题查阅到的文献共10余篇,这些文献分别从教学内容[6]、教学方法[7]、实施路径[8]等方面阐述了课程思政教学改革与实践.但总体看来,教学案例思政元素的挖掘还不够充分,不少思政元素重复出现创新性不够;思政元素与专业知识融合度不高,难度不够,使得学生学习的挑战度不够.自2018年起,笔者“课程思政”示范教学团队自主开发设计教学案例,以“两性一度”的金课标准逐步建立起高质量的思政案例库.以不断更新和完善的思政案例参加各类教学比赛,至今已获得全国高校青年教师教学竞赛理科组一等奖两项,全国高校数学微课程教学设计竞赛全国一等奖一项,全国高校数学微课程教学设计竞赛华北赛区一等奖四项.同时,通过这些教学比赛及线上一流课程的建设,把课程思政案例进行推广宣传,已应用到中国农业大学、南京审计大学、哈尔滨理工大学、华南农业大学等10余所高校的概率论与数理统计课程教学中,为高校课程思政建设提供素材和思路.
2 课程思政教学研究与实践
2.1 典型线上思政案例设计 激发学生爱国热情
为落实立德树人根本任务,促进信息技术与教育教学实践深度融合,加快推进教育信息化转段升级,构建“互联网+教育”新生态,线上教学已成为思政课程教学模式中非常重要的环节.在线上慕课教学融合课程思政,选择典型的育人案例潜移默化地影响学生,对学生进行爱国主义教育,打造全方位育人.下面以概率论部分独立性知识点案例讲解为例.
2.1.1 独立性应用案例——近防炮导弹拦截问题
“万发炮”可以在一分钟内发射11000发的炮弹对导弹进行拦截.假设每发炮弹的命中概率均为0.004,且每发炮弹能否命中目标互不影响.问:为确保以0.99的概率击中导弹,至少要发射多少发炮弹?
解设事件A—导弹被击中;事件Ai—第i发炮弹击中导弹,i=1,2,3,…,n.有
A=A1UA2U…UAn,
A1,A2,…,An相互独立;p=P(Ai)=0.004,i=1,2,3,…,n.要使
P(A)=1-(1-p)n=1-(1-0.004)n≥0.99,
解得n≈1149,即至少需要1149发炮弹.
2.1.2 将德育元素融入教学内容
从例题的计算结果可以看出,在相互独立的条件下,命中率0.004的小概率事件重复进行1149次,事件“导弹被击中”至少有一次发生的概率可以达到99%.由此可以推断出,一个事件的发生概率很小,小概率事件在一次实验中几乎不可能发生,但是在无穷多次实验下,小概率事件一定会发生,这就是“小概率事件推断原理”,体现了唯物主义偶然性与必然性的辩证关系.借此原理告诫同学们,在现实生活中要趋利避害,科学的选择好的小概率事件,提醒同学们“勿以恶小而为之,勿以善小而不为”,及时纠正或避开不好的小概率事件,让不确定的小概率事件可掌握.
2.1.3 弘扬爱国主义精神,激发学生的爱国热情
通过课件图片(如图1)或小视频,让学生们了解当前世界主流的近防炮,包括美国的火神、俄罗斯的卡什坦和我国自主研发的万发炮.2019年10月1日,天安门广场举行了庆祝中华人民共和国成立70周年阅兵式.阅兵式中展示了威武霸气的万发炮1130,其射速每分钟1.1万发,目前装备在辽宁号、太原舰等航母和巡航舰上,可用雷达控制自动向来袭的导弹射击,能够有效拦截高超音速的导弹,拦截率达到96%,是当今世界上最先进的近防炮,我们可以骄傲的说“万发舰炮,中国最强”,在讲解中增强学生的民族自豪感,激发他们的爱国热情.

图1 课件中的课程思政
2.2 关注社会时政热点 培养学生应用创新能力
2020年春节,一场突如其来的新型冠状病毒疫情,打乱了人们的生活节奏.在这场疫情中,我们感受到了党和国家的强大,在中国共产党的坚强正确领导下,疫情得到了有效地控制.党中央、国务院高度重视新冠病毒核酸检测工作,中央应对新型冠状病毒感染肺炎疫情工作领导小组会议作出部署,要求着力提升检测能力,尽力扩大检测范围.新冠病毒核酸检测的有序推进,是有效防控新冠肺炎疫情蔓延的关键.核酸检测方法采用分组样本法,大大降低了检测次数和试剂盒使用量,那么,分组核酸检测的原理是什么?下面以概率论部分数学期望知识点进行分析.
2.2.1 数学期望的应用——分组检测问题
某高校共有2000人参加核酸检测,已知每人检测呈阳性的概率是0.001,现在采用两种方案进行采样化验:方案一: 逐一进行化验;方案二:每5人为一组进行分组化验,如果检验阴性则一次通过,如果呈阳性,再逐一检验;问哪一种方案最优?
2.2.2 逐一检测与分组检测对比结果
第一方案比较简单,逐一化验,所以化验次数为2000次.第二种方案因为检验次数不定,所以设随机变量X为一组检验所需的检验次数,根据第二种方案的操作过程,那么X的可能取值要么为1(全阴性),要么为6(阳性逐一化验),其概率值分别为X=1意味着5人全阴性,一个人血液阴性的概率为0.999,5个人血液阴性的概率为0.999的5次方,X=6意味着至少有一个阳性,也就是全为阴性的逆事件,则其概率为1-0.9995,那么每组需要的平均检验次数为
E(X)=1×0.9995+5×(1-0.9995)≈1.02.
设方案二总检验次数Z=X1+X2+…+Xn,Xi与X同分布.
E(Z)=E(X1+X2+…+Xn)=400×1.02=408≪2000.
因此,方案二远比方案一更高效.
2.2.3 联系时政,激发学生探究新知识的热情
分组检验问题的研究历史悠久,早在19世纪40年代第二次世界大战期间,美国征召了大量新兵入伍,相关部门希望对每个新兵做血液检测,以分析士兵是否感染梅毒.由于血液检测成本昂贵,对每个士兵都检测效率很低.统计学家Robert Dorfman设计了分组检验方法,这种方法是否能够降低检验次数取决于新兵感染梅毒的概率.如果概率较低可以大大提高检测效率,如果概率较高反而增加检验次数.为了进一步分析分组检验的检测效率,将问题推广到更一般情况,假设检验总人数N人,每人核酸检验阳性的概率为p,每m人一组,可以计算平均检验次数的表达式,或者讨论如何分组才能使检验效果最优等等,这些问题由同学自行查阅资料推导并讨论.
2.3 结合教学内容,培养学生理性思辨、明辨是非的能力
概率论与数理统计课程中的许多概念、公式、原理既是教学设计的基本内容,本身又渗透着辩证唯物主义的思想,是非常好的育人素材.数理统计部分的极大似然估计法、矩估计法、区间估计和假设检验都是重要的统计推断方法,都是通过样本的信息去推断总体的某一方面特征,由于样本的随机性,所得结论不能够保证百分之百正确.以课程思政教学目标为导向,结合概率论与数理统计的知识点,形成系统的教学案例,培养学生辩证的思维方式和面对科学问题的批判精神,提高大学生的应用创新能力.下面以假设检验知识点分析为例:
2.3.1 正态总体均值的假设检验——袋装机检验问题
某制糖厂厂家声称,厂里生产的袋装糖重量不低于0.5公斤,某天计量检验人员随机抽取9袋糖,算得平均重量0.489公斤,样本标准差为0.0152公斤.试求在显著性水平0.05下,确定厂家的声明是否可信?
2.3.2 求解过程
(i) 提出假设H0:μ=μ0=0.5,H1:μ<μ0;
(iii)H0的拒绝域C:T<-t0.05(8)=-1.8595;
2.3.3 检验结果分析
上述问题是在显著性水平α=0.05下做出的判断,对于事先给定的α,根据取样结果判断厂家的声明是否可信.若取样结果落入拒绝域,则认为厂家声明不可信;若取样结果未落入拒绝域,则暂且相信厂家声明.由此可见,检验结果与α的取值密切相关,改变α的值,可能会得到不同的检验结论.可以计算,当显著性水平α=0.025时,检验结果是暂且相信厂家的声明.因此,显著性水平α应根据研究属性和我们对结论准确性所持的要求而定.
2.3.4 培养学生的理性思辨能力
随着科学技术迅猛发展和知识经济迅速兴起,大学生具备理性思辨意识尤为重要,培养具有思辨能力的核心人才是当前教育的重要任务.在假设检验过程中,事先给定的显著性水平下,按照假设检验的求解步骤便可得出检验结论.那么,检验的推断结果一定是百分之百正确的吗?众所周知,由于样本的随机性,以样本结果进行假设检验而作出推断时,并不能地确定百分之百不发生错误.假设检验可能有两类错误:如果原假设H0是正确的,但通过试验结果的检验后却否定了它,这就是造成所谓第一类错误(弃真错误);反之,如果原假设H0是错误的,而通过试验结果的检验后却接受了它,这就是造成所谓第二类错误.简言之,假设检验的推断结果也可能是错误的.事实上,世间万物皆如此,绝对正确或绝对错误的事是很少的.在信息爆炸的时代,同学们遇到问题要进行合理的分析判断,提高思辨的能力才不会轻易被他人的言论遮蔽,进而有目的地选择正确信息、理性地解决问题.
3 教学效果评价
“关心学生的成长,对学生进行正确的价值观引导”是北京科技大学教学评价的一项重要指标.任课教师在传授专业知识的同时,典型的思政案例的设计有效的激发学生的学习兴趣,培养了学生理性思辨、明辨是非的能力,引导学生树立正确的价值观.反过来,课堂上同学们的阵阵掌声代表了他们对教师的认可和鼓励,督促着任课教师坚持不懈地进行课程思政教学改革和创新.
如图2、图3整理了“课程思政”示范教学团队近三个学期的学生线下课程评教结果,可以看出,“概率论与数理统计”的课程评价平均成绩达到98.07分,并且随着课程思政教学改革的不断深入,学生对教师的认可度有明显的提升.督导组及校内外专家在听课、查课、教改项目答辩等场合,也给予本课程高度评价,认为“‘概率论与数理统计’课程的讲台整体实力很强,讲课清晰,重难点突出,对课堂教学有设计.2020年3月,杨仁树校长听查课时给出如下评价:“授课中,将参加阅兵的士兵身高与数学教学内容中期望值、均方差等相结合,给人印象深刻,有利于更好地理解教学内容中的基本概念,此外,也体现课程思政的教学要求.
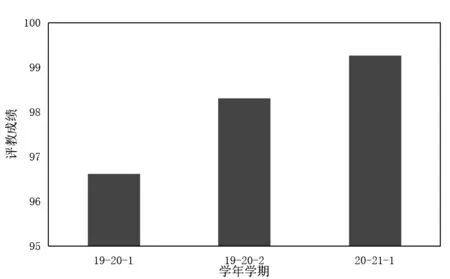
图2 概率论与数理统计评教成绩图

图3 线下课堂学生部分评语
“中国大学MOOC”的线上学习者对课程评价达到4.6分(满分5分),表明非常认同主讲教师的讲课方式.从线上学生评价来看,借助于鲜活的思政案例,加深了学生对基本概念的理解,增长了知识,开阔了眼界,感受到了概率统计的魅力,增强了应用概率统计知识去解释、解决实际生活中的随机现象的能力,也体现了课程思政建设的育人成效.
4 结 论
全面开展课程思政教育,是新时代高校提高人才培养质量的重要举措.本文主要阐述了概率论与数理统计“金课”建设实践与课程思政教学改革融合过程,从教学模式、教学案例、教学评价等方面探索“课程思政”教学改革的新思路.做好“课程思政”工作,关键要提高高校教师育德意识,挖掘好的素材,深化大数数学课程思政教学改革,将课程思政元素紧扣课程知识内容.在学习专业知识的同时,引导学生树立正确的世界观、人生观、价值观,培养学生的爱国主义情怀和创新性思维,以实现“润物无声”的育人功效,为社会主义教育强国的铸就贡献力量.
致谢作者非常感谢审稿专家提出的宝贵意见以及参考文献对本文工作的启发.

