“正弦函数、余弦函数的图象”教学设计

浙江省杭州第十四中学(310006) 何波禄

1 教学问题诊断与设计思路

正弦函数、余弦函数的图象是《普通高中课程标准实验教科书数学A 版必修第一册》第五章第四节课的内容.

学生通过前面的学习,对用描点法研究函数图象并不陌生,但由于正弦函数与余弦函数自身的特殊性,在作图环节可能会遇到如下问题:

(1)对于借助三角函数线描点感到“突兀”;

(2)“五点法”作图时,难以想象为什么要取五个关键点,为什么不用这样子的点;

(3)作余弦函数图象时,不易联系诱导公式根据图象变换得到图象.

基于以上分析,本节课的教学重点为绘制正弦函数、余弦函数的图象和五点法作图;教学难点为如何利用单位圆中的正弦线作正弦函数图象.

教学设计遵循从局部到整体,从特殊到一般的原则,以问题驱动教学,问题设置层层深入,引导学生思考“利用单位圆中的正弦线描任意点(x0,sinx0)”,从而攻克“利用单位圆中的正弦线作y= sinx,x ∈[0,2π]的图象”这个难点;再让学生模仿作函数y=sinx,x ∈R 的图象,展示有问题的学生作图,启发学生“找出体现图象形状特征的五个关键点”;通过直接给出诱导公式六,提示学生直接从正弦曲线平移得到余弦曲线.运用多媒体及数学软件等辅助教学手段可以极大地激发学生的学习兴趣,用观察、启发、探究相结合的方式组织教学.

2 教学过程

2.1 温故知新,导入新课

回顾正弦函数、余弦函数的概念,对于一个新的函数,我们通常借助函数图象研究函数性质,本节课我们就一起作出正弦函数和余弦函数的图象.

【设计意图】引导学生用研究函数的基本思路研究三角函数.

2.2 正弦函数图象

问题1: 我们最常用的作图方法是什么?

问题2: 用描点法作正弦函数图象时,如何在直角坐标系中作出点

4.若学生回答可以取一些特殊点, 追问你打算取哪些点? (并作图寻找问题,说明取的点不足以反映出函数图象的特征)

问题3: 对于任意实数x0,如何作出点T(x0,sinx0)?

预设追问: 1.正弦值是如何定义的?

2.你能用一条线段表示正弦值吗?

对于任意实数x0(教师在直角坐标系的x轴上标出点x0,见图1),用单位圆中的正弦线刻画sinx0的大小,教师板演描点T(x0,sinx0)的完整过程,并与学生一起总结如下步骤:

第一步,新建直角坐标系并作单位圆,记单位圆与x轴的交点为点B;

第二步,作角,我们可以通过如下方式实现: 从点B开始逆时针取弧长所对应的圆心角即为x0;

第三步,作正弦线,过点P作x轴的垂线,交x轴于点M,则MP即为正弦线,MP=sinx0;

第四步,用尺子测量MP的长度;

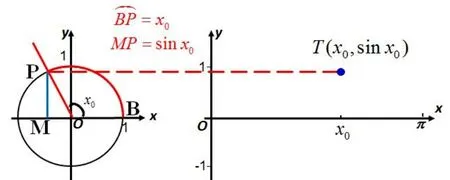
图1

第五步,描点,在直角坐标系中描出横坐标为x0,纵坐标为MP的点T(x0,sinx0).

我们可以将上述描点方法再简化些,若把两个直角坐标系的x轴放置在同一水平线上,只要平移点即可.

在单位圆中取弧长x0, 可以通过如下方式实现: 假设|OC|=x0,令点O与单位圆上的点B重合,让圆滚动起来,使得点P与点C重合时,停止圆的滚动,那么由圆的运动轨迹知教师可以用几何画板作演示,见图2.

图2

【设计意图】利用正弦线描点是本节课的难点,教师通过不断追问的方式从特殊到一般,小步前进攻克难点,并且利用PPT,几何画板等教学辅助手段给予演示,生动形象,吸引学生观察、思考、分析,对描点步骤进行归纳总结,促进学生知识体系的建构和数学思想方法的形成.

掌握了利用正弦线描点的方法, 就可以画正弦函数在[0,2π]的图象,教师几何画板演示作图: 把x轴上从0 到2π这一段分成12 等份,使x0的值分别为它们所对应的角的终边与单位圆的交点将圆周12 等分,再按上述画点T(x0,sinx0)的方法,就可以平移得到自变量取这些值时对应的函数图象上的点,最后用光滑的曲线连接起来就得到了函数y=sinx,x ∈[0,2π]的图象(图3).

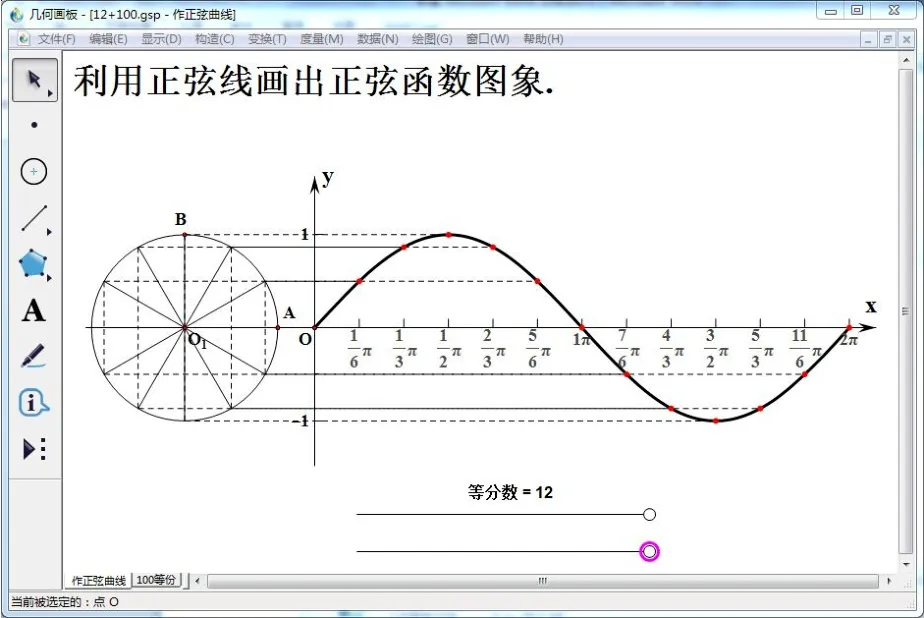
图3

我们知道在区间[0,2π] 上取的点越多, 画出越多的点T(x0,sinx0),得到的函数图象越精确,尝试将其100 等分(图4),1000 等分(图5)并观察.显然点越多,图象越精确,将区间[0,2π]1000 等分得到的描点图,点很密集,看上去几乎是一条连续的曲线.

【设计意图】通过几何画板呈现出用平移正弦线的方法绘制函数y=sinx,x ∈[0,2π]图象的过程,并展示对单位圆进行100 等分,1000 等分后对应的描点图,生动形象,吸引学生眼球,让学生加深印象.

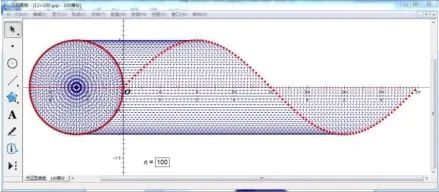
图4

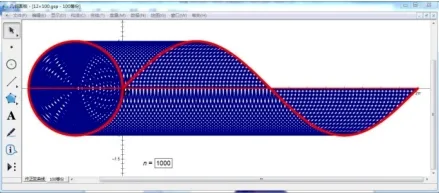
图5

回到12 等分的几何画板课件, 直接用几何画板作出y= sinx的图象,它与用单位圆中的正弦线作的图在[0,2π]上是重合的,其余部分有“周而复始”的特征,引导学生回答若不借助作图软件,你能作出完整的正弦函数图象吗?

问题4: 如何在直角坐标系中作出y=sinx,x ∈R 的剩余图象?

追问: 理论依据是什么?

因为终边相同的角有相同的三角函数值, 所以函数y=sinx,x ∈[2kπ,2(k+1)π),k ∈Z 且k /=0 的图象,与函数y=sinx,x ∈[0,2π)的图象的形状完全一致,只要将函数y=sinx,x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到y=sinx,x ∈R 的图象(图6),教师用PPT 展示平移过程,我们称正弦函数的图象为正弦曲线.

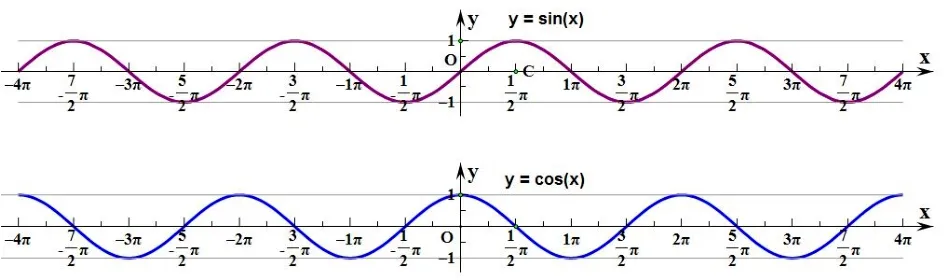
图6

【设计意图】教师对学生的猜想追问理论依据,对学生的回答进行补充说明,从“周而复始”的现象引发思考,再用诱导公式予以理论支持,利用PPT 课件演示平移过程,得到y=sinx,x ∈R 的图象.

2.3 五点法作图

下面请学生自己模仿图6 作正弦曲线,展示学生的作图(图7),观察图7,找出不规范的地方,比如最高点离平衡位置的距离与最低点离平衡位置的距离不一致,相邻两个零点间的距离也不一致,引导学生思考,抓住哪些点能帮助我们画出标准的图象.

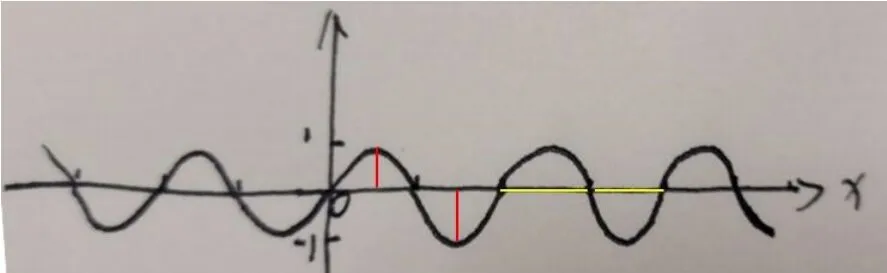
图7

问题5: 在作正弦函数y= sinx,x ∈[0,2π]图象时,应抓住哪些关键点?

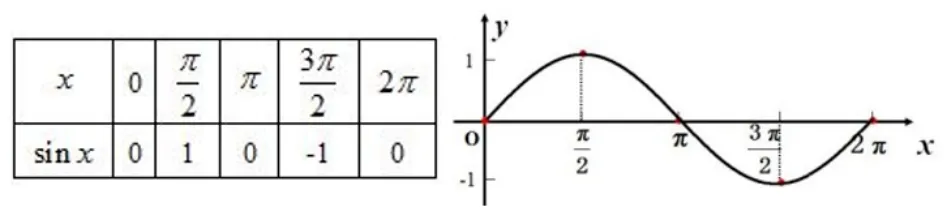
图8

【设计意图】首先让学生模仿作图,充分暴露学生存在的问题,引导学生关注最高点,最低点和平衡位置的点,提出利用五点法作简图的必要性与合理性,再总结归纳五点法作图的步骤,教师把五点法作图过程在黑板上进行详细板演.

2.4 余弦函数图象

【设计意图】通过问题形式,让学生从正弦函数与余弦函数解析式之间的关系联想得到这两个函数图象之间的关系,用PPT 课件演示平移的过程,明确应用图象变换作余弦曲线的方法.

追问1: 如果把图6 中上下两个直角坐标系都去掉,你能区分哪个是正弦曲线,哪个是余弦曲线吗?

追问2: 我们再把直角坐标系加上,这时你能区分哪个是正弦曲线,哪个是余弦曲线吗?

根据追问引导学生发现正弦曲线和余弦曲线的相同点:形状一样,不同点: 在直角坐标系中的位置不一样.

【设计意图】为研究正弦函数、余弦函数的性质做准备.

下面请你用“五点法”作出函数y=cosx,x ∈[0,2π]的简图.

【设计意图】类比作y=sinx,x ∈[0,2π]的简图,让学生学会用五点作图法作y= cosx,x ∈[0,2π]的简图,巩固五点法作图方法,培养学生的归纳能力和动手实践能力.

2.5 实践与应用

例1 画出下列函数的简图:

(1)y=1+sinx,x ∈[0,2π];

(2)y=−cosx,x ∈[0,2π].

学生采用的作图方式主要有两种: 五点法,图象变换法.用希沃授课助手展示学生的解答,请其他同学指出存在的问题并加以纠正,特别是曲线的凹凸性.

【设计意图】通过例题练习使学生明白作函数简图时常用“五点法”和“图象变换法”这两种方式.

2.6 归纳小结

先由学生反思学习内容并回答,教师再补充完善.

1.作正弦曲线、余弦曲线的图象,一般有几何作图法(三角函数线),描点法(五点法,最常用),图象变换法;

2.五点法作图的步骤是: 列表,描点,连线.

【设计意图】让学生小结本节课的主要知识, 养成学习——总结——学习的好习惯,培养学生总结归纳能力和语言表达能力.

3 教学反思

本节课以问题驱动方式进行教学,以6 大问题为主线贯穿课堂始末,以问题解决为教学线索,并在计算机辅助教学下,学生的思维由问题开始,由问题深化,逐步解锁教学重点,突破教学难点.

首先给出问题1 至问题3,引导学生思考“利用单位圆中的正弦线描任意点(x0,sinx0)”,从而攻克“利用单位圆中的正弦线作y= sinx,x ∈[0,2π]的图象”这个难点,之后用几何画板演示正弦函数的几何作图法,生动形象,吸引学生眼球,让学生加深印象.接着设置问题4,引导学生回答出关键词“平移”,得到正弦曲线.再让学生模仿作图,启发学生“找出体现图象形状特征的关键点”,引出“五点法作图”.设置问题6,引导学生利用正弦曲线作出余弦曲线.最后通过练习加以巩固.