常量替换再探究——一节研究性学习课的教学实录与反思

广东省广州市番禺中学(511400) 黄 殷

《数学通报》2011 年第10 期第30 页刊登了李爱生老师的《常数替换 精彩迭现》[1]一文,笔者读后受益匪浅.该文从一道例题出发,利用“常量替换法”探究出圆锥曲线的多个结论.笔者认为该文章里的一些定理,还值得作进一步的探究推广,于是挑选了其中的定理7、8、9,在学校高二数学研究性学习课堂里,进行了探究教学,取得了不错的效果.以下是本节课的课堂实录与反思.

1 原问题呈现

定理7P(s,t)是椭圆=1(a ＞0,b ＞0)上一点,直线l与该椭圆相交于A、B两点,且PA⊥PB,则直线l过定点

定理8P(s,t)是双曲线=1(a ＞0,b ＞0,a/=b)上一点,直线l与该双曲线相交于A、B两点,且PA⊥PB,则直线l过定点

定理9P(s,t)是抛物线y2=2px(p/=0)上一点,直线l与该抛物线相交于A、B两点,且PA⊥PB,则直线l过定点(s+2p,−t).

对于定理8,笔者在黑板上展示了李老师给出的证明过程:

设A(x1,y1),B(x2,y2), 直 线l:y=kx+m, 即双曲线即

又因P(s,t) 在双曲线上, 故有= 1, 即b2s2−a2t2=a2b2, 所 以①可化为b2(x −s)2−a2(y −t)2+2[b2(x −s)s −a2(y −t)t]·1=0,即

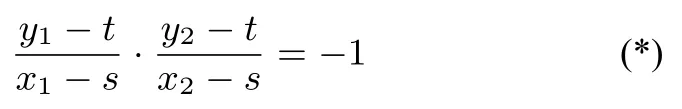
得:=−1, 即m=故直线l的方程为该直线经过定点当直线的斜率不存在时,验算可知,结论仍成立.

2 教师引导探究

在展示了以上证明过程后,笔者提出了以下问题,引导学生进行探究.

欣赏了刚才的推导过程, 学生听到老师所提的问题后,均跃跃欲试,在做一番推导和讨论交流后,有一位学生举起了手,我让他上台板书.

师: 很好! 参考刚才这位同学推导的结论,我们是不是可得到以下精彩的结论呢?

结论1P(s,t) 是双曲线= 1(a ＞0,b ＞0) 上 一 点, 直线l与 该 双 曲线相交 于A、B两 点, 且kP A · kP B=n,n为常数且n /=则直线l过定点

学生纷纷点头表示认同.看着自己推导出来的结论,学生的成功感油然而生!

师: 结论1 其实是定理8 的一般形式.对于定理7,我们能不能也得出它的一般形式呢?

学生异口同声地回答: 能!

师: 怎样得到呢?

师: 不错! 这是一种常规的思路,但过程会繁琐一些.大家再想想,有没有其他的方法呢?

生3: 其实只要把双曲线方程中的“−b2”改为“b2”, 就变成椭圆的方程了.那我觉得把结论1 中所有的“−b2”改为“b2”就行了.

生3 话音刚落,课室里发出了一阵讨论声,不少学生都在点头,并向生3 投去敬佩的眼光.

师: 很好! 看来生3 这位同学确实是动了脑筋思考的.不错, 刚才我们用“=n”替换了(*) 式的=−1”,得到了一个精彩的结论,现如果用“−b2”替换结论1 中的“b2”,我们同样可以得到另一个精彩的结论.

结论2P(s,t) 是椭圆= 1(a ＞0,b ＞0)上一点, 直线l与该椭圆相交于A、B两点, 且kP A ·kP B=n,n为常数且n /=则直线l过定点

这时,笔者明显感觉到课室的“温度”上升了,有在讨论推导过程的, 也有在啧啧赞叹的, 还听到有学生讨论定理9的一般形式.

师: 大家再想一想,能否进一步得出定理9 的一般形式呢?

几个学生不约而同地说: 可以用“kP A ·kP B=n”代替定理9 中的“PA⊥PB”.

师: 非常好! 看来同学们已经感受到“替代”的威力了.下面给大家一点时间推导,然后请一位同学上台来为大家板演.

生4: 证明: 设A(x1,y1),B(x2,y2),直线l:y=kx+m,即抛物线y2=2px可变为抛物线

又因P(s,t) 在抛物线y2= 2px上, 故有t2= 2ps, 所以②可 化 为(y −t)2+ 2[t(y −t)−p(x −s)]·1 = 0, 即(y −t)2+2[t(y −t)−p(x −s)]·整理,得因 为kP A · kP B=n, 所 以=n, 则=n,解得m=

故直线l的方程为y=−t,该直线经过定点当直线的斜率不存在时,验算可知,结论仍成立.

师: 通过推导探究,我们不难发现,通过“替代”,在抛物线中也可以得到精彩的结论.

结论3P(s,t)是抛物线y2=2px(p/=0)上一点,直线l与该抛物线相交于A、B两点,且kP A·kP B=n,n为常数且n/=0,则直线l过定点

3 层层推进,拓展探究

话音刚落,课室中开始“骚动”起来,讨论声、争辩声时起彼伏.

师(微笑,投去肯定的眼光): 你们可以大胆地试一试.

这两位同学分别就双曲线与椭圆、抛物线进行探究并上台板书.

师: 根据同学们的推导,我们可得到以下一组更精彩的结论:

结论4P(s,t)是双曲线上一点,直线l与该双曲线相交于A、B两点,且kP A+kP B=n,n为常数且n/=0,则直线l过定点

结论5P(s,t)是椭圆=1(a ＞0,b ＞0)上一点,直线l与该椭圆相交于A、B两点,且kP A+kP B=n,n为常数且n/=0,则直线l过定点

结论6P(s,t)是抛物线y2= 2px上一点,直线l与该抛物线相交于A、B两点, 且kP A+kP B=n,n为常数且n/=0,则直线l过定点

至此,学生们都雀跃地沉浸在自己探究所得的这些结论中.

师: 从一个问题出发,结合其产生的背景,通过探究推理,展望其未来的发展,这过程虽艰辛,但却是快乐的! 只要我们抱着一颗不断探索、不断追求的恒心,其收获一定是丰富而精彩的!

4 课后反思

4.1 关于数学研究性学习

数学研究性学习是一种实践性较强的教育教学活动,学生应通过自己亲身参与的探究活动来获取知识、得出结论,而不是由教师将现成的知识、结论通过传递式教学直接教给学生.数学研究性学习所探究的问题不一定是课本上的,亦可充分利用课外的资源.除此,教师还要了解学生已有知识,学生能达到“最近发展区”等.本节研究性学习课就是在学生学习完“圆锥曲线”这一章,掌握了椭圆、双曲线、抛物线的方程、图像和性质等问题后开展的.

4.2 教师主导地位与学生的主体地位

新课程标准强调教学过程中学生的主体地位,因此教师要发扬民主教学,要鼓励学生积极参与探究.更重要的是,教师应注意鼓励学生提出独立见解,还应认真聆听学生的提问,引导学生从不同角度思考和探究问题,使学生的思维和创造性在课堂中发光.如本节课中学生2 的证明方法虽然比较麻烦,但却是很多学生首先会想到的方法.教师此时就要发挥主导作用,一方面要给予充分的肯定,另一方面要引导学生思考其他的方法,唤醒学生的探究意识.

4.3 教师的设问是关键

本节课设置了一些列的启发性问题, 如:“...改为...”、“能不能得出它的一般形式”、“有没有其他的方法”这些问题都具有很大的发散性,从而激发了学生的求知欲望和创新热情.学生通过参与探究过程,培养了自身的发散思维能力和创造性、开拓性思维品质.学生也能很好地感受到由探究所得带来的成功感和喜悦感.