几何画板在初中数学课堂教学的运用策略

安徽省濉溪县教育科学研究室(235100) 杨经验

几何画板能够动态地展现出几何对象的位置关系、运动变化规律,有着传统尺规作图所无法比拟的优越性,其严谨的作图程序、强大的作图和计算功能,能有效地提升学生数学的水平和能力.在数学教学设计及课堂教学中,使用几何画板,可以使教学更加形象化、生动化、多样化和趣味化,这更有利于揭示数学概念的形成过程,呈现数学知识的发生过程,展示数学思维的形成过程;有利于培养学生数学图形构建能力及空间想象的能力[1].经过不断地学习探索实践,在数学教学中运用几何画板已取得显著成效.在农村初中数学教学设计及其课堂实施中如何运用几何画板呢? 下面几条是具体做法.

1 利用几何画板创设问题情境,激发学生学习兴趣

数学是从问题开始的,每一节数学课都离不开问题.这些问题是由教师一道一道的讲解,还是由学生自己探究呢?时代优势教学理论特别强调学生自己探究的重要性.在学生自主探究中,几何画板可以通过创设合适问题情境,给学生自主探究提供帮助.例如, 在讲解函数的最值问题时, 可以用几何画板提出这样的问题: 在圆的内接矩形中,边长比是多少的矩形面积最大? (请用画板软件探索结果).学生们可以很快就投入到操作和实践中,通过移动圆上的动点,比较边长的关系,便可以很快得出结论: 圆的内接正方形即边长比为1 的矩形面积最大.教师接着再问,为什么圆的内接正方形是圆的内接矩形中面积最大的呢? 学生们你一言,我一语互相讨论起来,进而在教师的引导下,利用二次函数求最值的方法,得出了证明……学生在课上,经历了探索——猜想——证明这三个数学学习的必须阶段,使知识得到了进一步的内化,大大提高了农村孩子的学习效率.

初中数学枯燥又抽象,不少的学生对数学敬而远之,甚至是惧怕和厌恶,特别是在初中接触了几何与函数之后,这种情绪更为强烈,这极大地压抑了学生的学习潜力.几何画板具有强大的动态变化功能,一流的交互功能,能以浓缩的形态给学生提供数学背景,通过学生的参与和亲手操作,枯燥抽象的内容变成生动形象的图形,原本不明白或不甚明白的概念等变得一目了然[2].以往用圆规、三角板绘制几何体,是不动的一个图形,几何画板运用动态的几何图形培养了学生空间想象的能力.

当我们使用几何画板动态地、探索式地表现直线与圆的位置关系,还有像圆锥的侧面展开图等等,都能形象化地直观呈现.原本静止枯燥的数学课变成了生动、活泼、优美感人的舞台,学生情绪高涨,专注渴求和欣喜的神情挂在脸上,作为老师的我们感到无限欣慰.几何画板一时成了师生的热门话题,使学生深刻体会到:“自己的眼睛可以看到自己在现实生活中看不到的一面”、“数学原来也能这样来学”、“想不到数学还真有趣”……

兴趣是学生学习的最好的老师, 是学生学习的原动力.实践证明使用几何画板探索学习数学不仅不会成为学生的负担,相反变抽象为形象,给农村孩子的学习生活带来极大的乐趣,孩子们完全可以在轻松愉快的氛围中获得知识.

2 鼓励学生利用几何画板自主参与数学学习

当学生对数学产生了兴趣,老师可以鼓励学生,利用几何画板这一工具,自主参与数学研究[3].例如,证明“三角形中,如果有两个角的平分线相等,则这个三角形是等腰三角形”这一问题,由于该题目的证明思路很不容易被找到,学生尝试用多种方法思考证不出来时,提出了这样的问题:“老师,你让我们证明的题目是正确的吗? ”教师可以提示学生用几何画板对题目进行验证.学生作出了图形,并测量了有关的线段的长度,当通过拖动M、N两点,在找准使AM与BN相等的点时,学生得到AC与BC的值总是相等的.于是,在验证了结论是正确的这样一种良好心理的支撑下,学生兴奋地告诉说:“老师,题目的结论是正确的,我要再试试如何证明.”

几何画板不仅在学生解题时很有用处,而且对新知识的学习也很有用.如学习“三角形三内角和为180°”定理时,教师可以让学生绘制一个三角形,测量出每个角的度数求出三内角和的值,并拖动三角形的任一个顶点,观察三个内角之和是否仍保持为180°.在具体论证之前,学生利用几何画板,对问题由感性认知到理性认同,这为下一阶段的学习作了很好的铺垫.再如勾股定理、圆周角定理、切线长定理等重要数学定理的证明,利用这种方法都能起到很好的教学效果.

在八年级下册中的四边形一章中,很多学生很容易将常用的四边形性质混淆,如矩形、菱形、平行四边形、正方形等.对于中点四边形更是弄不明白,传统的教学方式中,教师就需要画很多的图形进行证明,这更容易令学生产生眼花缭乱的感觉.运用几何画板,我们可以将其进行整合与变形,可以让学生举一反三,快速掌握相关知识.例如,在一节习题讲评课上,教师设计了如下一组题目: 顺次连结四边形的各边中点所得到的图形是? 学生经过思考和证明不难得到结论,进而教师利用画板按钮变换图形和题目引出下列变式习题: 变式1: 顺次连结矩形的各边中点所得到的图形是? 变式2: 顺次连结菱形各边中点所得到的图形是? 变式3: 顺次连结正方形各边中点所得到的图形是? 变式4: 顺次连结对角线相等的四边形各边中点所得到的图形是? 变式5: 顺次连结对角线互相垂直的四边形各边中点所得到的图形是? 变式6:顺次连结对角线互相垂直且相等的四边形各边中点所得到的图形是? 学生利用几何画板,用动态的图促进学生深入思考,以便快速总结出规律.

3 利用几何画板提高课堂教学效率

3.1 利用几何画板动态展示教学内容

几何画板可以动态展示教学内容或数学问题,使教学更加直观、生动,这有利于激发学生的学习兴趣,增强教学的趣味性.数形结合思想是一个非常重要的数学思想.数学家华罗庚说:“数缺形时少直观,形缺数时难入微”.几何画板为“数形结合”创造了一条便捷的通道,它不仅对几何模型的绘制提供信息,同时,可以解决学生难以绘制的图形,而且提供了图形“变换”的动感,丰富多彩的“动画”模型,给农村学生一种耳目一新的视觉感受,使学生从画面中去寻求到问题解决的方法和依据,并从画面中去认清问题的本质,帮助学生更好地理解数学基本概念.

在引入几何画板之后,可以测量各种数值以及进行各种函数运算,在图形的变化过程中,数量变化特征也可以直观地展现在学生眼前,“以形助数”,“用数解形”,这在传统教学中是无法办到的.比如,在学习二次函数与一元二次方程的关系时,用几何画板画一个二次函数图像y=ax2+bx+c.各参数的变化情况以及数量关系都显示在同一屏幕上(如图1 二次函数图像的演变), 不用老师开口, 学生就会发现b2−4ac的值与抛物线与x轴的交点个数的变化规律,以及a、b、c的变化对二次函数的图像形状及位置的影响.这种做法非常形象直观,易于接受,比过去直接用理论来说明或简单地在黑板上画几个草图来讲解的效果会好得多.

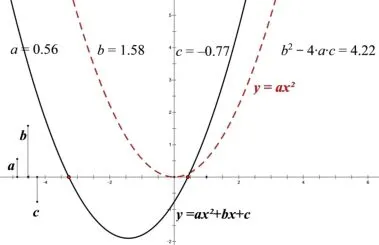
图1

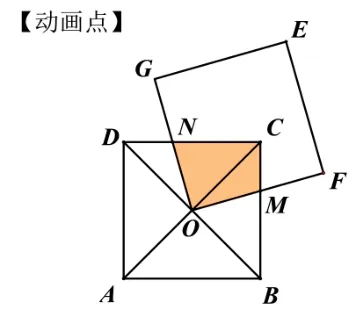
图2

在边长为a的正方形ABCD中,对角线AC、BD相交于点O,正方形OFEG与边BC,CD相交于点N、M,求四边形ONCM的面积(如图2).该问题解决关键在于得出四边形ONCM的面积与三角形OBC的面积相等,引导学生注意四边形OFEG的运动特征,让学生应用几何画板的动画特征,转动正方形OFEG,观察四边形ONCM面积的变化,从而探究出S四边形OMCN=SΔOBC的结论.

3.2 利用几何画板揭示问题本质

在解决数学问题中,由于问题本身的抽象性和推理的复杂性,学生花费了很多时间都未能把问题证明出来,此时,产生对问题的疑义并对问题真实性进行验证是一种极为可能并想去做的事.因为验证一方面可以缓解心理紧张和心理焦虑,变换思维角度,对问题进行再认识;另一方面可以调节心理平衡,重塑解题信心.学生在通过实验验证,可以确定问题的正确性.这将会增强学生解决问题的动力.从而帮助学生有效地克服推理过程中产生的心理障碍[4].例如,研究函数图像的性质,特别是增减性,是教学的难点,有了几何画板,就很容易解决这一问题.

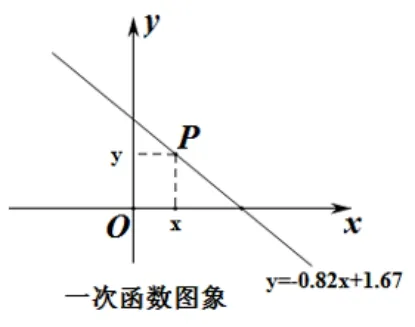
图3

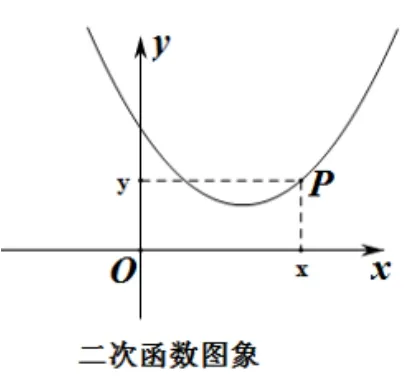
图4

(1)一次函数(如图3): 在坐标系内,任作一条直线,很容易得到它的解析式,我们拖动直线,就可以看到它的k和b在不断变化,学生们自己操作,仔细研究,就可以总结出,k、b大小与图像所经过的象限的关系.如下图,如果拖动直线上的点P,则它的横坐标和纵坐标都在同时变化,变化趋势明显.这样,当k ＞0 和k ＜0 时,极易掌握一次函数的增减性.(2)二次函数(如图4): 在研究二次函数图像的增减性时,我们拖动抛物线上点P,可以很形象地看到,y随着x的增大,一会儿增大,一会儿减小.问及同学们它的分界线在哪里,再次研究后都能回答是抛物线的对称轴.

3.3 利用几何画板进行数学实验

在教师的引导下, 几何画板可以给学生创造一个实际“操作”几何图形的环境,学生可以任意拖动图形、观察图形、猜测和验证结论,在观察、探索、发现的过程中增加对各种图形的感性认识,形成丰厚的几何经验背景从而更有助于学生对数学的学习和理解.同时几何画板还能为学生创造一个进行几何“实验”的环境,有助于发挥学生的主体性、积极性和创造性,充分体现了数学教学不仅要培养学生计算、演泽等具有根本意义的严格推理的能力,还培养学生尝试归纳、探索、寻找相似性等非形式推理能力的思想.

实验方法在数学科学中的作用愈来愈被重视,除了直接观察、假想试验,统计抽样等方法也日益被采用.而几何画板的使用,使学生进行数学实验多了一件有用的工具,使得在课堂上让每个学生进行数学实验成为可能.这种数学实验,对学生主体意识的形成,主动参与数学实践本领的提高,自行获取数学知识的能力培养,都将发挥作用.例如,(1)在计算机上用几何画板软件画任意一个三角形,再画出它的三条中线,有什么规律? (三角形三条中线交于一点)然后拖动三角形的顶点A随意改变所画的三角形的形状,看看这个规律是否改变.(2)在计算机上用几何画板软件画任意一个三角形,量出它的各内角并计算它们的和,然后拖动顶点改变所画三角形的形状,再量出变化后的各内角计算内角和.从而得出“三角形内角和等于180 度”这一结论.

4 使用几何画板的教学体会

几何画板作为一种新的认知工具,一定能得到广泛的使用.设想,如果学生能进一步掌握操作技能,在教师的引导下,自行构建模型,然后通过类比,优化模型,找到解决问题的途径,将起到事半功倍的成效.广大农村数学教师要进一步研究并使用这种工具.在运用几何画板的时候,要充分地利用它来引导学生的学习.我们用几何画板绘制图表、图像、图形、动画等来创设直观情境辅助学生思考,而不是代替学生思考.作为教师要给予恰当的提示,通过计算机演示实验帮助学生完成思考过程,形成对知识的理解,而不是利用计算机直接地给出结论[5].否则会使学生一味停留在视觉层面,养成过分依赖的习惯,挫伤学生的创造意识和实践能力.

5 结论

信息技术与数学课程整合,不是简单地把信息技术仅仅作为辅助教师教学的演示工具,而是要实现信息技术与学科教学融合.通过对初中数学课堂教学中几个典型事例的分析,我们可以发现: 几何画板能更好地创设问题情境,激发学生数学学习的兴趣,自主地参与到学习与研究之中;几何画板能动态地展示教学内容,揭示数学问题的本质;几何画板利用进行数学实验,能提高课堂教学效率,有效地促进学生数学水平和能力的提升.信息技术与数学课程的融合,还有很多值得探讨的课题,我们仍在研究的路上.