动面问题中的重叠面积函数的教学设计

广东省惠州市惠阳区华南师范大学附属惠阳学校(516211) 郑素萍

广东省惠州市惠阳区教育局教研室(516211) 钟文辉

1 内容解析

初中几何中的动面问题是中考的热点和难点,此类题综合性强,渗透了分类讨论、转化、数形结合等数学思想.研究此类问题,对培养和发展学生数学核心素养有重要影响.

2 教学目标

2.1 知识目标通过本节课学习,学生熟练掌握几何中图形平移和三角形相似、等边三角形性质、特殊三角函数和二次函数解析式等知识,通过例题的学习和变式训练,体会到建立函数模型是描述动面问题的重要手段,是转化为代数问题的关键桥梁.

2.2 技能目标

(1)掌握动面问题中求重叠面积函数的基本思路: 确定动面运动方向——寻找动面特殊位置——分类讨论画出各类图形——寻找特殊的边角关系——建立各类面积函数关系式;

(2)掌握表示面动函数的方法: 动中取静,以静制动,用点动表示线动,用线动表示面动.

3 教学疑难点分析

借助特殊三角函数求角度、用代数式表示动点运动过程中动线的边长以及动面的面积,不重不漏地讨论运动过程中的图形的变化,及其对应的线段关系和面积关系.

4 教学支持条件分析

为了让学生更直观地分析动面的运动情况,确定特殊点,可用几何画板辅助观察.

5 教学过程设计

5.1 教学流程图如下

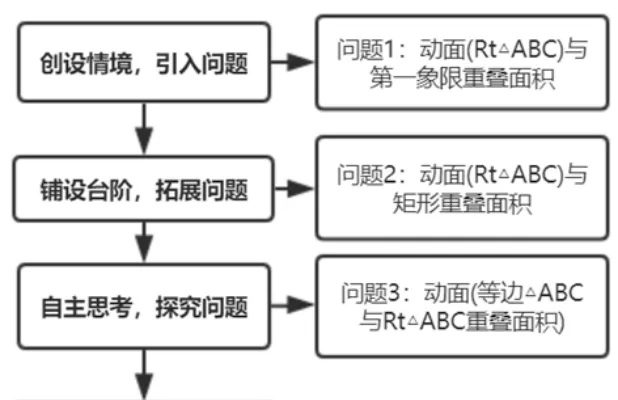
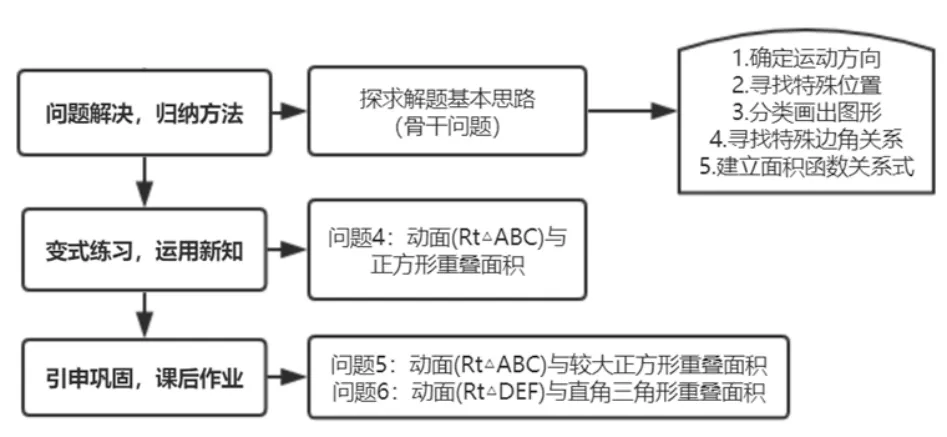
5.2 教学过程

5.2.1 创设情境,引入问题

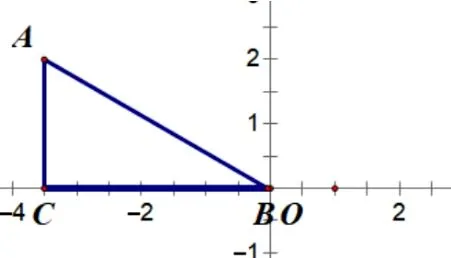
问题1(自编辅例题)如图, 在平面直角坐标系中,直角三角形ABC从O点出发,以每秒一个单位长度的速度,沿x轴正方向运动;其中,∠C= 90°,AB= 4,BC=线段BC落在x轴上;设运动时间为t秒,ΔABC与第一象限重合部分面积为S(平方单位),求S与t的函数关系式.

【解题思路】 确定动面运动方向(沿x轴正方向运动) ——寻找动面特殊位置(分界线y轴) ——分类讨论画出各类图形(如图1-1、如图1-2) ——寻找特殊的边角关系(cos∠ABC=可得∠ABC= 30°)——建立各类面积函数关系式.

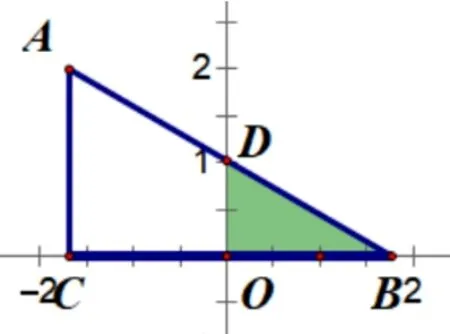
图1-1

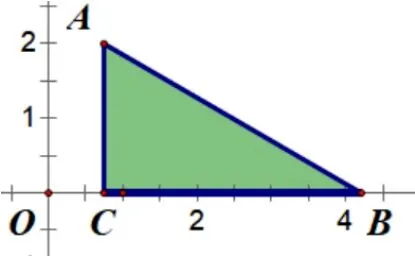
图1-2

【设计意图】问题1 设计直角三角形的平移问题引入,精选范例,构架函数模型,学生初步掌握分类讨论的关键是通过动手操作画图,理清各种情况.同时掌握通过特殊三角函数值,发现特殊的边角关系.

5.2.2 铺设台阶,拓展问题

问题2(自编辅例题) 在问题1 的情境下, 增加条件:如图,四边形OEFG为矩形,设ΔABC运动过程中与矩形OEFG重叠部分面积为y,求y与t的函数关系式.

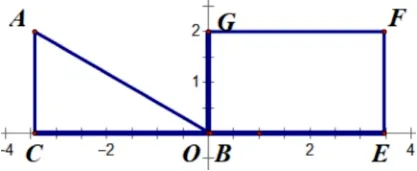
【解题思路】 确定动面运动方向(沿x轴正方向运动)——寻找动面特殊位置(分界线y轴、EF)——分类讨论画出各类图形(如图3、如图4) ——寻找特殊的边角关系可得∠ABC= 30°)——建立各类面积函数关系式.

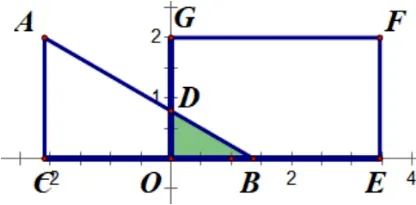
图2-1

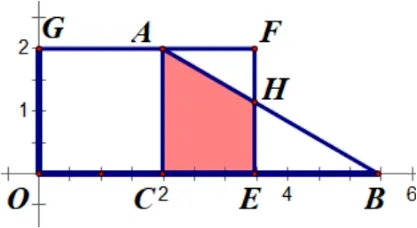
图2-2

①当点B在y轴右侧、EF左侧时, 如图2-1;S=②当点B在EF右侧时,如图2-2;

【设计意图】问题1 到问题2,由直角三角形与无边界的第一象限的重叠面积,变式为求解直角三角形与有边界矩形的重叠面积, 逐步变式设问, 提高难度, 激发学生的求知欲,突破难点“利用相似和锐角三角函数知识,用变量t表示线段的长”,探究一题多解提高学生的解决综合问题的能力.

通过对问题1、问题2 的解决后进行反思,引导学生梳理“动面问题中求重叠面积函数”解题基本思路确定动面运动方向——寻找动面特殊位置——分类讨论画出各类图形——寻找特殊的边角关系——建立各类面积函数关系式.

5.2.3 自主思考,探究问题

问题3(第二届广东省中小学青年教师教学能力大赛初中数学决赛说题比赛题目)如图,矩形ABCD的两边AB、BC的长为方程的两个解(AB ＞BC),点E在CD上,且DE:EC= 2 : 1,AC交BE于点F.平行于AB的直线l从A点出发,以每秒1 个单位长度的速度沿A →D方向平移,到点D时停止.直线l与线段AC,BE分别相交于M,N两点,以MN为边作等边ΔMNF,点F在线段MN下方.设直线l的运动时间为t秒,MN的长度为y(单位长度),ΔMNF和ΔABC重叠部分的面积为S(平方单位).

(1)求BC、CE的长度;

(2)求y与t的函数关系式,求当t=2 时,y的值;

(3)求S与t的函数关系式.

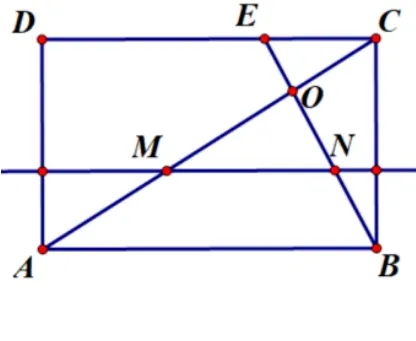
【解题思路】

(1) 解方程, 得x1= 4,x2=

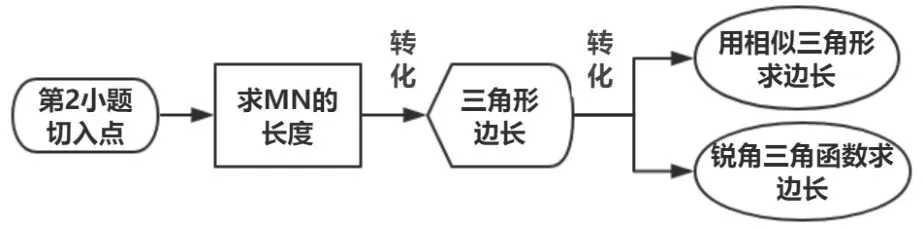
(2) 由ΔOAB∽ΔOCE, 可得三角形对应高之比等于相似比, 从而OH= 3,OI= 1; 确定动线运动方向(沿A →D方向平移) ——寻找动线特殊位置(分界点O点,t=3)——分类讨论画出各类图形(如图3-1、图3-2)——寻找特殊的边角关系——建立各类线段函数关系式(方法1: 借助三角形相似的性质;方法2: 借助锐角三角函数).

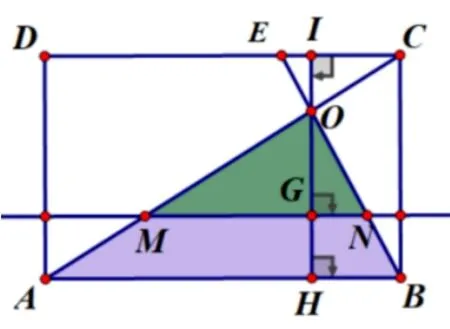
图3-1

图3-2

(3)确定动面的运动方向(沿A →D方向平移)——寻找动面特殊位置(分界线1:F点在线段AB上(如图3-3);分界线2:MN运动到过O点(如图3-4))——分类讨论画出各类图形(如图3-5、图3-6、图3-7)——寻找特殊的边角关系——建立各类线段函数关系式(方法1: 借助三角形相似的性质,方法2: 借助锐角三角函数如图3-8,图3-9、图3-10、图3-11、图3-12).

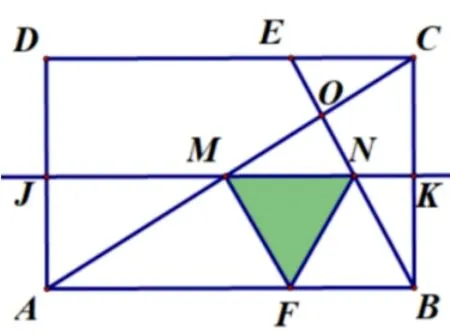
图3-3

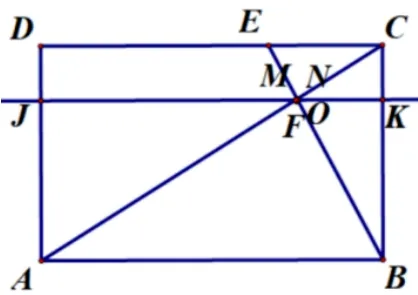
图3-4

图3-5

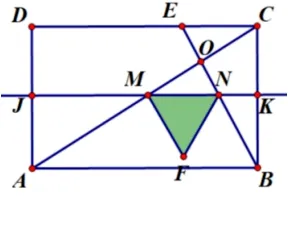
图3-6

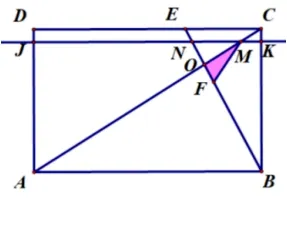
图3-7

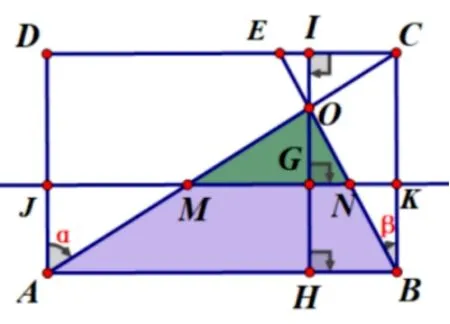
图3-8

图3-9

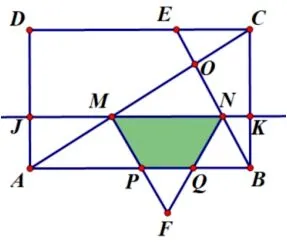
图3-10

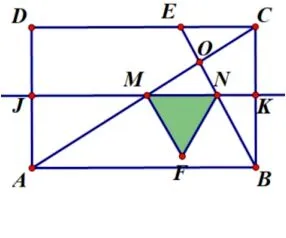
图3-11

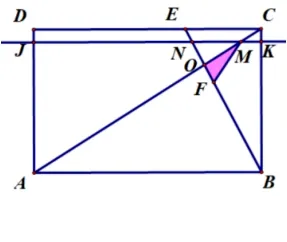
图3-12

5.2.4 问题解决,归纳方法

【议一议】通过上述问题的处理,说说处理动点问题中面积计算(最值)问题分哪些步骤进行? 可以采取什么方法解决这个问题? 涉及到哪些数学思想方法?

(1)动面问题中求重叠面积函数的一般步骤:

(2)动中取静,以静制动: 图形运动变化的过程中,蕴含着某些固定的边角关系,通过相似三角形,三角函数可以表示出所需的边角关系.

(3)将面动转化为线动,线动转化为点动: 利用点动轨迹表示出线段长度,用线段长表示出面积大小.

(4)寻找分界线的标准: 运动状态发现变化的临界线就是边界,既要考虑运动图形的最前端,又要考虑图形的最末端;有多个多界的时候,每个边界都要考虑.

5.2.5 变式训练,运用新知

问题4(问题2 变式)在问题2(辅例题) 的情境下, 将矩形OEFG进一步特殊化, 改成正方形OEFG, 边长为2,其他条件不变,求重叠面积y与t的函数关系式.

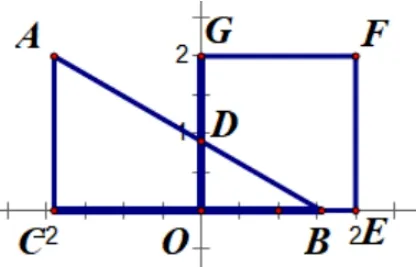
【解题思路】确定动面的运动方向(沿x轴正方向平移)——寻找动面特殊位置( ①点B与点E重合; ②点C与点O重合; ③点C与点E重合)——分类讨论画出各类图形(如图4-1、图4-2、图4-3)——寻找特殊的边角关系——建立各类线段函数关系式(方法1: 借助三角形相似的性质,方法2: 借助锐角三角函数).

图4-1

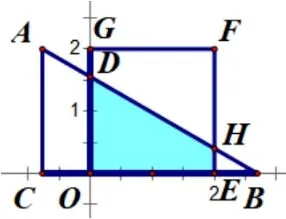
图4-2

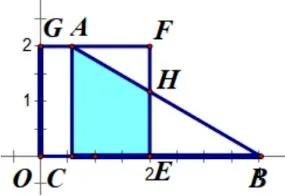
图4-3

【设计意图】熟练运用“动面问题中求重叠面积函数”的一般解题思路解决问题,内化学生的技能,突出中考的重点、突破难点,培养学生一题多解、通性通法和综合能力,让学生体会分类讨论思想、数形结合思想、转化思想以及建模思想.

5.2.6 引申巩固,课后作业

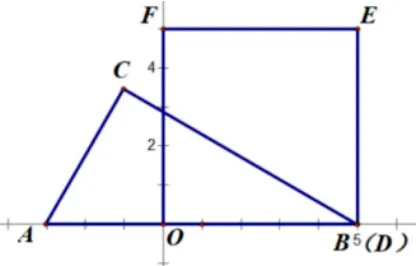
问题5(《新课程学习辅导》九年级下册学业水平考试模拟卷一,2019)如图,在平面直角坐标系中, RtΔABC和正方形GDEF的其中一条边都在x轴上,其中点G与原点O重合,∠C= 90°,AC= 4,点A、B的坐标分别为(−3,0),(5,0).若将RtΔABC沿x轴正方向以每秒1 个单位长度的速度平移,当顶点C落在线段DE上时停止移动.

(1)在没有开始移动RtΔABC时,BC与FG交于点M,求∠MBE的度数.

(2)在移动RtΔABC的过程中,求顶点C恰好落在四边形GDEF的边上所需要的的时间.

(3)在移动RtΔABC的过程中,设RtΔABC与正方形GDEF重叠部分面积为S,移动的时间为t(t ＞0)s,求S关于t的函数解析式.

【解题思路】分类讨论画出各类图形:

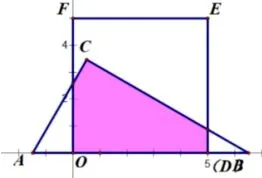
图5-1

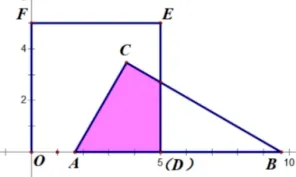
图5-2

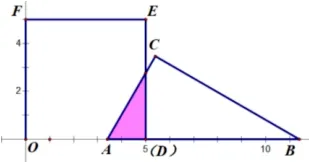
图5-3

【设计意图】

问题5 是问题4 的进一步变式,将直角三角形直角边与x轴重合,变式为斜边与x轴,同时,将正方形的边长放大,进一步让学生理解分类讨论思想(讨论不同时刻重叠图形的变化)、转化思想(四边形面积转化为三角形面积)、数形结合思想和函数模型.

问题6(2019 年惠州市惠阳区青年教师解题比赛第25题)RtΔABC与RtΔDEF的位置如图所示, 其中AC=∠D= 90,其中,RtΔDEF沿射线CB以每秒1 个单位长度的速度向右运动,射线DE、DF与射线AB分别交于点N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.

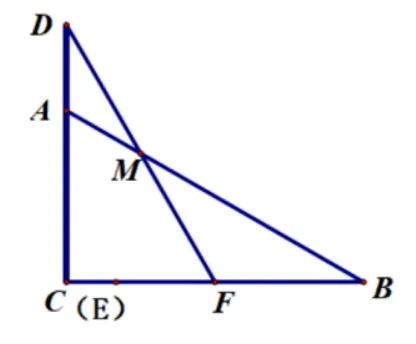
(1)当RtΔDEF在起始时,求∠AMF的度数;

(2)设BC的中点为P,当ΔPBM为等腰三角形时,求t的值;

(3)若两个三角形重叠部分面积为S,写出S与t的函数关系式和相应自变量的取值范围.

【解题思路】分类讨论画出各类图形

(2)等腰ΔPBM的三种情况:

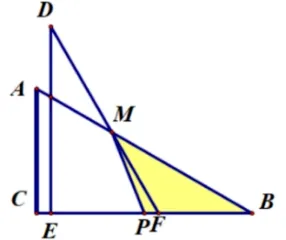
图6-2-1

图6-2-2

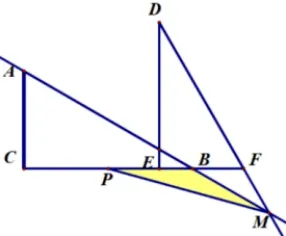
图6-3-3

(3)重叠面积变化

图6-3-1

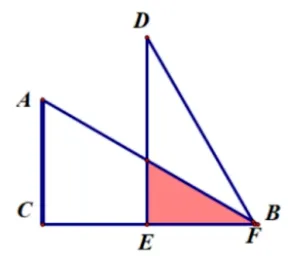
图6-3-2

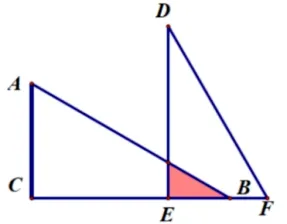
图6-3-3

【设计意图】

问题6 是问题3 和问题4 的变式引申,将问题4 中固定不动的矩形变为直角三角形,将问题3 中的动等边三角形变为直角三角形,运用“动面问题中求重叠面积函数”解题基本思路解决问题,进一步内化为学生解题的技能,培养学生解决问题的综合能力.

问题7(自编)如图, ΔABC是边长为4 的等边三角形,点D是BC边上的中点,连接AD.点E是射线AC上的一个动点,沿A →C方向,以每秒1 个单位长度的速度运动,设点E运动时间为t秒.

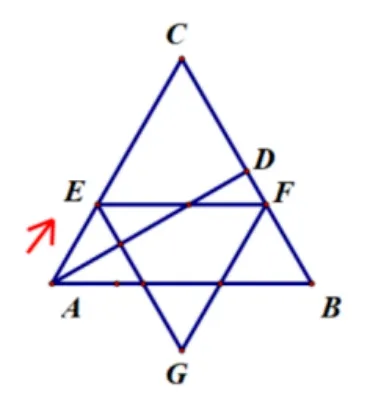
图7-1

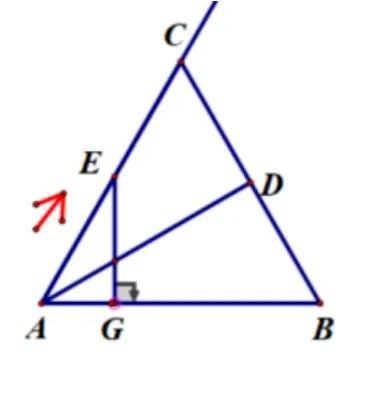
图7-2

(1)过点E作EF//AB,交BC于点F,以EF为边长,构造如图所示的等边ΔEFG;ΔEFG与ΔABD重叠部分面积为y,求y与t的函数关系式.

(2)过点E作EF ⊥AB,交AB于点F,设ΔAEG与ΔABD重叠部分面积为S,求S与t的函数关系式.

【解题思路】分类讨论画出各类图形

(1)等边ΔEFG与直角ΔABD重叠的几种情形:

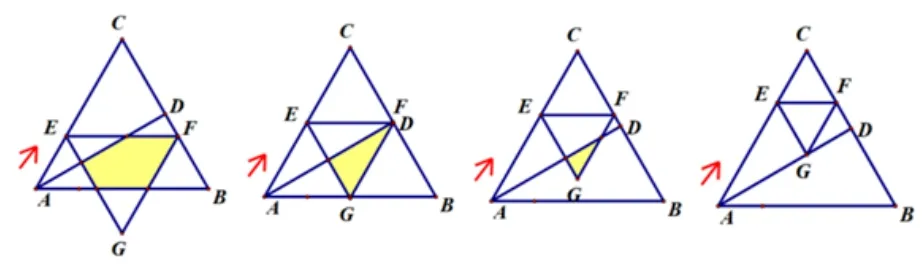
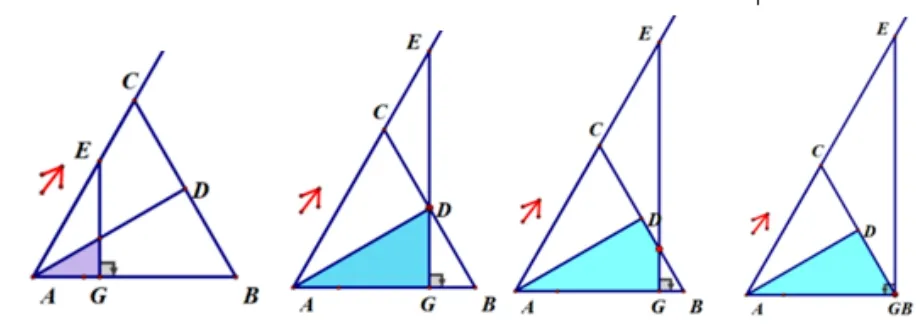
【设计意图】

问题7 是通过动点E,引起线段EF的运动,构造动面等边ΔEFG;从而分类讨论动等边三角形与定直角三角形重叠面积函数.且将点在线段AC上运动,纵向迁移到点在射线AC上运动,进一步拓展学生的思维.

6 教学反思

(1)在日常教学中注意提升学生的计算能力,培养学生简化运算的意识;

(2)在中考疑难问题的教学注意搭设梯子,逐级增加难度,让学生够得着、学得到,增强数学学习的信心与兴趣;

(3)可以进一步对例题进行变式,不断拓展问题的深度和广度.