“球的体积公式及其应用”的教学设计、实践与反思

上海市格致中学(201401) 林佳乐

上海市黄浦区教育学院(200023) 徐庆惠

1 教学目标和教学重点、难点

1.1 教学目标

(1)会运用祖暅原理推导球的体积公式; 会解决与球的体积有关的问题.

(2)经历运用祖暅原理构造辅助体的过程,体会化归与转化的数学思想;对球体积公式的应用,加强空间想象能力及运算能力.

(3)感受数学的文化价值,发展探索精神.

1.2 教学重点

利用祖暅原理推导球的体积公式;球与正方体、正四面体的几个特殊的位置关系的问题.

1.3 教学难点

构造符合祖暅原理条件的几何体的过程.

2 教学过程(片段)

2.1 探究新知

已知球的半径为R,求球的体积V.

师: 我们需要利用祖暅原理,祖暅原理中关键是两个几何体底面积相等,高相等,而球没有底面,所以我们先来求半球的体积.

问题1: 我们根据祖暅原理,来推导半球的体积公式,那么我们需要构造一个怎样的几何体呢? 这个几何体需要满足什么条件呢?

生1: 在任意等高处用一组平行平面去截两个几何体时,截面面积相等.

师: 那么也就是说这两个几何体符合祖暅原理的条件对不对?

生2: 对的.

师: 好,另外该几何体体积应该可求的,所以我们需要借助熟悉的几何体.该几何体与半球夹在两个平行平面之间,即要求该几何体与半球等高.

(ppt 展示)我们知道该几何体高应该是R,当用平行于底面的任意一个平面去截半球,我们思考下所得的截面面积如何求? 设截面与底面之间的距离为h(0＜h ＜R),我们用已知R和h表示面积S1,

师: 首先想想看截面是什么图形?

生2: 是圆.

师: 那么这个圆的面积S1如何表示?

生2:S1=πr2=π(R2−h2).

师: 我们看这是两项的差πR2−πh2, 可以表示什么图形的面积差呢?

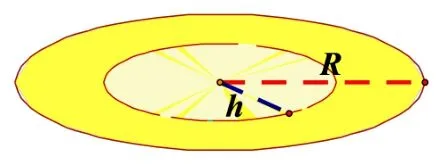
生2: 表示圆环的面积.

师: 非常好,具体来说这是两个半径分别为R和h的圆的面积之差,即圆环的面积.(ppt)

师: 而截面为圆的几何体我们会想到什么几何体?

生: (部分同学)圆柱和圆锥.

师: 好的,那么我们来看同底等高的圆锥和圆柱,观察同底等高的圆锥、半球、圆柱,这三个截面,(h变化时截面变化几何画板动态演示)

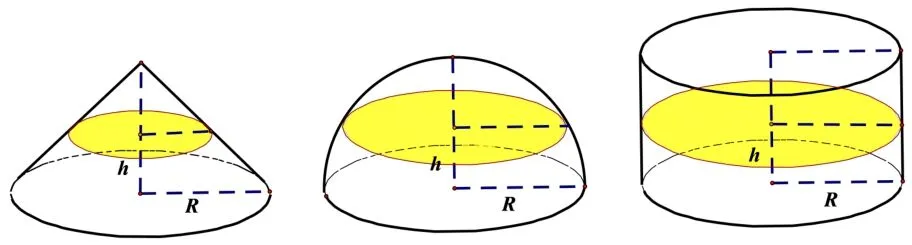
我们发现圆柱截面面积是不变的,而圆锥的截面面积随着的增大而减小,接下来同学小组讨论一下,构造怎样的截面使得截面面积是πR2−πh2呢? 请同学们构造一下这个几何体.

问题2:πR2表示圆柱的截面,那么πh2这个圆在哪里?

学生小组讨论

师: 你们找到πh2了吗?

生3: 这个几何体应该是圆柱里面挖去圆锥.

师: 能不能说明为什么?πh2在哪里?

生3: 圆锥的截面面积.

师: 圆锥的顶点和截面上的点分别为P和O,那么圆锥的半径是多少?

生3: 是h.

师: 我们知道这个圆锥比较特殊,底和高均为R,所以母线和高所成的角为45°,PO等于多少?

生3:R −h,哦,半径是R −h.

师: 对的,所以面积并不是πh2对吧.

生3: 嗯…是的(思考中)

师: 我们来看,如果圆锥的截面半径刚好是h就是我们需要的,那就是说圆锥的顶点到截面的距离应该是h,而我们知道截面距底面的距离为h,即圆锥顶点应该在底面所在平面上,这说明什么呢?

生3: 哦…需要圆锥倒过来放.

师: 非常好,我们把圆锥倒过来放,这是截面半径为h,那么截面面积为πh2对吧.(结合ppt)

师: 因此随着截面高度h变化时,截得圆锥的截面圆的半径始终是h, 圆柱的截面面积与圆锥的截面面积之差为S1=πR2−πh2和半球截面面积始终相等.

我们构造的几何体是与半球同底等高的圆柱挖去一个同底等高的倒置圆锥而组成的几何体.(圆锥移到圆柱中几何画板动态演示).

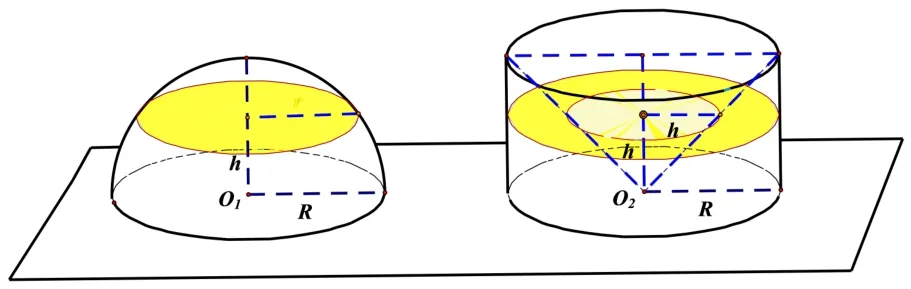
由祖暅原理,我们知道半球的体积与构造出的几何体体积相等,而这个由圆柱挖去圆锥构造出的几何体体积我们如何求?

生4: 半球的体积等于圆柱的体积减去圆锥的体积(教师板书)V半球=V柱−V锥=πR3−

师: 很好,我们利用祖暅原理得出了球的体积公式,那么运用公式时只需知道球的半径.接下来我们一起来研究和球体积有关的问题.

2.2 应用提升

例设正方体的棱长为a,求

(1)正方体内切球的体积;

(2)正方体外接球的体积;

(3)与正方体的棱都相切的球的体积.

师: 大家思考下内切球满足什么条件?

生5: 内切球球心到各个面的距离相等.

师: 球心在哪里?

生5: 在正方体的中心.

师: 很好,所以半径为…

生5: 半径等于正方体棱长的一半,

师: 很好, 所以代入体积公式可得内切球体积V1=我们也可以画出截面图形是这样的(ppt).

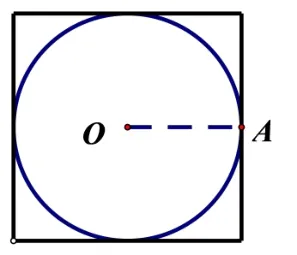
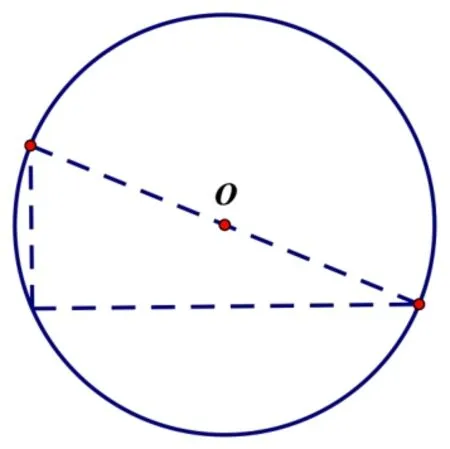
师: 接下来请你再思考下,正方体外接球呢?

生5: 我认为正方体外接球球心还是正方体的中心,半径是球心到各个顶点距离,R=也可以求出体积.

师: 非常好,截面图形是这样吧(ppt).

师: 接下来我们思考,如果球与正方体各棱相切,想象一下,这个球怎样能做到和正方体各条棱都相切?

思考30s

师: 能不能请一位同学给大家描述一下.

生6: 我觉得球心仍然是正方体的中心…(思考片刻)

师: 既然相切,切点位置在哪里?

生6: 切点在正方体棱的中点.

师: 对不对? 也就是说球心到各棱中点距离是相等的对吧,所以切点是各条棱的中点!

(教师拿出空的正方体教具演示)我们可以想象这个正方体中我们有一个气球, 在吹这个气球过程中, 我们要把气球理想化想象成球体, 则气球逐渐变大过程中, 到某一时刻气球与各条棱均相切了, 所以我们求半径即求球心到各棱中点的距离,容易求得的.(ppt)如图所示,连接AB,因此该球的直径大小为面对角线长度则

小结: 正方体与球的几种位置关系,需要确定球心位置,切点位置,转化到平面图形中,求出半径.内切球半径为球心到正方体各个面的距离,大小等于棱长的外接球半径为球心到正方体各个顶点的距离,大小为正方体体对角线的与各棱相切的球的半径为球心到各棱的距离,大小为正方体面对角线的(如图)

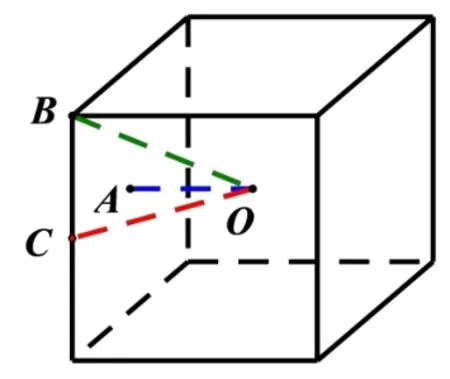
变式: 如果把正方体改为正四面体,设各棱长为a,三种情况下球的体积又为多少?

【设计意图】本例题是关于球与正方体、正四面体的几个特殊的位置关系的问题,是对球的体积公式的应用,也是对正方体、正四面体中寻找基本量所在的平面图形的巩固.从中体现类比、转化的思想方法.

(学生画图求解,教师板书画图)

师: 我们需要如何找到这三种情况下的半径呢?

生7: 先确定内切球球心位置.

师: 非常好,球心在哪里?

生7: 球心在正四面体的高AN上.

师: 对的! 大家观察老师用3D 打印这个正四面体和内切球,当然其中一面是没有开放不封闭的,我们从这个角度观察,球心应该在正四面体的高上对吧?

师: 那么在各个面的切点在哪里?

生7: 在底面的切点为三角形的中心.

师: 在图中用字母表示(如图所示)M,N分别为切点,所以内切球半径为?

生7: 半径为ON或OM.

师: 我们再看外接球的半径是什么?

(思考片刻…)

生7: 线段OA.

师: 能不能解释下? 我们知道O是内切球球心,你的意思是O也是外接球球心? 能不能说说原因.

生7: 是的, 因为AM=DN,OM=ON, 所以RtΔAOM和RtΔDON全等,所以OA=OD.

师: 很好, 那么与OB,OC相等为什么呢? (教师连接OB,OC)

生7: 因为BN=CN=DN,所以三个直角三角形全等,所以OB=OC=OD.

师: 具体是哪三个直角三角形全等?

生7:三角形ONB,ONC,OND全等.

师: 非常好, 请坐! 我们知道ON是公共的直角边,BN=CN=DN,所以OB=OC=OD.

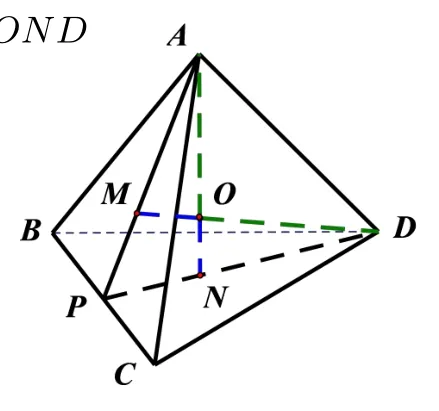
那么也就是说内切球球心也是外接球球心,那么大家思考下是不是与棱相切的球的球心呢?

(部分同学回答: 是的)

师: 没错,此时球心也是O,我们可以证明的.那么与棱相切的切点在哪里?

(部分学生回答: 棱的中点)

所以我们所求半径是哪条线段?

生8: 可以取AD的中点Q,OQ是半径.

师: 很好,还可以是哪条线段?

生8:OP.

师: 对的! 请坐! 那么我们看,这三个半径我们都可以转化到哪个平面图形中求解呢?

(学生齐声回答: 平面APD中)

师: 对的! 那么ΔAPD又是一个什么三角形呢?

(部分学生答道: 等腰三角形! )

师: 没错! 由于AP=PD,这个等腰三角形三边已知,那么我们要求的三个半径如果能求出其中一个,另外两个是否可求呢?

(学生点头)

师: 好,那么我们再思考,例题中是正方体与球的几种特殊的位置关系,那么正四面体与正方体之间有没有什么关系呢?

(部分学生回答: 正四面体可以放入正方体中)

师: 有同学说可以放入正方体中,也就是说,正方体中有没有正四面体?

(学生齐声回答: 有的)

(教师ppt 展示正方体中的正四面体)

师: 那么我们看,正四面体的外接球和正方体有什么关系?

生9: (思考片刻)也是正方体的外接球.

师: 能解释下为什么吗?

生9: 因为各个顶点都在球上, 球心到各个顶点距离相等.

师: 很好! 所以半径应该可以求出来喽,正四面体的棱长为a,那么正方体的棱长为…

生9: 正方体棱长为然后体对角线为所以球半径为

师: 嗯! 所以代入体积公式可求体积对吧! 那么我们再思考下, 正四面体与棱相切的球和正方体有什么位置关系吗?

生10: 正四面体与棱相切的球是正方体的内切球!

师: 很好! 他认为这个球是正方体的内切球,(ppt 展示),切点在棱的中点也就是正方体的各个面的中心对吧,所以这个球与正方体的各面相切,是内切球! 从而我们也可以求出半径和体积对不对? (学生点头)

师: 那么相应的正四面体的内切球半径通过外接球或者与棱相切的球的半径可求,大家课后思考下,正四面体的内切球半径还可以通过什么方法求解吗?

小结: 通过对正四面体内切球,外接球,与棱相切的球的研究,我们发现,内切球半经为球心O到等腰三角形APD腰的距离, 外接球半径为球心O到等腰三角形APD底边顶点的距离,与棱相切的球的半径为球心O到等腰三角形APD顶点的距离或底边的距离,这三种情况均可以转化到平面图形中去解决.而内切球半径与外接球半径之和为正四面体的高.另外,可以将正四面体放入正方体中,转化到正方体和球的位置关系进行相应计算.

2.3 课堂小结

我们来总结一下今天所学的内容:

我们利用祖暅原理推导出了球的体积公式,在构造几何体时要符合祖暅原理的条件,通过圆柱挖去倒置的圆锥来求出半球的体积,从而得出了球的体积公式.另外应用球的体积公式解决相关问题,球与正方体、正四面体的三种位置关系下的体积计算,关键是确定球心,找到切点,转化到平面图形中求出不同情况下球的半径.

3 教学反思

3.1 关于课堂的环节

(1)“球的体积公式”是教材中“由祖暅原理和圆柱、圆锥的体积公式可得球的体积公式”这样一句话带过,而笔者认为,祖暅原理的应用的重要性可以从课本中基本的公式的推导体现,因此将根据祖暅原理推导半球的体积公式的整个过程呈现在课堂中,希望学生在经历公式推导的过程中,加深了对祖暅原理的理解,体会其中蕴含的数学思想方法.另外,对于构造符合祖暅原理条件几何体也是一个开始,后面可以根据学生的能力对高考题目中出现的祖暅原理的应用进行拓展训练,培养学生自主探究解决问题,对任何事物要养成知其然而更知其所以然的习惯.

(2)公式推导过程中,学生在教师的引导下,一步步完成构造与半球体积相等的几何体,这也是本节课的难点,实际上在构造几何体时,符合祖暅原理条件的可能不是圆柱中挖去圆锥,可以构造四棱锥等方法求解,所以如果这一环节能够大胆放手让学生自主构造,培养学生主动探索的精神,同时也可以课后让学生自己再构造一个几何体,注重知识的发生.

(3)求正四面体的内切、外接、与棱相切的球的半径时,球心相同,这个地方也是需要严格证明的,由于课堂时间以及重点内容的关系, 这个说理过程可以课前或者课后说明.而通过教具模型的展示,学生应该可以从直观上观察得到这个结论.

(4)正四面体中的三个半径均转化到等腰三角形中求解,而这三个半径已知任意一个半径,可求出其他两个半径,因此将三种情况一起考虑,可以先将正四面体的情况转化为正方体的情况来求解.而在求内切球半径时可以利用等体积方法求解,可以作为课后思考让学生自主探索研究完成.

3.2 立体几何教学中提升核心素养的思考

(1) 立体几何不光是空间想象能力, 空间逻辑推理、分析、说理的能力同样重要

立体几何的教学,往往很多人认为只要学生能想出来即可,然而立体几何中不光要有空间想象能力,对于空间中的逻辑推理,说理能力要求才是真正体现核心素养的地方.核心素养中的“直观想象”中也要蕴含逻辑推理、分析说理等素养.

(2)在日常教学中培养学生的核心素养,渗透数学思想方法

核心素养的培养与三维目标的建立、数学思想方法的渗透、数学能力的培养等是息息相关,应该体现在日常的教学中,需要我们教师不断思考,从日常教学中能够体现核心素养的内容,掌握好方式方法,尤其对于立体几何是提升直观想象素养的重要载体,而本节课中数学抽象、数学运算(转化为平面图形中计算相关问题)、逻辑推理(构造几何体的截面面积与半球的截面面积相等)等核心素养也相应得到体现,这些需要在日常教学中不断渗透和培养.