藏在巧合背后的秘密

【摘要】文章从一道课堂例题出发，发现学生使用错误解法却凑巧得出了正确答案，并且这种错误解法能凑巧答对许多类似的题目，由此展开了一番探究，并得出了一般性的结论。

【关键词】不等式  整体代换  线性规划  动态扫描

【中图分类号】G633.6   【文献标识码】A 【文章编号】2095-3089（2021）18-0126-03

一、巧合产生

在教授人教A版必修5《3.1不等关系与不等式》这节内容时，笔者选用了一道例题作为课内探究题（当时学生还未学习线性规划的相关内容），该例题如下：

例1  已知函数f（x）=ɑx2+bx满足1≤f（-1）≤2，2≤f（1）≤4，求f（2）的取值范围。

本题在不使用线性规划作图求解的情况下用整体代换的方法求解如下：

解法1  设f（2）=αf（1）+βf（-1）=（α+β）ɑ+（α-β）b，

因为f（2）=4ɑ+2b，所以α+β=4

α-β=2 ，可得α=3

β=1，即f（2）=3f（1）+f（-1）.

又由1≤f（-1）=ɑ-b≤2

2≤f（1）=ɑ+b≤4，得7≤f（2）≤14.

课堂上笔者请了一位学生上黑板板演，他的做法如下：

解法2  因为1≤f（-1）=ɑ-b≤2

2≤f（1）=ɑ+b≤4，两式相加得3≤2ɑ≤6

又由4≤2ɑ+2b≤8， 所以f（2）=4ɑ+2b=2ɑ+（2ɑ+2b），得7≤f（2）≤14.

他得到的答案是正确的，班里还有一部分学生也是用这种方法做的。那么他们的解法对吗？细究他的解题过程可以发现，他借助的是ɑ+b的范围与ɑ的范围，而ɑ与ɑ+b实际上不独立，它们是相互制约的，即当ɑ+b取到最大值时，ɑ未必取得到最大值。不妨利用线性规划的方法做出本题的可行域。

图1是由已知条件确定的（a，b）的可行域，图2是该学生使用a+b与a的范围所确定的（a，b）的可行域，发现两者不一致。即利用a+b与a的范围会使可行域扩大，所得到的目标函数z=4a+2b的范围也有可能会扩大。但此处目标函数在图1和图2的可行域中，都恰好在点（3，1）处取得最大值，在（1.5，0.5）处取得最小值，所以产生了巧合。假如换一种拆法：

解法3  由1≤f（-1）=ɑ-b≤2

2≤f（1）=ɑ+b≤4 ，可得-3≤-2ɑ≤0，

所以，4ɑ+2b=4（ɑ+b）-2b，所以5≤4ɑ+2b≤16.

此时得到的答案是错误的，因此该学生用这种解法得出的答案虽然正确，却是由于凑巧。

二、投石探路

此时笔者忍不住想，如果更换目标函数，使用上述的“拆分法”是否还会产生巧合？

例2  已知1≤ɑ-b≤2

2≤ɑ+b≤4

（1）求2ɑ+4b的取值范围。

解法1 （整體代换）  由2ɑ+4b=3（ɑ+b）-（ɑ-b），可得4≤2ɑ+4b≤11.

解法2 （拆分法）  由2ɑ+4b=4（ɑ+b）-2ɑ，可得2≤2ɑ+4b≤13.

解法3 （拆分法）  由2ɑ+4b=2（ɑ+b）+2b，可得4≤2ɑ+4b≤11.

（2）求4ɑ-2b的取值范围。

解法1 （整体代换）  由4ɑ-2b=（ɑ+b）+3（ɑ-b），可得5≤4ɑ-2b≤10.

解法2 （拆分法）  由4ɑ-2b=4（ɑ-b）+2b，可得4≤4ɑ-2b≤11.

解法3 （拆分法）  由4ɑ-2b=2（ɑ-b）+2ɑ，可得5≤4ɑ-2b≤10.

（3）求2ɑ-4b的取值范围。

解法1 （整体代换）  由2ɑ-4b=-（ɑ+b）+3（ɑ-b），可得-1≤2ɑ-4b≤4.

解法2 （拆分法）  由2ɑ-4b=2（ɑ-b）-2b，可得-1≤2ɑ-4b≤4.

解法3 （拆分法）  由2ɑ-4b=4（ɑ-b）-2ɑ，可得-2≤2ɑ-4b≤5.

三、柳暗花明

不妨以例2的（1）、（2）为例，来探究其中的奥秘。

（1）求2ɑ+4b的取值范围

如图3，解法2中由a和a+b确定的可行域为▱ABCD。如图4，解法3中由b和a+b确定的可行域为▱EFCH。而由已知条件a+b和ɑ-b确定的可行域为图3或图4中的阴影部分，当目标函数为z=2ɑ+4b时，目标函数确定的动直线b=-ɑ+为图中虚线。由图可知，▱EFCH与阴影部分使目标函数z=2ɑ+4b取到的最大值点都是点F，最小值点都是点H，因此解法3可得正确答案。此处目标函数z=2ɑ+4b确定的直线斜率为-，解法3利用了ɑ+b与b的范围。还可以发现，当目标函数确定的直线斜率在（-1，0）内时，▱EFCH与阴影部分使目标函数取到的最大值点都是点F，最小值点都是点H，因此只要目标函数确定的直线斜率在（-1，0）内，将目标函数拆成ɑ+b与b的组合所得答案必正确。

（2）求4ɑ-2b的范围

图5和图6分别是解法2和解法3确定的可行域，可以发现解法2的可行域为▱ABCD，解法3的可行域为▱EFCH，由已知条件确定的可行域为阴影部分，其中解法3恰好使得目标函数z=4ɑ-2b在点E取到最大值，点G取到最小值，从而解法3得到正确答案。并且，只要目标函数确定的直线斜率在（1，+∞）内，则▱EFCH与阴影部分使目标函数取到的最大值点都是点E，最小值点都是点G，此时将目标函数拆成ɑ-b与ɑ的组合所得答案必正确。

同理，（3）求2ɑ-4b的取值范围中，解法2得到正确答案，目标函数z=2ɑ-4b确定的直线b=ɑ-的斜率在（0，1）内，利用了ɑ-b和b的范围。例1中求4ɑ+2b的取值范围，利用ɑ+b和ɑ的范围得到正确答案，目标函数z=4ɑ+2b确定的直线b=-2ɑ+的斜率在（-∞，-1）内。

因此，可有结论：若已知c≤ɑ+b≤d

p≤ɑ-b≤q求mɑ+nb，（mn≠0）的取值范围。

使用“拆分法”，设k=-，

①k∈（-∞，-1），将mɑ+nb拆成ɑ+b与ɑ的组合，使用ɑ+b与ɑ的范围;

②k∈（-1，0），将mɑ+nb拆成ɑ+b与b的组合，使用ɑ+b与b的范围;

③k∈（0，1），将mɑ+nb拆成ɑ-b与b 的组合，使用ɑ-b与b的范围;

④k∈（1，+∞），将mɑ+nb拆成ɑ-b与ɑ的组合，使用ɑ-b与ɑ的范围;

则所求的取值范围正确。

四、改错为正

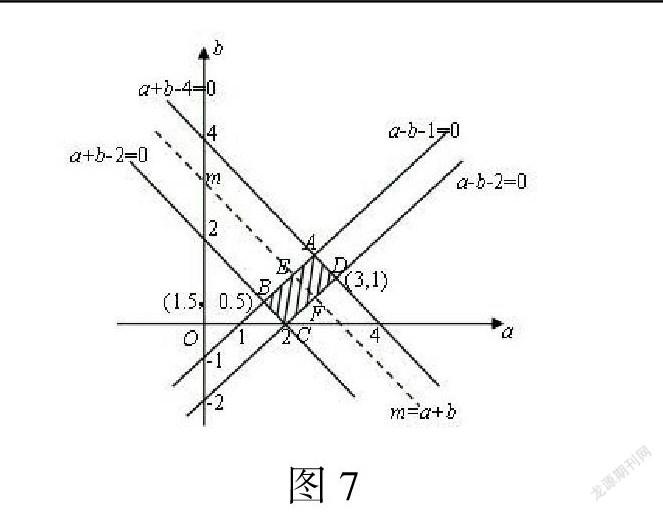
既然有部分学生会把目标函数z=mɑ+nb拆成ɑ±b与ɑ或b的组合，而使用ɑ±b与ɑ或b的范围不一定能得到正确答案，那么如何得到正确答案呢？不妨重新来看例1的解法3，目标函数z=4ɑ+2b=4（ɑ+b）-2b，下面来探究如何获得正确的答案。

解法4  如图7中，可行域中位于线段EF上的点的横坐标、纵坐标满足ɑ+b=m，此时z=4（ɑ+b）-2b=4m-2b，因此目标函数应该在纵坐标最大的点E处取得最小值，在纵坐标最小的点F处取最大值。而当EF所在直线在可行域内运动时，目标函数就在线段AB上取最小值，在线段CD上取最大值。题目就转化为：

（1）已知ɑ-b=1，1，0.5≤b≤1.5，求z=4ɑ+2b的最小值。

将ɑ=b+1代入目标函数得z=6b+4，由0.5≤b≤1.5，可得z=4ɑ+2b的最小值是7.

（2）已知ɑ-b=2，0≤b≤1，求z=4ɑ+2b的最大值。

将ɑ=b+2代入目标函数得z=6b+8，由0≤b≤1，可得z=4ɑ+2b的最大值是14.

上述解法具有可迁移性，适用于把目标函数z=mɑ+nb拆成ɑ±b与ɑ或b的任意组合，保证了“拆分法”的正确性。

五、思考感悟

学生把目标函数z=mɑ+nb拆成ɑ±b与ɑ或b的组合，使用ɑ±b与ɑ或b的范围来求z=mɑ+nb的范围的原因可能有如下几点：一是在等量关系当中经常使用等价代换，所以学生有這样的思维习惯，在类比迁移过程中想要使用代换的思想。二是学生刚开始学习必修5第三章不等式与不等关系，还没有接触线性规划的内容，因此还没建立起可行域的概念，不知道代换过程中可能会引起可行域的改变。三是对不等式的性质理解不透彻，没有认识到变量之间是相互制约的。此外，这种做法的错因，是学生初学不等式时不易理解的地方，也正是教学的重难点。在经历问题分析和解决的过程中，让学生领悟其中所蕴含的数学思想也是教学的一个难点。因此，在解题教学中可以以此作为知识的“生长点”与“延伸点”，让学生落入巧合，产生兴趣，展开探究，得出结论，从数学学习中获得乐趣。师生也能够一起享用数学这一充满智力挑战又饱含乐趣的盛宴。

参考文献：

[1]刘锐.解决线性规划问题的一种新方法及其应用[J].中国数学教育，2016（Z2）：107-108

[2]刘少平，张学礼.线性规划常见错误剖析[J].数理化解题研究，2016（25）：7-9

作者简介：

王聪聪（1991年-），女，浙江温州人，中学二级教师，本科学历。