分布时滞Shimizu-Morioka系统的稳定性及Hopf分岔分析
罗宁宁,管俊彪
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
1963年,Lorenz[1]发现了首个混沌吸引子,此后更多三维自治混沌系统如Chen系统[2]、Lü系统[3]和Liu系统[4]等相继被发现。混沌在工程领域有着重要的应用,对混沌的动力学性质研究一直是非线性科学领域的研究重点。近年来,Shimizu-Morioka系统因其丰富的动力学行为及应用背景得到广泛研究,如文献[5]研究单时滞反馈的Shimizu-Morioka混沌系统,选择时滞作为参数,讨论了系统的稳定性及产生Hopf分岔的条件。文献研究表明,引入单时滞反馈可方便用于混沌系统的稳定性及分岔控制,更一般的分布时滞也被引入混沌系统用于分岔分析[6-8]。本文研究Shimizu-Morioka混沌系统的分布时滞控制,通过引入分布时滞反馈,分别讨论在弱核及强核情形下系统的局部稳定性以及Hopf分岔的存在性问题。
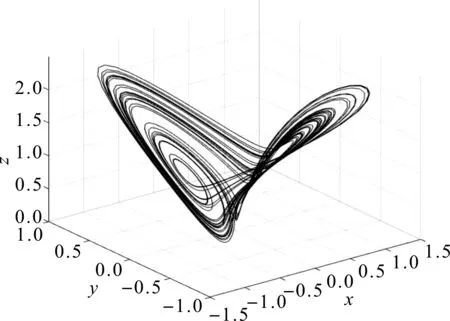
图1 系统(1)混沌吸引子的三维空间相图
1 平衡点的稳定性及Hopf分岔的存在性
Shimizu-Morioka混沌系统为:
(1)
式中,x,y,z为系统变量,a,b为系统参数,当a=0.75,b=0.45时,系统(1)的混沌吸引子如图1所示。
考虑如下分布时滞反馈Shimizu-Morioka系统:
(2)


(3)
改写式(3),得到:
其中,
系统(3)的线性特征方程为:
(4)
以下分别讨论弱核及强核情形下特征方程根的分布情况及平衡点的稳定性。
(1)弱核情形
当k(s)=be-bs,b>0。将其代入式(4),整理得:
λ3+f1(b)λ2+f2(b)λ+f3(b)=0
(5)
式中,
(6)
由Routh-Hurwitz准则,系统(3)所有根有负的实部的充要条件为f1(b)>0,f2(b)>0,f3(b)>0,f1(b)f2(b)-f3(b)>0,记Δ(b)=f1(b)f2(b)-f3(b),Δ为定义在(0,+∞)上的连续可微函数。
在E0处,f3(b)=-b<0,故系统(3)的平衡点E0是不稳定的。由于平衡点E1和E2是对称的,所以,本文仅讨论平衡点E1。在E1处,式(6)可转化为:

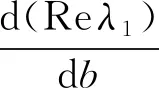
根据上述对平衡点处特征根分布情况的分析,得出以下定理。
定理1若b+a-M>0,a>0,b>0,ab+a2-aM-2>0,a2-aM-2<0,则
(Ⅰ)当b>b+时,平衡点E1和E2为渐近稳定的;
(Ⅱ)当b∈(0,b+)时,平衡点E1和E2为不稳定的;

(2)强核情形
当k(s)=γ2se-γs,γ>0。将其代入式(4),整理得:
λ4+m1(b)λ3+m2(b)λ2+m3(b)λ+m4(b)=0
(7)
其中
由Routh-Hurwitz准则,系统(3)所有根有负的实部的充要条件为:
显然,在平衡点E0和E2处有m4(b)<0,故E0和E2是不稳定的。在平衡点E1处有
定理2若其满足如下条件,系统(2)的平衡点E1是渐近稳定的。
(Ⅰ)2b+a-M>0;
(Ⅱ)(2b+a-M)(b2+2ab-2Mb)-ab2-2b>0;

证明令λ1,λ2,λ,3,λ,4是(7)式的4个特征根,则有:
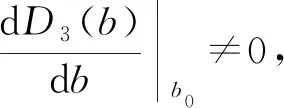
2 数值仿真与分析

采用Mathematic软件进行数值模拟,参数b分别为3.0和2.5时,系统(2)的状态变量随时间t变化的时间序列图和空间相图如图2、图3所示。

图2 a=0.5,M=-1,b=3.0时,系统(2)的相图与时间序列图
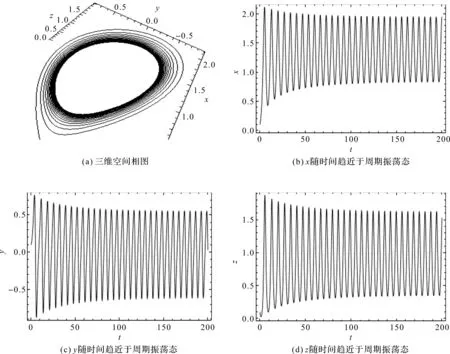
图3 a=0.5,M=-1,b=2.5时,系统(2)的相图与时间序列图
3 结束语
本文研究了具有分布时滞的Shimizu-Morioka混沌系统,利用Routh-Hurwitz准则分析在弱核及强核情形下平衡点的局部稳定性及Hopf分岔的存在性,分析结果可作为混沌控制实现的理论依据。基于此,将进一步研究带分布时滞反馈项控制系统的Hopf分岔动力学行为。

