OFDM-PON系统中基于混沌的细胞自动机加密算法
卓先好,楼丁溧,毕美华,2,胡志蕊
(1.杭州电子科技大学通信工程学院,浙江 杭州 310018;2.上海交通大学光纤区域网与新型光通信系统国家重点实验室,上海 200240)
0 引 言
近年来,随着现代互联网技术的快速发展,各种新媒体服务层出不穷,如超高清视频、物联网、移动多媒体等,社会信息量急剧增加,由于正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术在光纤传输中具有高频谱效率、灵活的资源分配等优点,被广泛应用于下一代无源光网络(Passive Optical Network, PON)的研究[1]。然而,PON系统的下行传播采用广播结构使数据在传输过程中极易遭到非法窃取,一定程度上降低了系统的安全性[2]。因此,为了提高系统的安全性,研究人员对系统的加密算法展开研究,但是,其中主要研究方案都依据传统的网络安全,通过在网络层加入安全协议来提升系统安全,然而针对物理层的报头数据和控制帧数据等信息的保护相对较少。因此,如何通过系统物理层数据的加密,提高系统的安全性是当下研究的热点问题。
由于混沌的强随机性、遍历性和对初始参数的高敏感性,研究者利用混沌对OFDM-PON系统的安全性展开研究。在这些混沌加密方案中,文献[3-4]将混沌映射生成的序列作为混沌选择映射(Chaotic Selected Mapping, CSLM)与混沌部分传输序列(Chaotic Partial Transmit Sequences, CPTS)的相位旋转因子,提高了系统的传输性能和安全性。文献[5]进一步提出了基于二维混沌加密的SLM加密方案,利用二维logistic映射分别产生随机交织器和相位序列对信号加扰,同时进一步提升了系统性能。但是上述方案都需要额外的带宽来传输最优相位因子,增加了系统的复杂性,同时也降低了系统的实时数据处理能力。为了改进,研究者又提出了若干高频谱效率的可靠性传输方案,文献[6]对离散傅里叶变换(Discrete Fourier Transform, DFT)矩阵列置乱,在实现OFDM信号的峰均功率比(Peak-To-Average Power Ratio, PAPR)降低的同时,进一步提高了密文的置乱性。然而,上述方案只关注密钥空间的大小和系统的性能,通过加密得到的密文是固定不变的,当系统遭受选择明文攻击(Chosen-Plaintext Attack, CPA)或者密钥泄漏时,密文极有可能被破解。针对密钥安全问题,文献[7]利用拉格朗日多项式隐藏混沌初始值实现密钥保护;在选择明文攻击中,非法用户可以选择输入的纯文本数据得到相应的密文数据,并通过明密文之间固定的映射关系来破解密文。针对目前方案普遍无法抵抗选择明文攻击和置乱性弱等缺点,本文使用具有高并行性和运算规则简单的细胞自动机(Cellular Automaton, CA)[8],并将其优异的非线性与动态加密方案相结合。因此,本方案提出一种基于混沌序列与细胞自动机相结合的加密方案,进一步提高OFDM-PON系统的安全性。
1 OFDM-PON系统加密原理
基于细胞自动机的OFDM-PON系统加密方案原理如图1所示。加密算法主要由3个步骤构成:第一步,利用3维Chen混沌系统生成混沌序列,混沌序列控制初等细胞自动机的状态环,产生的状态环与伪随机二进制序列(Pseudo Random Binary Sequence, PRBS)进行异或;第二步,数据经过串并转换和正交幅度调制(Quadrature Amplitude Modulation, QAM)映射,利用二维细胞自动机的状态转移规则对QAM符号矩阵进行置乱加密,并进行相应的异或扩散加密;第三步,利用混沌序列随机插入同步序列实现接收端的定时同步。

图1 OFDM-PON系统数据加密发送端原理图
为了提高系统的安全性,本文采用三维Chen氏混沌系统产生加密所需的混沌序列,其表达式如下[9]:

(1)
式中,x,y,z为混沌序列的数值,a,b,c为混沌系统的控制参数,通过Lyapunov指数可以判断系统产生的数值是否具有混沌特性,当a=35,b=3,c=28可得Chen氏混沌系统的3个Lyapunov指数分别为λ1=2.007,λ2=0,λ3=-19.233,该系统存在正的Lyapunov指数,可以验证了该系统的混沌特性[10]。当Chen氏混沌初始值x0=0.271 8,y0=0.453 3,z0=0.782 6,式(1)通过五阶龙格-库塔法循环求解[11],以时间步长h=0.001经过1 000次迭代后,得到3组混沌序列{xn},{yn},{zn}。产生的混沌序列不适合直接进行加密,需要进行预处理,混沌序列进行取整,利用混沌序列的随机性得到数字混沌整数序列{Dx,n},{Dy,n},{Dz,n}用于系统加密,其中数字混沌整数序列的生成过程如下:
(2)
式中,函数Extract(xn,m,n,p)表示提取数值xn的小数部分的第m,n,p位数,并且由这些数依次排列成整数。由于利用MATLAB产生的数字混沌系统的数字精度为10-15,并且数字混沌系统具有很好的初值敏感性[11],设置m=13,n=14,p=15。在这些设置下,产生的混沌序列{Dx,n}具有良好的随机性。mod(a,b)表示返回a除以b的余数,数据通过取模运算后,生成的混沌序列能够在一定数值范围内(0~M-1)具有良好的随机性。由于初等细胞自动机(Elementary Cellular Automaton, ECA)在规则42下存在8个具有不同周期的状态环[12],在本方案中设置M=8。本方案中,利用生成的数字混沌序列{Dx,n}随机选择初等细胞自动机的状态环集合中的状态环。对于每个状态环,利用生成的数字混沌序列{Dy,n}用于随机状态环的状态转移。利用生成的数字混沌序列{Dz,n}随机插入同步序列实现接收端的定时同步。
1.1 基于初等细胞自动机状态环的加密算法
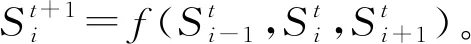
d⊕state(1)⊕state(2)⊕…⊕state(k)=d′
(3)
式中,⊕表示逻辑异或操作;d,d′分别表示明文二进制序列和经过循环特性后状态;state(i),1≤i≤k表示状态环中第i个细胞的状态,明文经过若干个状态环实现明文的状态转移从而实现加密。异或操作从状态环中的任何状态开始,假设明文序列d经过状态环进行m次异或操作得到密文序列,在解密端使用相同状态环经过剩余的k-m次状态转移(异或操作),则可以得到原明文序列。
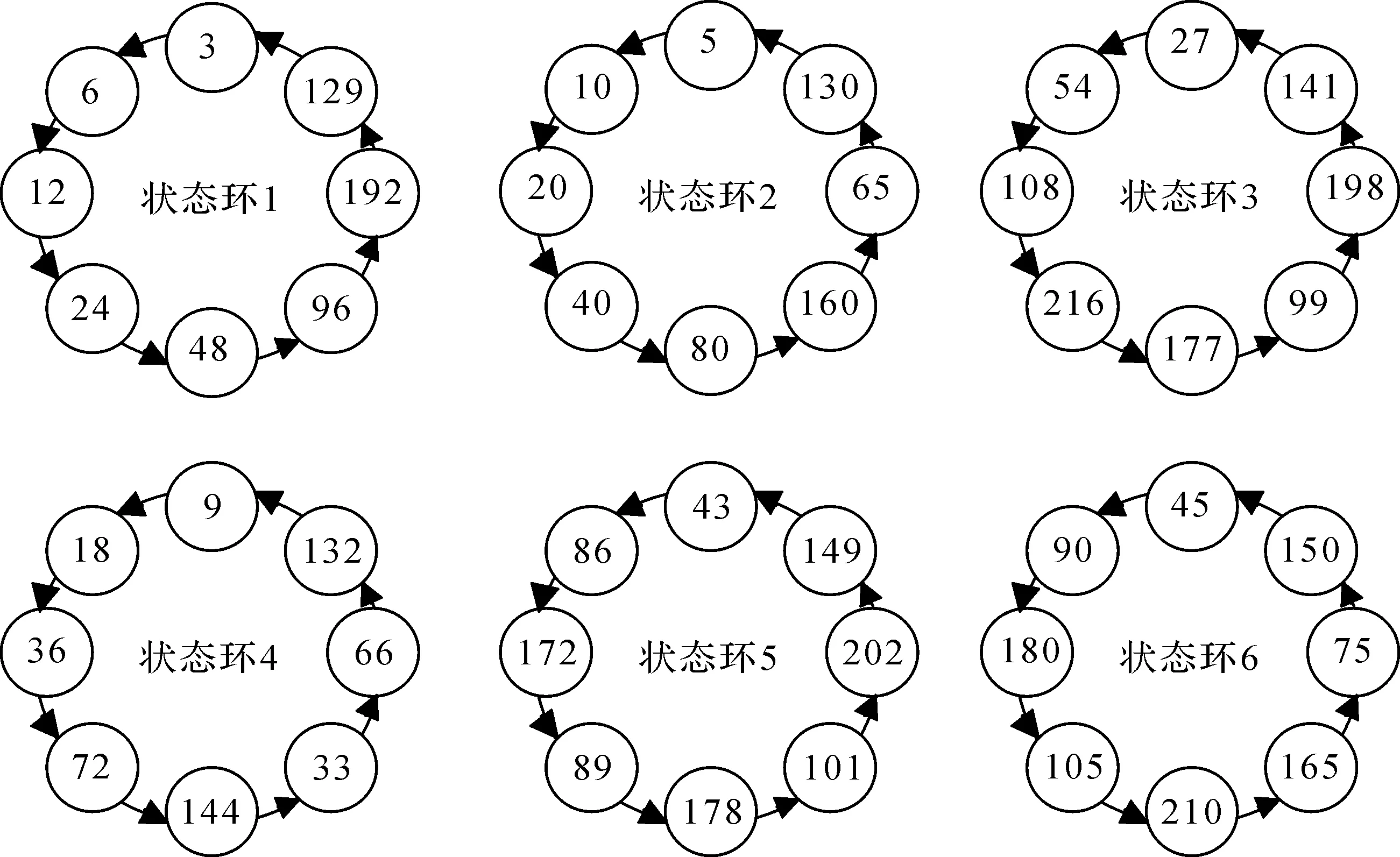
图2 初等细胞自动机在规则42下的部分状态转移图
在基于ECA状态环的加密算法过程中,将输入数据PRBS序列按照每3位为一组的规则进行转换,并将3位二进制序列转化为十进制,该数作为一维CA状态环的输入进行状态转移,从而实现数据加密。具体的加解密过程如下:
加密:(state ringj=1,…,8)pi⊕statej(1)⊕statej(2)⊕…⊕statej(m)=ci
解密:(state ringj=1,…,8)ci⊕statej(m+1)⊕statej(m+2)⊕…⊕statej(8)=pi
(4)
式中,pi和ci分别表示输入每一组的明文和密文,利用混沌序列{Dx,n}和{Dy,n}分别控制上式中的j和m,可以随机选择CA状态环种类集合中的状态环,以及随机选择每组数据进行转移的次数。如图2所示,每个状态环的状态都是8种,并且状态转移为周期循环转移。因此,在进行数据解密时,接收数据需要确定每组数据使用的状态环以及相同的混沌序列。在接收端,每组数据在相同状态环上进行8-m次状态转移,可以解密得到原始数据。该方案利用ECA将混沌序列的随机性扩散到明文中,从而实现数据加密。本文方案的一维细胞自动机加密,若需要破解,除了需要获得混沌序列,还需要获得相应的状态环集合,进一步增大了密钥空间。
1.2 基于二维细胞自动机的矩阵加密算法
二维细胞自动机与一维细胞自动机的相似,二维细胞自动机是矩形的细胞网络,由M×N个细胞组成,C(i,j)表示为第i行、第j列的细胞,每个细胞只有2个状态{0,1}。每一个细胞的状态更新需要相邻细胞的状态和转移函数共同决定。因此,每个细胞的状态方程可以表示为:
(5)

(6)
式中,变量C,N,W,S,E的取值范围为{0,1},根据这些变量判断相邻的细胞是否对该细胞的状态转移产生影响,若取值为0,则代表无影响,若取值为1,则代表有影响。X表示局部转移规则为线性规则或者非线性规则(0为线性规则,1为非线性规则),根据相邻细胞的影响和局部转移规则可以实现细胞状态值的更新。由于系统进行传输中,进行QAM映射产生QAM符号,本方案利用二维CA状态转移进行QAM符号的置乱,可以降低原始数据的相关性,提高系统的安全性。
本方案采用的时大小为2×2的CA,根据Von Neumann模型,本方案设计一种状态转移规则,可以实现CA在两种状态之间进行周期循环,状态转移规则表达式为[14]:
(7)
大小为2×2的CA总共包含16种状态,如图3所示,给出了部分状态的转移图。每种状态经过一次状态转移后,与原始状态会有较大的差距。
基于二维细胞自动机的加密算法具体实现过程如下:原始数据经过初等细胞自动机状态环的加密后,进行串并转换将二进制数据转换成十六进制数据;然后进行16-QAM映射,产生一个N×M的QAM符号矩阵,然后对符号进行二进制编码。如图4(b)所示,给出了QAM符号二进制映射示意图。QAM符号矩阵通过二进制映射转换为大小为N×4M二进制矩阵。然后利用二维CA的状态转移进行加密。如图4(a)所示,将二进制矩阵依次看作一个2×2的二维CA,利用等式(7)的状态转移规则对二进制矩阵进行加密。每次递增一行并且按照“Z”型依次进行状态转移。由于二维CA的特性,二进制矩阵中任意两行之间都会产生状态间的关联。因此,矩阵中任意一个符号发生变化将会引起相邻行的符号变化。
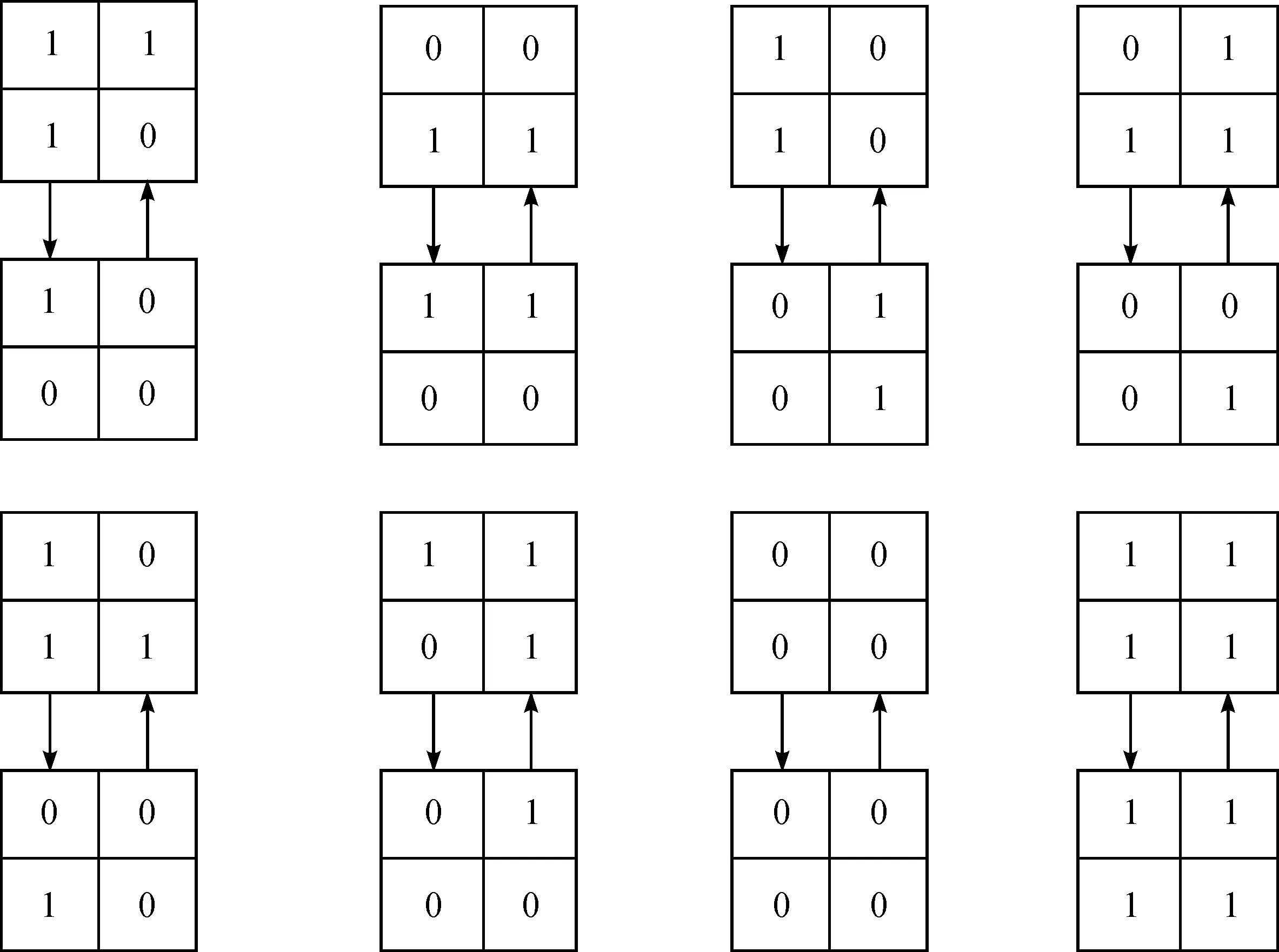
图3 大小为2×2的二维细胞自动机状态转移图

图4 二维细胞自动机置乱原理示意图
在接收端,通过信道估计获取QAM符号矩阵,将N×M的QAM符号矩阵进行相同的二进制编码。由于解密过程为加密过程的逆过程,数据解密需要从二进制矩阵的最后一个2×2的矩阵开始进行逆向操作。本方案采用的二位CA的状态集只有两种状态,因此,接收端只需要根据等式(7)进行一次状态转移,可以实现数据解密恢复出原始数据。
2 实验与结果分析
OFDM-PON加密传输系统实验设置如图5所示,实验仿真装置主要包括三个部分:发射端、接收端和光纤信道。在发射端,利用MATLAB进行数字信号的加密和OFDM信号调制。原始信号为PRBS信号,原始信号与基于混沌序列的ECA状态环进行异或,实现原始数据的第一次加密。然后进行串并转换、16-QAM映射,之后利用二维CA对QAM符号进行置乱加密。为了接收端的信道估计,需要在OFDM符号中插入块导频,导频间隔为10。然后进行快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT),其中IFFT的长度为512,子载波数为128。在进行IFFT前,OFDM符号矩阵需要进行Hermitian对称处理,可以使IFFT信号变换为实值信号。插入循环前缀(Cyclic Prefix, Cp)可以有效的降低码间干扰,本方案采用OFDM信号长度为1/8的CP。利用混沌序列对OFDM信号进行同步。加密的OFDM信号作为光线路终端(Optical Line Terminal, OLT)中的传输信号发射给光网络单元(Optical Network Unit, ONU)。在光纤信道中,该部分主要是在OptiSystem中进行,将加密OFDM信号输入到采样速率为20GSa/s的任意波形发生器(Arbitrary Waveform Generator, AWG)中,实现数字信号到电信号的转换。然后将OFDM信号输入到马赫曾德调制器调制器(Mach-Zehnder Modulator, MZM)进行电光调制,可以生成光OFDM信号。其中MZM的光源为中心波长为1 550 nm的连续波激光器。光OFDM信号输入到掺铒光纤放大器(Erbium Doped Fiber Application Amplifier,EDFA)中,进行10dBm的放大,之后输入到20 km标准单模光纤(Standard Single-Mode Fiber,SSMF)进行传输。在接收端,本方案设置3个ONU,其中两个分别用来接收原始数据和加密数据,另一个为非法用户,用于检测加密方案的有效性。接收到的数据通过光电二极管(Photo-Diode,PD)将光OFDM信号转换为电信号,然后进行信号采样生成数字信号。将OFDM信号输入到MATLAB中。信号进行混沌同步、去CP以及信道估计。之后进行信号的解密、16-QAM解调和串并转换,输出原始信号。
图5 OFDM-PON加密传输系统实验设置
为了验证本方案用于加密算法的混沌序列是否具有较好的随机性。本文采美国国家技术标准局NIST推出的软件包STS对混沌序列进行了随机性测试。该软件主要是利用概率统计对混沌序列进行分析,判断混沌序列是否满足随机特性,从而判断混沌序列是否随机。NIST测试主要包括发生器的选择、二进制序列的产生与执行测试套件这3个主要步骤。其中测试套件包含15种测试项目。NIST提供了两种评判序列随机性能的依据,一是P-Value值测试序列的均匀分布特性,首先给定序列通过测试的显著性水平α=0.001,通过序列的概率学统计获取P-Value值。当P-Value值大于0.01时,说明测试序列的分布是均匀的,即通过测试。二是序列的通过率,统计出所有序列满足条件一的组数。结合这两个条件判断混沌序列的随机性。

表1 三维Chen混沌序列NIST测试结果
本文选取混沌序列小数部分的8~10位,生成总长度位为614.4 Mbits的二进制序列,共分为256段数据流,每段2.4 Mbits进行测试。通过测试标准可以得出,当二进制序列被分为256段时,项目的通过率大于0.9713即可证明序列的随机性。混沌序列的NIST随机性测试如表1所示。从表1可以看出:所有的测试项目均得到较高的P-Value测试值,说明三维Chen氏混沌序列的均匀分布特性;除Rank测试(二进制矩阵阶测试)外,其余项目均有较高的通过率,说明三维Chen混沌系统生成的混沌序列具有良好的随机性,可以作为密钥序列应用于信息加密。
为了进一步验证基于ECA和二维CA加密算法是否具有抗选择明文攻击能力,本文通过观察原始明文的改变对密文的变化量的影响,实验结果如图6所示。图6(a)表示原始明文信号发生1 bit的改变,图6(b)为对应密文变化量。在发送端,当原始明文发生细微变化后,这些细微的变化经过ECA和二维CA加密算法后,混沌序列的随机性扩散到明文中,并且QAM符号间产生了关联。原始信号细微变化造成OFDM信号的每一个子载波上的信号都发生变化,进一步证明了基于ECA和二维CA的加密方法具有良好的扩散性能,可以实现动态密文来抵抗选择明文攻击,提升了系统的安全性。

图6 OFDM符号在改变一位1 bit位下的变化情况

图7 原始信号和加密信号在OFDM-PON系统中的误码率曲线
为了验证加密算法是否对系统传输性能产生影响,本文给出了系统的传输误码率(Bit Error Rate, BER)曲线,如图7所示,图中为原始数据和加密数据分别在SSMF、背靠背两种传输模式下的BER曲线,以及非法ONU的BER曲线。同时图中给出了接收光功率相同下的接收端星座图,可以看出,非法ONU接收数据的星座图毫无规则。在接收光功率相同下,不管是20 km光纤传输还是背靠背传输,采用细胞自动机加密算法加密的信号相比原始信号有0.8 dB的性能恶化,这是因为细胞自动机加密方案的密文彼此相互关联,在接收端容易引起错误扩散从而造成信号的BER降低。但是为了抵抗极具威胁的选择明文攻击,0.8 dB的性能损失是在可接受范围内。此外,非法ONU未获得相应的混沌序列和加密算法,截取密文在解密后的BER一直在0.5上下。非法ONU无法正确解密原始数据。因此,基于ECA和二维加密方案在提高系统安全性同时不会降低系统的传输性能。
密钥空间的大小直接影响加密系统能否有效防止窃听者的攻击,密钥空间越大,对攻击者的抵抗暴力攻击的能力越高。基于混沌的细胞自动机加密算法密钥空间主要由三维Chen氏混沌系统的初始值、随机选取ECA状态环集合中的第j种状态以及ECA状态转移次数m决定。由于数字混沌系统的表达精度为1015,三个混沌初值可提供1015×1015×1015=1045大小的密钥空间。在本方案采取的规则下,ECA状态环的状态集中一共有8种状态。由于ECA的一个状态环的长度为8,并且状态空间为{0,1},该ECA状态转移次数一共有28=256种。本方案中子载波数为128,OFDM符号个数为1 024,基于混沌序列的ECA状态环加密大约提供1017密钥空间。基于二维CA的符号置乱方案采用Von Neumann模型产生24种全局状态,以及二维CA状态转移集合为8。因此,本文提出方案总共可以提供的密钥空间大小约为1064,目前国内计算速度最快的超级计算机是“神威·太湖之光”,该计算机持续计算速度可以达到每秒9.3×1016次的双精度浮点运算[15]。利用该计算进行暴力穷举攻击,需计算时间约为1040年。因此该方案可以有效抵抗暴力攻击。此外,本方案在实现动态密文的情况下,可以充分置乱密文和降低数据间的关联性,在抵抗选择明文攻击基础上还具有抗统计攻击能力。
3 结束语
本文提出一种OFDM-PON中基于混沌序列的细胞自动机安全加密方案,利用细胞自动机的状态转移特性和混沌序列的随机性来增强系统物理层安全性,且在OFDM调制信号经过20 km的SSMF传输的光电系统中验证了可行性。对于传统异或加密方案密钥空间不足问题,本方案采用细胞自动机状态转移和混沌序列相结合进一步增大了密钥空间;对于传统混沌加密中无法抵抗选择明文攻击问题,本方案通过QAM符号的扩散加密实现动态密文解决了该问题。因此,本方案可被应用于下一代OFDM-PON系统中以提升系统安全性。在接收端,本方案存在错误扩散问题,引起0.8 dB性能损失。如何在保证系统安全性的同时,减少加密方案对系统传输性能的影响是下一步研究方向。

