基于单源点检测的跳频信号混合矩阵估计
王 琳,赵知劲,2,尚俊娜
(1.杭州电子科技大学通信工程学院,浙江 杭州 310018;2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室,浙江 嘉兴 314001)
0 引 言
跳频通信具有截获概率低、抗干扰性能好、保密性强等优点,广泛应用于军用和民用领域,对跳频信号侦察和对抗带来严峻挑战[1]。为了获得跳频信号的有用信息,通常采用盲源分离方法将跳频源信号从混合信号中分离出来[2]。由于混合矩阵中包含源信号到达角信息,因此对其估计是盲源分离的关键。文献[3]提出一种时域滤波法,应用时域信号分量比值的均值求出混合矩阵,减低了算法复杂度,但算法性能有待提高。由于跳频信号具有时频稀疏特性,稀疏分量分析方法比独立分量分析方法更为有效。文献[4]将稀疏分量分析运用于跳频信号欠定盲分离,但忽略了载频及传输时延对混合矩阵估计的影响,实用性较差。文献[5]在时频域上对频率进行K-means聚类,实现了对载频、跳变时刻以及混合矩阵的估计,但算法复杂且混合矩阵估计性能较差。文献[6-8]引入单源点检测准则来筛选单源点,分别结合层次聚类算法、势函数聚类算法和动态数据场聚类算法以提高混合矩阵估计精度和抗噪性能,这些算法均运用聚类中心估计混合矩阵,当信噪比较低或聚类中心之间比较接近时,各簇数据相互交融,导致聚类算法无法准确估计聚类中心个数,即网台个数,同时,也无法将信号载频值与估计出的混合矩阵元素一一对应,以致不能估计混合矩阵。本文采用一跳内载频分割时频矩阵取代聚类算法,实现对网台个数准确估计,提出一种单源点检测方法和改进的势函数,提高了低信噪比下混合矩阵的估计性能。
1 信号模型

图1 均匀线阵示意图
假设接收时间Δt内均匀线阵的M个阵元接收到N个同步正交的跳频源信号,且不同源信号的到达角不同,均匀线阵如图1所示。
图1中,θn为源信号sn(t)的到达角,天线间距为d,d≤λmin/2,λmin=c/fmax,λmin为接收信号的最短波长,c为电磁波的传播速度,fmax为源信号载频的最大值。对同一源信号sn(t),第2个阵元相对于第1个阵元接收信号的相对延迟可以表示为:
(1)
第n个跳频源信号sn(t)表示为:
sn(t)=an(t)ej[ωn(t)t+φn(t)],n=1,2,…,N
(2)
式中,an(t)为sn(t)的基带复包络,ωn(t)=2πfn(t),fn(t)和φn(t)分别为载波频率和相位,j表示虚部。
假设在时延(M-1)τn内信号的幅值、载频和相位都没有变化,即当m=1,2,…,M时,an[t-(m-1)τn]≈an(t),ωn[t-(m-1)τn]≈ωn(t)和φn[t-(m-1)τn]≈φn(t),则第m个阵元的接收信号xm(t)表示为:
(3)
式中,vm(t)为第m个阵元接收到的噪声。
根据式(1)、式(2)和式(3),t时刻M个阵元的接收信号用矩阵形式表示为:
(4)
将式(4)简化为:
x(t)=B(t)s(t)+v(t)
(5)

x(t)=Bs(t)+v(t)
(6)
式中,混合矩阵B是固定不变的,B的第(m,n)个元素bm,n=e-j2πfn(m-1)τn。
2 基于单源点检测的混合矩阵估计算法
将短时傅里叶变换运用于式(6)两侧,得到:
X(t,f)=BS(t,f)+V(t,f)
(7)
式中,X(t,f)=[X1(t,f),…,XM(t,f)]T,S(t,f)=[S1(t,f),…,SN(t,f)]T和V(t,f)=[V1(t,f),…,VM(t,f)]T分别表示为x(t),s(t)和v(t)的时频。
由式(6)可得:
(8)
由式(8)可知,混合矩阵B是范德蒙矩阵(Vandermonde),因此只需应用X1(t,f)和X2(t,f)得到混合矩阵B的第2行元素,再使用范德蒙矩阵的性质直接得到混合矩阵B。
为了降低后续处理的计算量,提高混合矩阵估计性能,去除X1(t,f)中由噪声引起的低能量点,公式如下:
(9)
式中,ε1为去噪阈值,0<ε1<1。
2.1 单源点检测方法
假设时频点(tp,fp)是信号sn(t)的单源点,暂时忽略噪声影响,则接收信号的时频比为:
(10)
根据式(10),推导得到:

(11)
根据式(11),得到单源点检测准则:
(12)
式中,Re[·]表示实部。考虑噪声带来的影响,引入门限ε2以适当放宽单源点检测条件:
(13)
式中,ε2为检测阈值,0<ε2<1。当(t,f)满足式(13)时,则为单源点。
2.2 时频图分割法
根据跳变时刻对时频矩阵进行分割,并分别对每一跳进行载频估计。以第1跳为例,令X1(t1,f)为时频矩阵X1(t,f)第1跳。令B0(f)为在频率点f处所有时间点的时频矩阵元素X1(t1,f)的绝对值之和。通过提取峰值来降低频谱泄漏的影响。
(14)
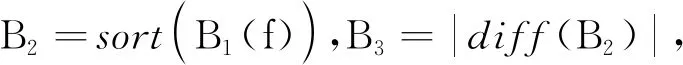

图2 时频矩阵分割
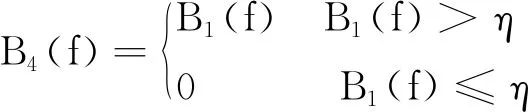
(15)
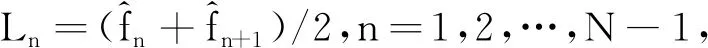
2.3 混合矩阵估计
根据式(10),分别对属于各频率簇Cn的单源点(tp,fp)求时频比的角αi:
(16)
式中,ln为属于频率簇Cn的单源点个数。
为了适应不同信噪比环境,本文提出的自适应势函数表示为:
(17)
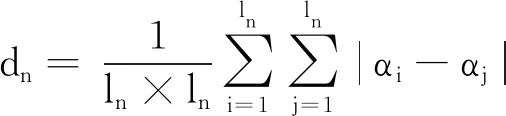

所以第1跳的混合矩阵估计表示为:
(18)

(19)
3 仿真实验与性能分析

根据式(8)得到第一跳的混合矩阵为:

(20)
3.1 参数确定

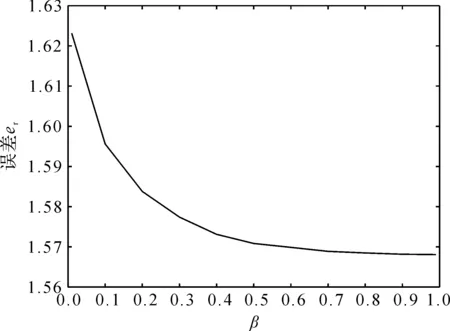
图3 不同β值的估计误差

图4 3个簇的势函数曲线
定义混合矩阵估计归一化均方误差(Normalized Characterized by the Mean Square Error,NMSE)为:
(21)

在时频矩阵未去噪前提下,分析单源点检测阈值ε2对本文算法的影响。在不同信噪比下,ε2取0.1,0.3和0.5时,100次仿真得到混合矩阵估计的归一化均方误差如图5所示。从图5可以看出,当ε2太大时,单源点筛选效果差,混合矩阵估计性能不好。当ε2=0.1时,估计性能较好,故选取ε2=0.1。

图5 阈值ε2对NMSE的影响
3.2 性能分析
3.2.1 单源点检测对时频比数据聚集性的影响
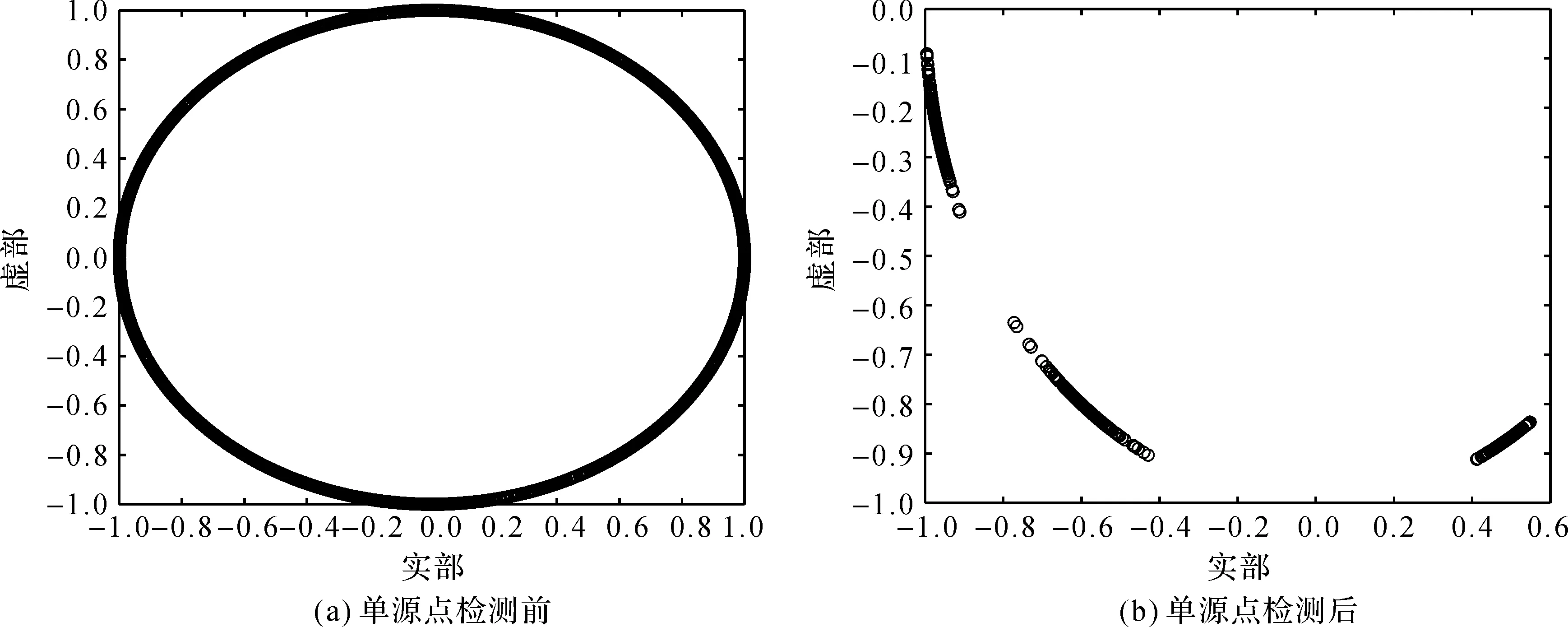
图6 时频比散点图
3.2.2 势函数对混合矩阵估计的影响

图7 势函数性能比较
实验中,分别运用本文势函数和文献[7]势函数来估计混合矩阵。归一化均方误差如图7所示,图7中曲线是100次实验结果的平均值。由图7可以看出,本文势函数性能优于对比势函数。
3.2.3 不同算法性能比较
不同信噪比下,分别采用本文算法和文献[7]算法进行100次仿真实验,得到网台个数估计正确率和混合矩阵估计的归一化均方误差分别如图8和图9所示。由图8可以看出,当信噪比低于-2 dB时,本文算法的网台数估计准确率远高于文献[7]算法。在低信噪比下,各簇数据相互间混杂导致文献[7]算法的聚类功能失效,不能准确估计网台个数;而本文算法根据载频个数来估计网台个数,载频信息在时频矩阵中表现明显,且受低信噪比影响相对较小,估计正确率更高。由图9可以看出,本文算法与文献[7]算法的NMSE曲线均随信噪比的增加而减少,在网台数估计正确的前提下,本文算法的混合矩阵估计精度相对要高一些。

图8 网台数估计正确率

图9 混合矩阵估计NMSE
4 结束语
在低信噪比情况下,本文提出的时频单源点检测方法可以更准确地筛选时频点,时频矩阵分割方法解决了聚类算法在各簇数据混杂时容易失效问题,有效提高了低信噪比下网台数和混合矩阵的估计精度。下一步将针对异步跳频网台的分选展开重点研究。

