一种改进K-means聚类的近邻传播最大最小距离算法

王美琪 李 建

(西南石油大学计算机科学学院 四川 成都 610500)

0 引 言

初始聚类中心对K-means聚类结果影响极大。经典的K-means聚类算法采用随机选取初始聚类中心的方式，有以下不足：① 易导致聚类结果的不稳定；② 有取得离群点作为初始聚类中心的可能；③ 某些初始聚类中心可能离群体太远，有的初始聚类中心可能相互之间隔得太近。为克服这些缺点，文献[1-3]分别采用构造最小生成树、最短路径加权属性图、最大最小距离MMD(Max-Min Distance)算法计算K-means的初始聚类中心，获得了一定的效果。但实验发现，在聚类簇数较大时，因k值的限定，MMD算法获得的初始聚类中心有同类多点而导致初始类的缺失，虽然K-means算法通过迭代移动聚类中心部分最后接近实际中心，但仍有部分将陷入局部最优。且MMD初始聚类中心往往在簇的边界，这无形中影响了算法收敛速度。近邻传播算法(Affinity Propagation，AP)可根据相似参考度进行全局寻优，获得多个具有代表性的聚类中心[4-5]，但由于选到同类多点而导致聚类数目一般大于实际簇数，直接用AP聚类中心作为K-means初始聚类中心聚类的结果不符合实际。

本文提出一种近邻传播算法和最大最小距离算法联合计算K-means初始聚类中心的算法(APMMD)。该算法首先通过近邻传播算法从整个样本集中全局寻优，获得Kap(Kap>k)个具有代表性的候选中心点，再利用最大最小距离算法从Kap个候选中心点中选择k个初始聚类中心。将该算法获得的初始聚类中心应用于K-means聚类，在多个UCI数据集上进行实验，通过已知分类对比，用Purity、AC、NMI、JC、RI和FMI有效性评价指标及迭代次数验证。结果表明，APMMD算法获得初始聚类中心应用于K-means聚类，聚类结果与已知分类十分吻合，有效性评价指标极高，迭代次数明显降低，同时不受聚类簇数的限制。

1 经典的K-means聚类算法

K-means聚类算法是一种经典算法，算法简单、快速，对处理大数据集，该算法保持可伸缩性和高效性。该算法的主要流程：

设X={x1,x2,…,xn}为已知数据集，X中的x1,x2,…,xn为n个数据对象，每个数据对象都是N维数据，即xi=[vi,1,vi,2,…,vi,N]，算法要找到含有k个聚类中心的集合:

C={c1,c2,…,ck}=

{[v1,1,v1,2,…,v1,N],[v2,1,v2,2,…,v2,N],…,[vk,1,vk,2,…,vk,N]}

目标函数表示为：

(1)

式中：d(ci,xj)表示聚类中心与数据对象的欧氏距离，其计算式为：

(2)

算法把数据集划分成使目标函数为最小值的K个类。具体步骤为：首先利用随机选取从数据集中抽取K个数据对象作为初始聚类中心；然后计算剩余数据对象与各个聚类中心的欧氏距离，按照距离最小原则来划分类别;完成一轮聚类后，再计算每一类的平均值，用K个平均值作为新的K个聚类中心，再计算剩余的数据对象与这K个聚类中心的欧氏距离，再按照距离最小原则划分类别，循环反复，直到满足某个终止条件停止迭代。

算法存在以下问题：

(1) 初始聚类中心随机选取，聚类结果不稳定。

(2) 易选到噪声数据和孤立点而陷入局部极值。

(3) 当选到不合理的初始聚类中心时，算法通过迭代移动聚类中心部分最后接近实际中心，部分将陷入局部最优。

2 相关算法

2.1 近邻传播算法

近邻传播算法(AP)由Frey等[6]于2007年提出。AP算法将所有样本都看成潜在的聚类中心，在迭代过程中不断通过节点之间的“信息传递”搜寻具有代表性的聚类中心。AP算法不设置聚类中心的个数，但需要事先设置相似度的参考度，参考度的大小决定聚类中心的个数；参考度一般设为相似度矩阵中所有值的最小值或者中位数，参考度越大则说明各数据点成为聚类中心的能力越强，最终聚类中心的个数则越多。

“信息传递”：将n个数据点之间的相似度组成相似度矩阵s(n,n)，并以对角线上的值s(i,i)作为第i个数据点能否成为聚类中心的评判标准。r(i,k)表示从i点发送到k候选聚类中心的消息，a(i,k)表示k从候选聚类中心发送到i的数值消息。r(i,k)反映点k是否适合作为i点的聚类中心，a(i,k)则反映i点是否选择k作为其聚类中心，称为吸引度和归属度。r(i,k)与a(i,k)越强，则k点作为聚类中心的可能性越大，并且i点隶属于以k点为聚类中心的聚类的可能性也越大。通过迭代而不断地更新每一个点的吸引度和归属度值，直到产生多个高质量的聚类中心，同时将其余的数据点分配到相应的聚类中。

算法可根据参考度获得数据集中具有代表性的多个聚类中心，对数据的初始样本不敏感，聚类中心不会选到离群点，代表性点不会在类的边界，但会有同类多点而导致聚类数目往往大于实际簇数现象。

2.2 最大最小距离算法

最大最小距离算法(MMD)是模式识别中一种基于试探的聚类算法，它以距离(欧氏)为基础，取尽可能远的样本作为聚类中心[7]。首先选择距离最远的两个样本作为第一、第二个聚类中心，再选择未被作为聚类中心的样本与已选中心点之间距离最小中最大点作为下一个聚类中心。依此方法直到产生所需的k个聚类中心。

MMD算法可根据数据集簇数，快速求取指定的k个聚类中心，获得距离较远的样本作为初始聚类中心，但可能选到离群点。聚类簇数较大时，因k值的限定，求取的聚类中心会有同类多点而导致初始类的缺失，选择的中心点一般在类的边界，K-means算法虽然通过迭代移动聚类中心最后接近实际中心，但是无形中影响了算法收敛速度，甚至影响聚类结果。

3 APMMD算法

3.1 基本思路

首先通过AP算法从整个样本集中获得Kap(Kap>k)个具有代表性的候选中心点，再利用最大最小距离算法从Kap个候选中心点中选择k个初始聚类中心。AP对数据的初始样本不敏感，不会选到离群点，也不缺失类别，代表性候选点不在该类的边界，主要问题是因同类多点而导致聚类数目大于实际簇数问题。MMD算法可根据数据集簇数，快速求取指定的k个聚类中心，获得距离较远的样本作为初始聚类中心。AP候选点中类内的点距离要小于类间点距离，通过MMD可去掉AP同类多出的点，从而获得代表性的k个最优聚类中心点。

3.2 算法解析

APMMD算法求取K-means初始聚类中心的过程如图1所示，假设整个样本对象点如图1(a)所示(x1,x2，…，x16，共计16个样本对象点，x5为异常点)，要将样本集划分为3个簇(k=3)。

首先根据AP算法原理，给定参考度从整个样本点获取具有代表性的聚类中心，设获得5个吸引度和归属度(r(i,k),a(i,k))较强的AP候选中心如图1(b)所示，v1=x9，v4=x6，v5=x10，v3=x7，v2=x8，x6和x10、x7和x8在同一簇均具代表性(同类多点)。

再根据MMD算法获得初始聚类中心。如图1(c)所示，设v1和v4距离为d1；v1和v3距离为d2；v1和v2距离为d3，v1和v5距离为d4;v4和v2距离为d6；v4和v3距离为d5；v4和v5距离为d7。

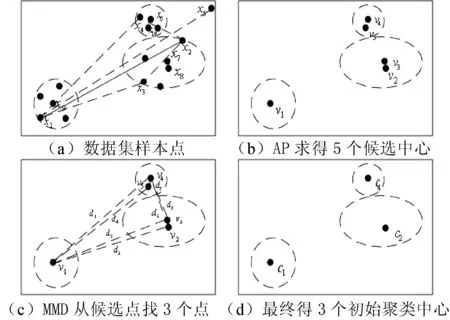
图1 APMMD求取K-means初始聚类中心过程

(1) 选择距离最远的两个样本作为第一、第二个聚类中心，因距离d1为最大，则v1、v4为第一、第二个聚类中心，如图1(d)所示，c1=v1，c4=v4。

(2) 分别比较v2、v3、v5与v1、v4两点的距离，找出距离最小：v2与v1、v4两点的距离最小，选d6；v3与v1、v4两点的距离最小，选d5；v5与v1、v4两点的距离最小，选d7。

(3) 找出v2、v3和v5与v1、v4两点的距离最小中最大的点：d6>d5>d7，即v2作为第三个聚类中心，如图1(d)所示,c2=v2。

3.3 算法步骤

设X={x1,x2,…,xn}⊂RP为n个需聚类的样本。

步骤1定义聚类数目k，选择AP相似参考类型，给定θ∈[0,1]。

步骤2计算数据点的相似度矩阵，计算式为：

s(i,k)=-d2(xi,xk)=-‖xi-xk‖2

(3)

步骤3计算样本点间的吸引度，如下：

r(i,k)=s(i,k)-max{a(i,k′)+s(i,k′)}k≠k′

(4)

步骤4计算样本点间的归属度，计算式为：

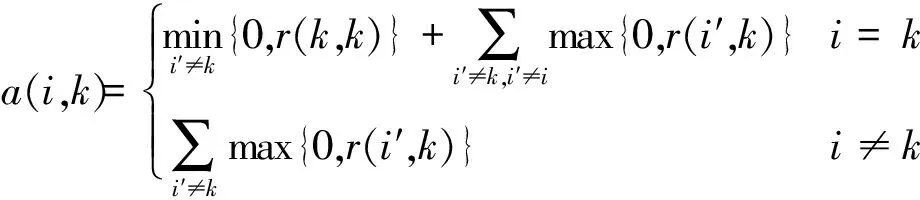
(5)

步骤5更新吸引度、归属度。

ri+1(i,k)=λ×ri(i,k)+(1-λ)×ri+1(i,k)λ∈[0,1)

(6)

ai+1(i,k)=λ×ai(i,k)+(1-λ)×ai+1(i,k)λ∈[0,1)

(7)

步骤6迭代次数超过既定的次数或聚类中心变化较小时结束迭代计算，获得聚类中心Vkap={v1,v2,…,vkap}。否则返回步骤4继续迭代计算。

步骤7从vkap个对象样本中找出距离最大的两个点作为第一、第二个聚类中心，c1=v1，c2=v2。

步骤8计算vkap个对象样本到c1和c2的聚类Di1和Di2，计算c1到c2的距离D12。

步骤9Di=max{min(Di1,Di2)},i=1,2,…,n，若Di>θ×D12，则作为第三个聚类中心，c3=vi。

步骤10依此类推，如有k个聚类中心，返回步骤9，计算所有vkap个对象样本到k个聚类中心距离Dik，直到最大最小距离Di不大于θ×D12，结束计算，获得K-means初始聚类中心。

4 实验与结果分析

实验在6个UCI测试公共数据集上进行，数据集分类情况已知。Iris数据集150个样本点为3类、4k2_far数据集400个样本点为4类，Wine数据集178个样本点为3类，ASD_12_2数据集535个样本点为12类，ASD_14_2数据集685个样本点为14类，Leuk72_3k数据集72个样本点为3类。

通过降维图[8-9]显示，可更直观、更真实地展示各种算法获得聚类中心的变化过程。图中用闭合曲线圈出不同的簇，“+”代表聚类中心，并加注文本及簇边框。

利用外部Purity、AC、NMI、JC、RI、FMI有效性指标[10-11]及迭代次数对6个UCI测试公共数据集不同获取初始中心算法的聚类进行评价。

首先以两个数据集Iris数据集，ASD_14_2数据集为例，分别对MMD、AP、APMMD三种算法获得聚类中心的过程及聚类中心优缺点进行描述，并将各方法获得的中心进行K-means聚类，与已知数据集的分类情况用降维图进行对比。图2(a)为已知 Iris分类情况；图2(b)为ASD_14_2已知分类情况。

图2 UCI测试公共数据集已知分类情况

4.1 MMD、AP、APMMD算法获得初始聚类中心点对比

1) MMD算法对Iris数据集获得的初始聚类中心如图3(a)所示：① 簇1、3初始中心点在簇的边界;② 簇1、2、3均获得一个中心，不存在同簇多个中心而导致簇中心的缺失(对比已知图2(a))。MMD算法对ASD_14_2数据集获得初始聚类中心如图3(d)所示：① 初始中心点基本在各簇的边界；② 因簇6、9获得两个中心点，同簇多中心而导致簇7、11缺失中心点(对比已知图2(b))。

2) AP算法对Iris数据集获得6个聚类中心如图3(b)所示：① 大于已知簇数(k=3)；② 簇1、2、3均获得2个聚类中心；③ AP算法中心点具代表性，不在簇的边界；④ 每个簇均获得初始中心，不存在簇中心的缺失(对比已知图2(a))。AP算法对ASD_14_2数据集获得21个聚类中心如图3(e)所示：①大于已知簇数(k=14)；② 其中簇2、3、4、5、6、9、10同簇为2个聚类中心。簇1、7、8、11、12、13、14为1个聚类中心，每个簇均获得初始中心，不存在簇中心的缺失(对比已知图2(b))。

3) APMMD算法：该算法分两步获得K-means初始聚类中心。

(1) 首先用AP算法从原始数据集X={x1,x2,…,xn}获得多个聚类中心作为下一步MMD的候选中心。AP算法对Iris数据集获得6个聚类中心见图3(b)。AP算法对ASD_14_2数据集获得21个聚类中心见图3(e)。

(2) 再用MMD算法从AP获得的候选聚类中心获得 个初始聚类中心。然后MMD算法对AP算法从Iris数据集获得的6个AP候选中心中去掉了同类多出的点，获得3个初始聚类中心图3(c)(APMMD算法聚类中心)，对比已知图2(a)。最后MMD算法对AP算法从ASD_14_2数据集获得的21个AP候选中心中去掉了同类多出的点，获得14个初始聚类中心图3(f) (APMMD算法聚类中心)，对比已知图2(b)。

可以看出，MMD对簇数较小的数据集基本适应，对簇数较大的数据集存在同类多点而导致一些簇的缺失。AP中心簇数大于实际簇数。APMMD算法能较好的为每簇找到一个合理的聚类中心。

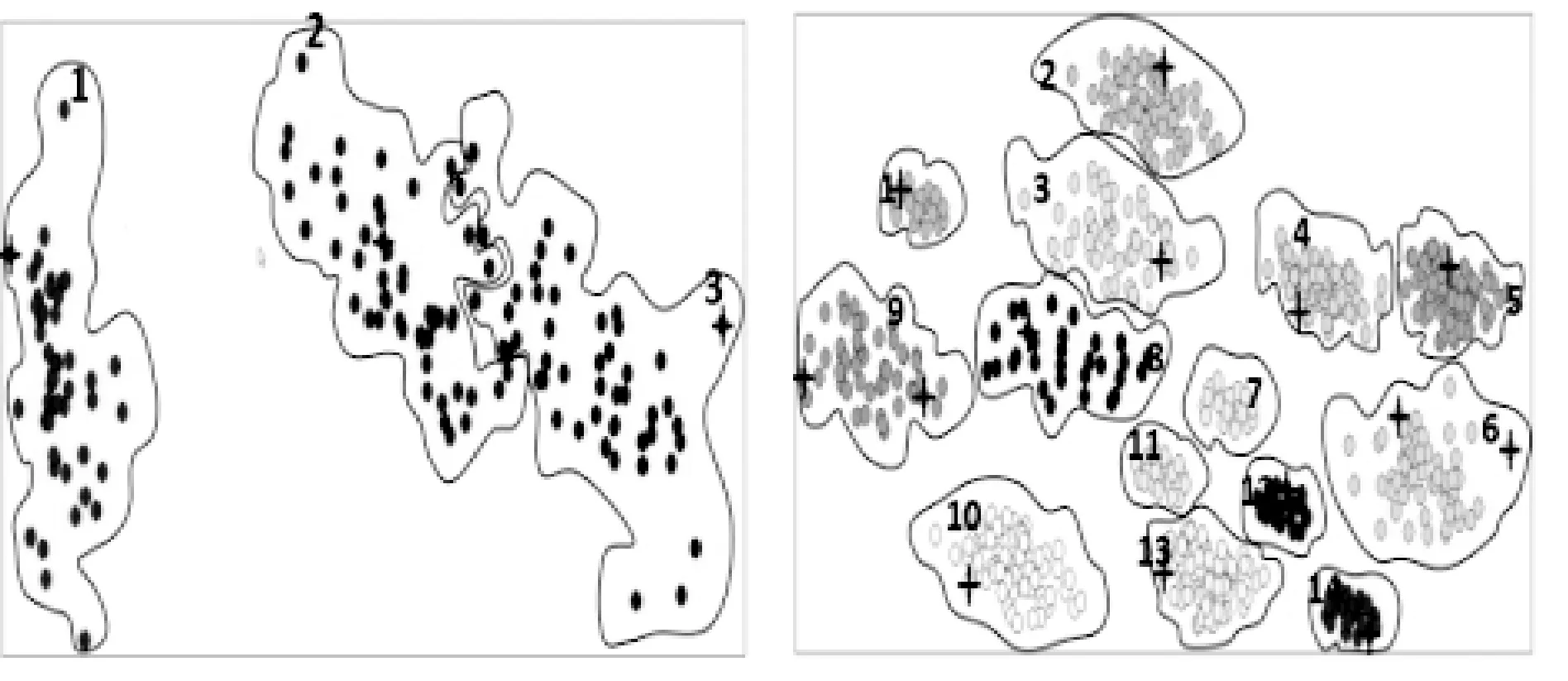
(a) MMD获得Iris的中心 (b) MMD获得ASD_14_2的中心

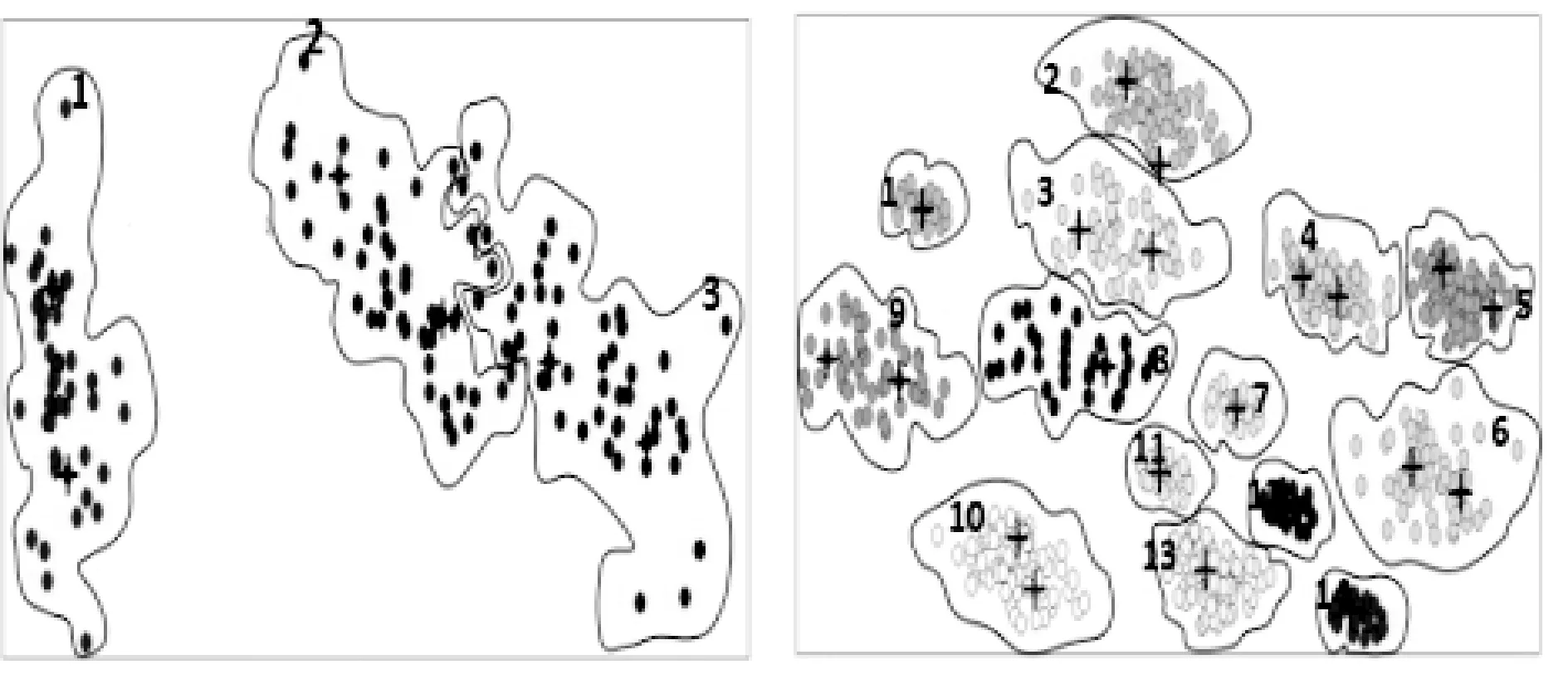
(c) AP获得Iris的中心 (d) AP获得ASD_14_2的中心

(e) APMMD获得Iris的中心 (f) APMMD获得ASD_14_2中心图3 MMD、AP、APMMD算法获得中心点对比

4.2 MMD、AP、APMMD算法对K-means改进聚类结果图对比

(1) MMD对K-means改进的聚类结果。MMD算法对Iris数据集获得的聚类中心，通过K-means聚类迭代，聚类中心最后接近实际中心，聚类结果图4(a)与图2(a)已知分类基本一致。对ASD_14_2数据集获得的聚类中心，通过K-means聚类迭代，部分中心最后接近实际中心，部分将陷入局部最优、且同类多点情况，见图3(d)簇6、9分成了两类。聚类结果图4(d)与图2(b)已知分类相差较大。主要是ASD_14_2聚簇数较大，因MMD算法受K值的限定，求取的聚类中心有同类多点而导致初始类的缺失原因，初始类缺失的图3(d)簇7、11划分给了其他的簇。

(2) AP对K-means改进的聚类结果。AP算法对Iris数据集获得6个聚类中心，大于已知簇数(k=3)，聚类分类结果如图4(c)所示，其与已知图2(a)不符。

AP算法对ASD_14_2数据集获得21个聚类中心，大于已知簇数(k=21)，聚类分类结果如图4(d)所示，其与已知的图2(b)不符。

(3) APMMD对K-means改进的聚类结果。APMMD算法对Iris数据集通过K-means聚类迭代，聚类中心最后接近实际中心，聚类结果如图4(e)所示，其与图2(a)已知分类基本一致。

APMMD算法对ASD_14_2数据集通过K-means迭代，聚类中心全部接近实际中心，聚类结果如图4(f)所示，其与图2(b)已知分类完全一致。

可以看出，MMD、APMMD算法获得的初始聚类中心对簇数较小的Iris数据集基本适应，只是因MMD中心在簇边界，聚类收敛速度要低于APMMD中心。MMD对簇数较大的ASD_14_2数据集存在同类多点而导致一些簇的缺失，聚类结果与已知分类相差较大，说明MMD对簇数较大的数据集不适应。AP算法中心簇数大于实际簇数，自然不能直接应用。APMMD算法能较好地为Iris数据集、ASD_14_2数据集的每个簇找到一个合理的聚类中心，聚类结果自然较好。

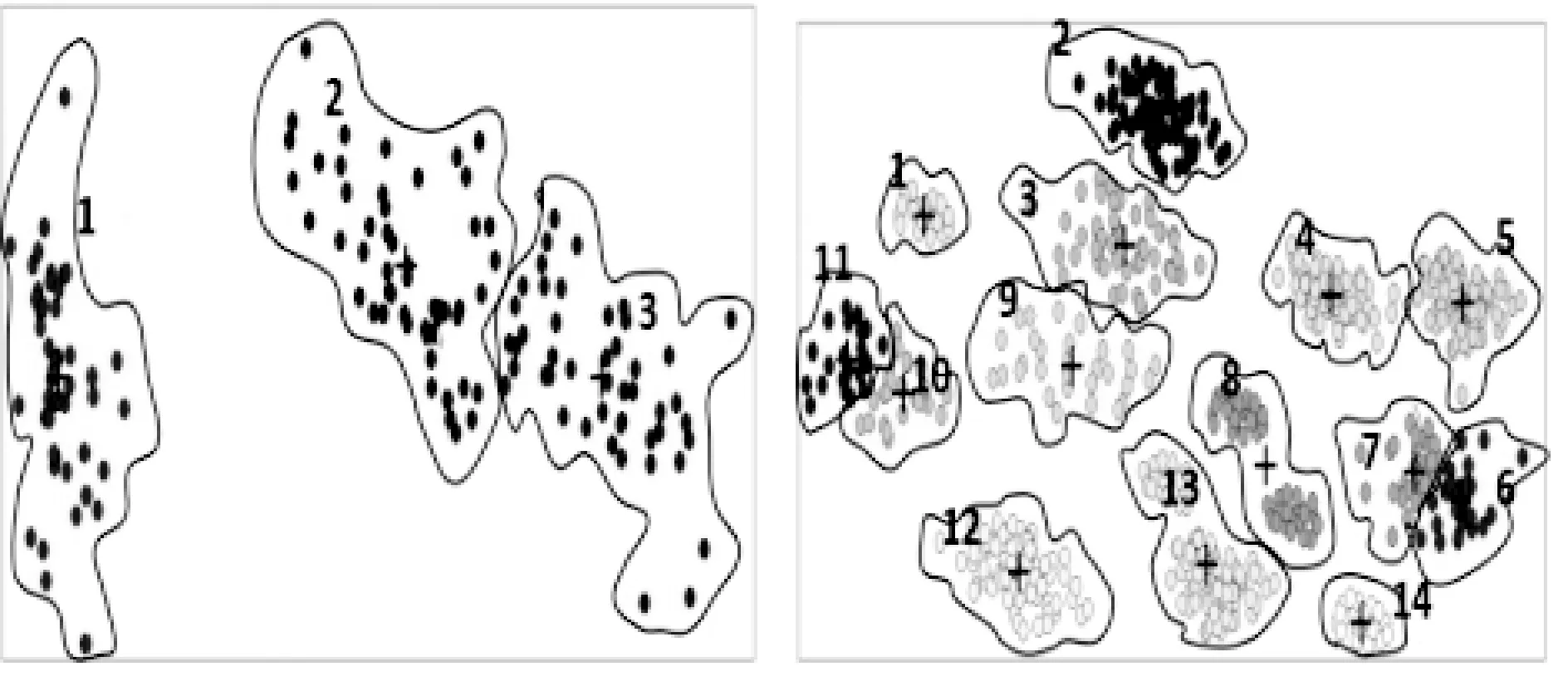
(a) MMD改进Iris聚类 (b) MMD改进ASD_14_2聚类

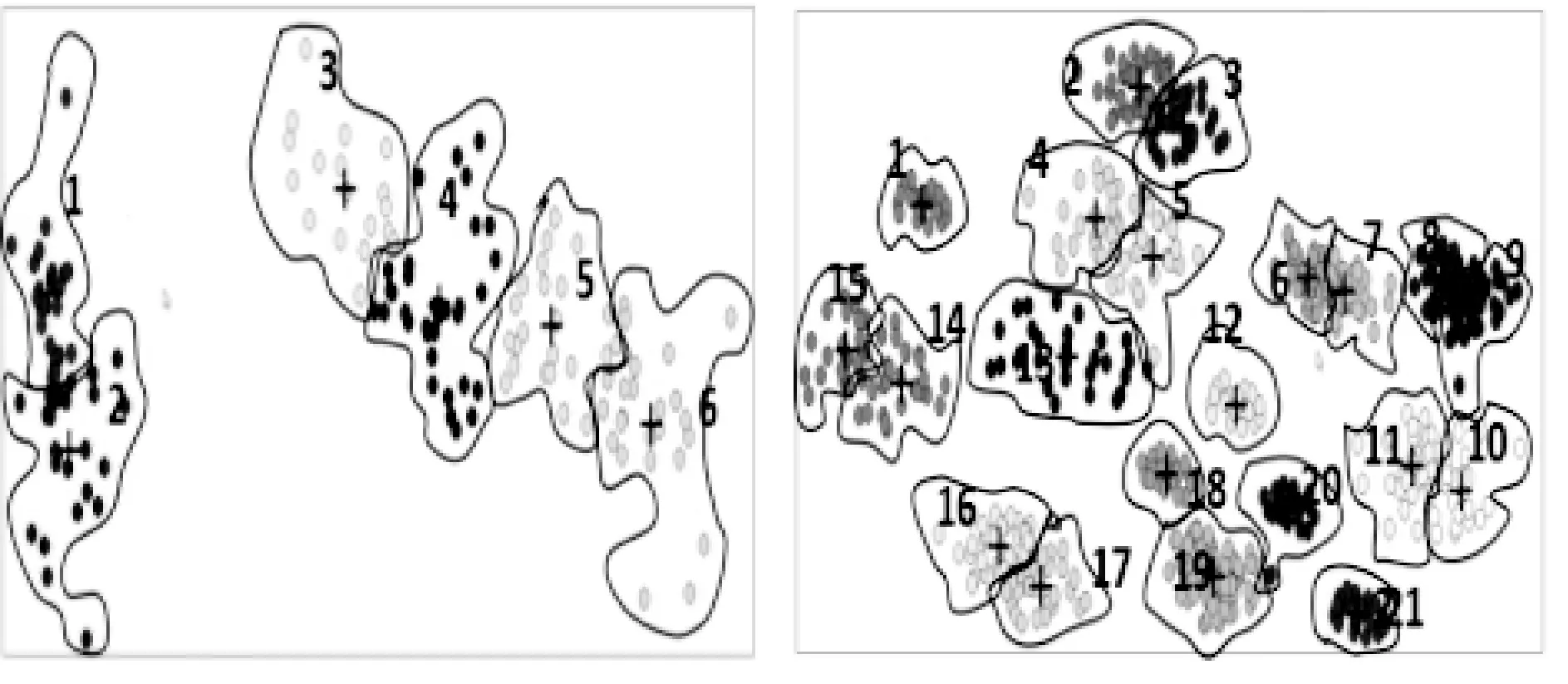
(c) AP改进Iris聚类 (d) AP改进ASD_14_2聚类

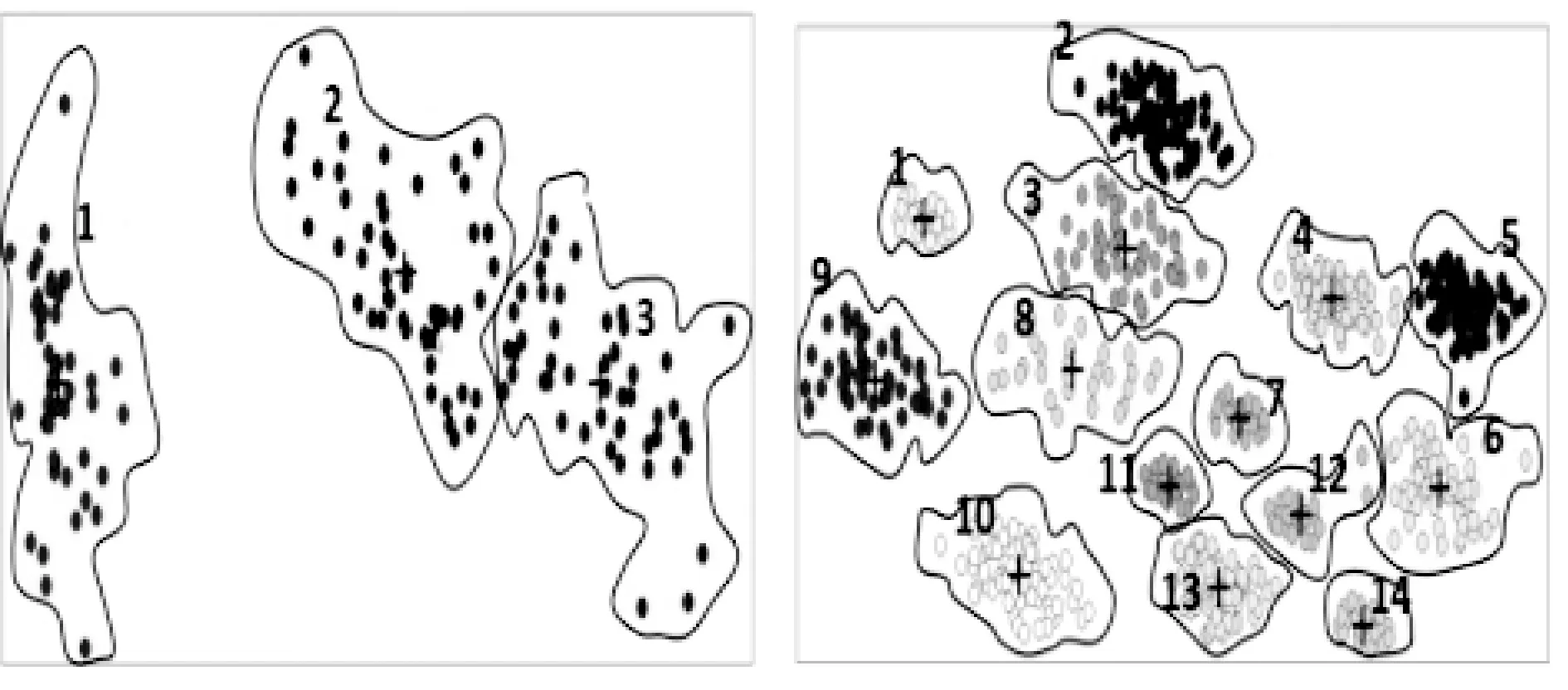
(e) APMMD改进Iris聚类 (f) APMMD改进ASD_14_2聚类图4 MMD、AP、APMMD改进K-means聚类结果对比

4.3 有效性指标对比

聚类的性能指标可评价聚类性能的质量，在聚类方法相同的情况下，可评价K-means初始聚类中心的质量。

聚类的性能指标分为两类：① 外部指标，由聚类结果和某个参考模型进行比较而获得；② 内部指标，由本身的聚类结果而得到，不利用任何参考模型。

最后本文方法将与随机、金字塔、MMD、MMD & SSE和M-AP几种已有改进聚类算法进行比较，采用多个外部指标Purity、AC、NMI、JC、RI和FMI对6个UCI测试公共数据集对几种算法聚类结果进行评价，数据集分类已知。从表1可以看出，随机中心聚类各有效性指标远低于改进算法和APMMD算法的有效性指标。

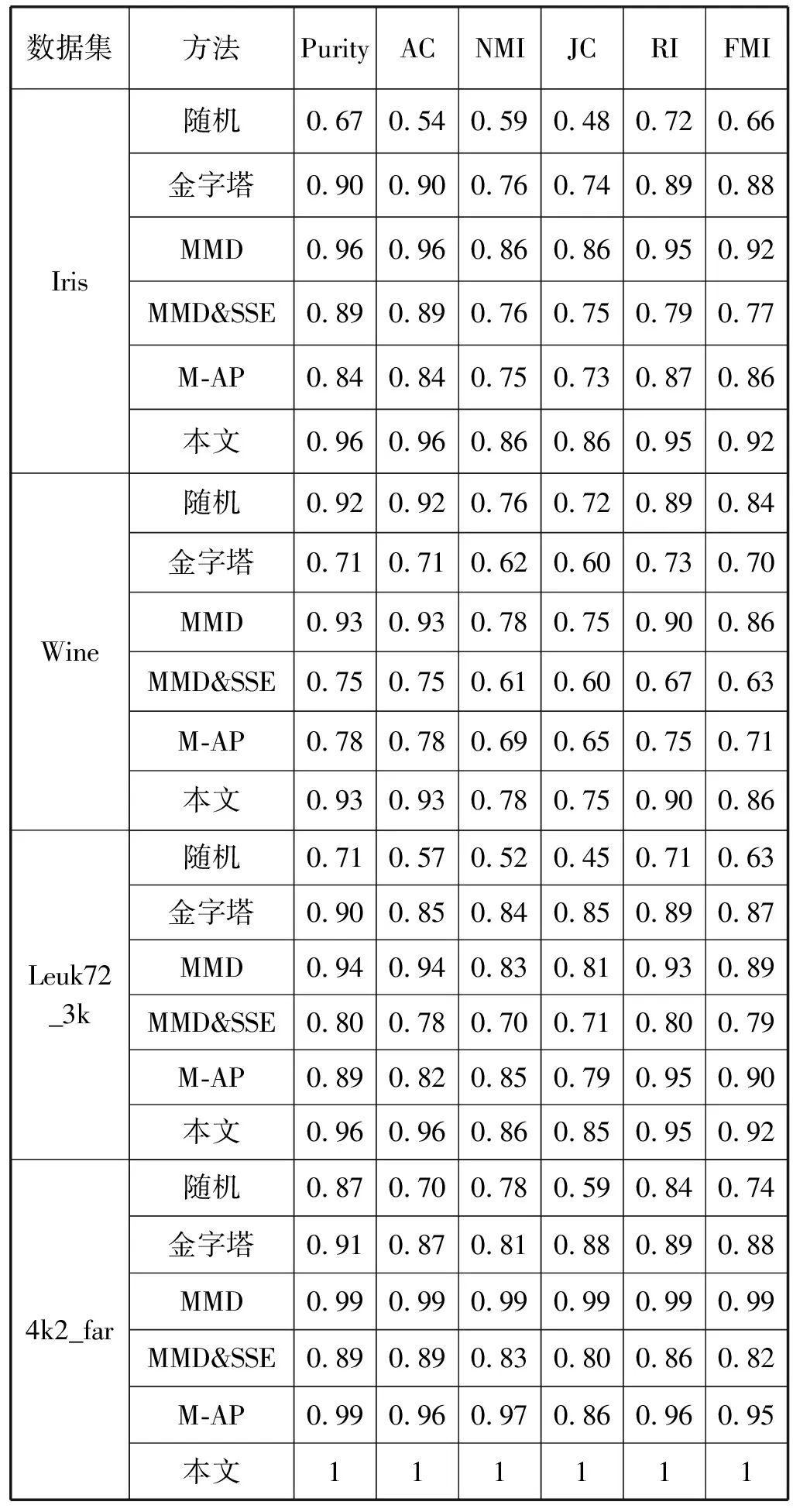
表1 数据集聚类有效性指标对比

续表1

对于Iris、4k2_far、Wine和Leuk72_3k簇数不大的4个数据集，MMD算法和APMMD算法初始聚类中心的聚类指标基本一致。但对于数据集簇数较大的ASD_12_2、ASD_14_2数据集，MMD算法有效性指标全低于APMMD算法。对于4k2_far、ASD_12_2两数据集，APMMD算法的6个有效性指标全为1，正确识别率为100%、对于ASD_14_2数据集，则接近完全吻合。充分说明了改进的APMMD算法求取的初始中心优于随机和其他算法。

4.4 迭代次数对比

在聚类方法相同的情况下，聚类收敛速度也可评价初始聚类中心的质量。用几种算法分别求得6个数据集的初始中心，并依次用于K-means聚类，其收敛迭代次数对比如图5所示，可以看出随机、金字塔、MMD、MMD&SSE、M-AP算法获得的初始聚类中心聚类迭代次数都远大于APMMD算法。因算法初始中心在簇的边界，收敛迭代次数要大于APMMD。

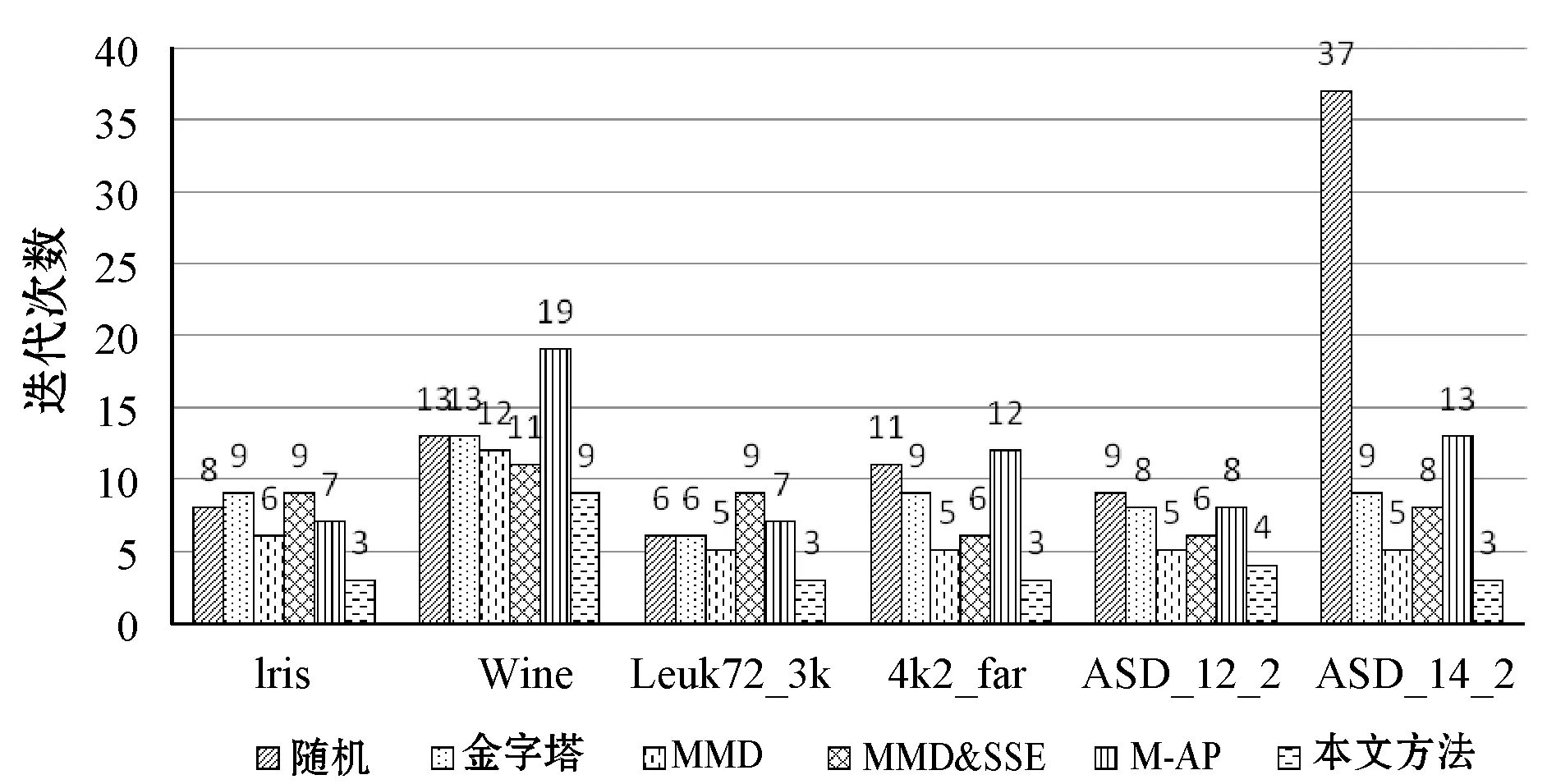
图5 不同初始中心的K-means聚类收敛迭代次数对比

5 结 语

本文通过对经典的K-means算法、MMD算法及AP算法的研究，并进行实验对比、聚类结果质量评价，证明了初始聚类中心的选择对K-means算法的聚类结果有极大的影响，不同的初始聚类中心会有不同的聚类结果，不合理的初始聚类中心可能导致聚类结果的局部最优，且降低聚类算法的收敛速度，影响聚类效果。MMD算法获得的初始聚类中心对簇数较小的数据集基本适应，对簇数较大的数据集存在同类多点而导致一些簇的缺失，聚类精度不高。AP算法获得的聚类中心簇数大于实际簇数，不能直接应用。APMMD算法能较好地为数据集的每个簇找到一个合理的聚类中心，较其他几种算法改进K-means聚类精度更高、迭代次数更少、收敛速度更快。