基于Bi-GRU和自注意力的智能电网虚假数据注入攻击检测

陈 冰 唐永旺

1(河南工业大学漯河工学院 河南 漯河 462000) 2(中国人民解放军战略支援部队信息工程大学信息系统工程学院 河南 郑州 450001)

0 引 言

智能电网以其可靠、高效和经济的传输特点成为现代电力系统最重要的组成部分，然而智能电网严重依赖数据通信和大规模数据处理技术，容易遭到各种恶意网络攻击[1]。尽管已经颁布了很多针对智能电网安全的通信标准、官方指南和监管法律(如IEC 61850-90-5、NISTIR7628等)，恶意网络攻击仍活跃于智能电网中。

虚假数据注入攻击FDIA是Liu[2]等提出的恶意网络攻击技术，被证明是一种对智能电网状态估计产生严重影响的恶意网络攻击行为。其通过规避现有的数据注入监测系统，篡改电网的状态估计数据，诱导电网控制中心做出错误决策，导致整个智能电网出现故障。如何高效地检测 FDIA，对于保障智能电网安全运行具有重要意义。

传统的FDIA检测思路主要归为两种[3-4]。一是策略性地保护部分关键基础测量数据的安全，避免恶意数据注入的发生。如Kim等[5]提出两种快速贪婪算法分别用于选择待保护的测量子集数据和寻找存储安全相量测量单元的位置；Bi等[6]利用图形分析研究方法引入到FDIA检测中，提出精确、低复杂度的近似算法来选择保护系统中最小的数据测量值。二是通过独立检验每个状态变量进行FDIA检测。如Liu等[7]考虑到电网状态时间测量的内在低维度以及FDIA的稀疏性质，将FDIA检测视为低秩矩阵分离问题，并提出核规范最小化和低秩矩阵分解两种优化方法来解决该问题；Ashok等[8]提出了一种在线FDIA检测算法，该算法利用统计信息和状态变量的预测来检测量测异常。

近年来随着智能电网通信数据量级的增加和FDIA方法的不断升级, 传统方法在进行FDIA检测时越来越力不从心。机器学习以及深度学习算法逐渐应用在智能电网恶意网络攻击检测中，并较传统检测方法检测性能有明显提升[9-13]。Ozay等[14]利用监督和半监督机器学习方法完成对高斯分布式攻击的分类。Esmalifalak等[15]设计了一种基于分布式支持向量机的标签数据模型和一种无监督学习的统计异常检测器。He等[16]采用条件深度信念网络有效学习了FDIA的高维时间行为特征。Niu等[17]利用卷积神经网络提取和长短时记忆网络(Long Short Term Memory Network, LSTM)学习量测状态序列的时间和空间关系特征，进而实现FDIA检测。James等[18]基于小波变换和单向门控循环单元(Gated Recurrent Unit，GRU)进行系统的状态连续估计，检测序列状态中的FDIA。Wang等[19]利用3层LSTM作为序列编码器，学习FDIA样本的特征，在测试数据中准确率达90%。深度学习算法可以自动学习电网中各节点的状态量测数据特征，发现异常状态序列或对异常序列分类，整个过程不需要人工设定特征。

然而，现有基于循环神经网络[17-19](Recurrent Neural Network, RNN)的FDIA检测方法在训练量测值时仅使用了多层单向的RNN训练框架，单向的RNN模型在处理序列数据时只能利用已经出现过的序列元素，忽略了未来的序列信息，导致模型性能下降，影响特征最终的提取效果。另外，这些方法中只选取RNN最后一个时刻的隐状态或者各时刻隐状态的拼接作为提取的特征，无法突出注入攻击数据的特征。因为注入攻击向量不一定会对状态量测数据的每一维都均匀地注入攻击，有可能只对一部分维数的数据进行攻击。自注意力机制[20]广泛应用在自然语言处理领域，用于挖掘与当前预测词关系紧密的上下文词语。由此推断可以通过自注意力机制关注量测数据中被注入攻击的位置，从而在提取量测数据特征时对这些位置的隐状态给予更高的权重。

综上所述，在文献[17-19]研究基础上，本文提出一种基于Bi-GRU和自注意力的FDIA检测方法，经查阅文献可知，在FDIA检测领域引入自注意力机制尚属首次。首先将样本数据进行去均值和归一化处理，采用Bi-GRU对量测序列的前向和后向进行建模，输出各时间步的前向和后向隐状态，将前后向隐状态的拼接作为当前元素包含上下文信息的特征。然后利用自注意力机制为被注入攻击的时间步隐状态分配更高的权重，将各隐状态的线性加权和作为样本序列的深层特征表示。最后，将该特征表示输入到全连接神经网络层和Softmax层，输出样本的预测概率，完成FDIA检测。

1 相关背景

1.1 虚假数据注入攻击

在电力系统中，待估计的状态变量包括电压幅值V∈Rn和相位角θ∈([-π,π])n，n是总线数量。令z=[z1,z2,…,zm]T∈Rm表示量测向量，x=[x1,x2,…,x2n]T∈R2n代表状态变量，e=[e1,e2,…,em]T∈Rm代表量测误差向量。在标准直流系统下，可忽略电阻，电压幅值均为1，仅考虑带有相位角的状态变量，量测值和状态变量的关系为：

z=Tx+e

(1)

式中：T是m×n的拓展结构雅可比矩阵。求使加权残差平方和最小的状态估计变量x，目标函数为：

j(x)=(z-Tx)TR-1(z-Tx)

(2)

式中：R是协方差矩阵。利用加权最小二乘法求解式(2)的目标函数：

(3)

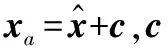
1.2 GRU简介

GRU和LSTM都是RNN的变种，性能在很多任务上不分伯仲，但是GRU少一个控制门，训练参数较少，训练时更容易收敛。因此，本文利用GRU[22]作为编码器的基本组成单元，GRU的输入输出结构如图1所示。

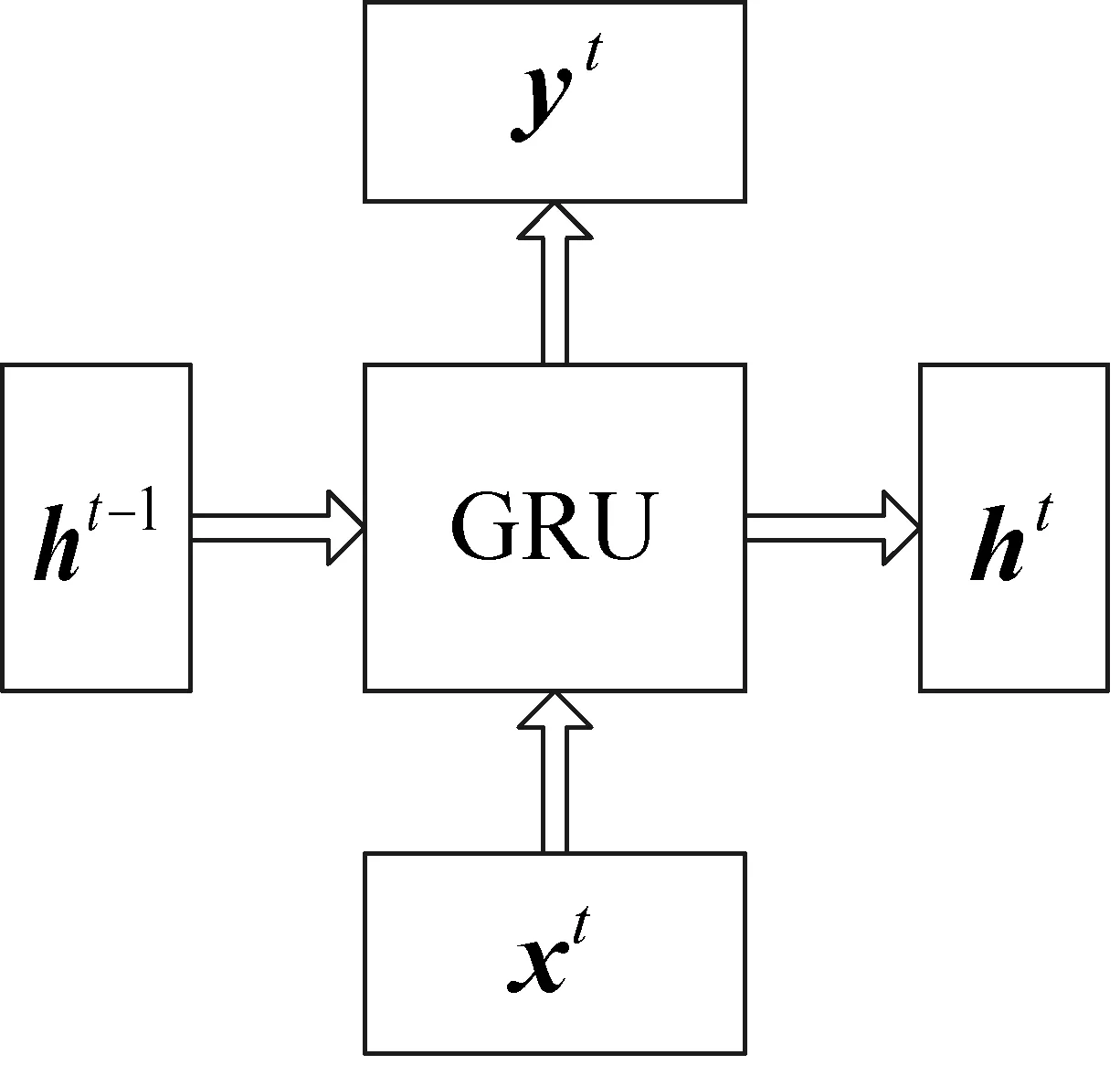
图1 GRU的输入输出结构

图1中，xt为当前输入，ht-1为上一个节点传递的隐状态，其包含之前节点的相关信息。GRU通过xt和ht-1得到当前隐藏节点的输出yt和传递给下一个节点的隐状态ht，其具体工作流程如图2所示。

图2 GRU内部工作原理图

1) 在t时刻，GRU通过ht-1和xt来获取重置门r和更新门z的状态，如下所示：

rt=σ(Wrxt+Urht-1)

(4)

zt=σ(Wzxt+Uzht-1)

(5)

2) 利用重置门“重置”ht-1包含的信息，得到ht-1′=ht-1⊙rt，与xt拼接后，通过tanh激活函数将数据映射到[-1,1]，得到ht′：

ht′=tanh(Wxt+rt⊙Uht-1)

(6)

式中：⊙表示矩阵对应元素相乘。

3) 利用更新门“更新记忆”：

ht=zt⊙ht-1+(1-zt)⊙ht′

(7)

更新门范围取值范围为[0,1]，门控信号越接近1，代表“记忆”下来的数据越多；越接近0则代表“遗忘”的越多。

2 基于Bi-GRU和自注意力的智能电网虚假数据注入攻击检测

本文利用双向GRU 网络结合自注意力机制提取攻击样本的特征, 构建了基于Bi-GRU和自注意力机制的 FDIA 检测模型，其结构如图3所示。

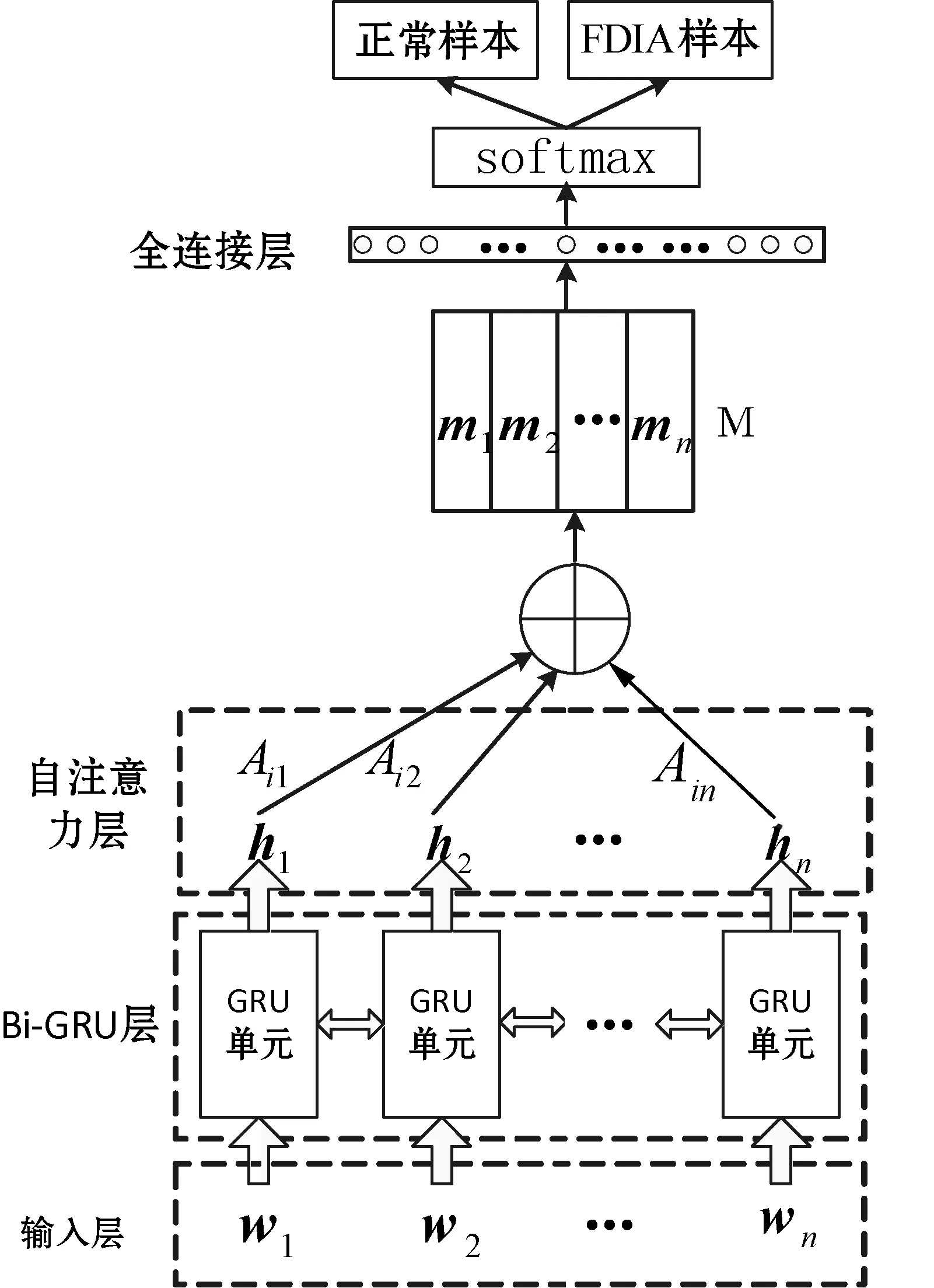
图3 本文提出的FDIA检测模型框架

该模型主要分为Bi-GRU层、自注意力层以及全连接和Softmax层三大部分。

2.1 Bi-GRU层

Bi-GRU由前向GRU和后向GRU组合而成，其具体结构如图4所示。

图4 Bi-GRU训练流程

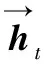
(8)

(9)

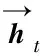
2.2 自注意力层

自注意力层的作用就是在H上施加注意力，具体过程如图5所示。

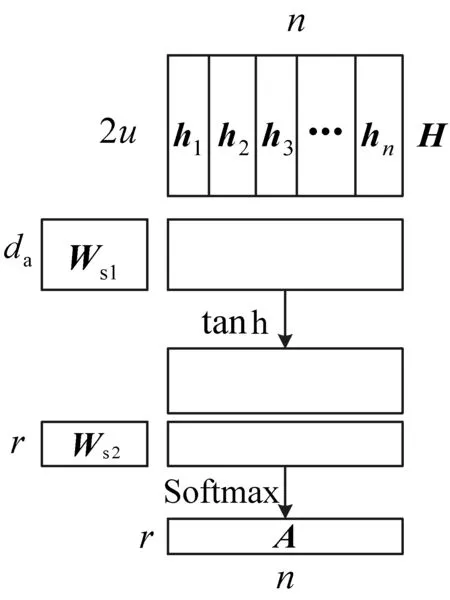
图5 自注意力机制计算示意图

自注意力层将Bi-GRU的隐状态集合H作为输入，输出注意力向量a：

a=Softmax(ws2tanh(Ws1HT))

(10)

式中，Ws1是维数为da×2u的权重矩阵；ws2是维数为da的参数向量；da为一个超参数；a的维数是n。Softmax函数保证输出的注意力向量的每个元素代表一个概率，且所有元素和为1。按照注意力权重分配向量a将H线性加权求和即可得到状态测量序列的嵌入表示m。

然而，一个m通常只关注序列S某些维度的特征，FDIA可以对状态量测序列的多个维度值进行攻击。因为一个m并不能代表序列S的所有攻击特征，所以需要增强注意力，计算多个代表不同维度特征的m作为序列S的嵌入表示。假设需要计算序列r个方面的特征，则ws2的维度扩展为r×da并记作Ws2，a扩展为注意力权重分配矩阵A：

A=Softmax(Ws2tanh(Ws1HT))

(11)

序列S的嵌入表示由m扩展为维数是r×2u的M矩阵：

M=AH

(12)

随后将M输入全连接层和Softmax层，输出识别概率，具体如下所示：

Y=Softmax(WfM+b)

(13)

式中：Wf是全连接层的权重矩阵；b为偏置；Y是Softmax层计算的概率结果。

3 实 验

3.1 实验数据

本文选择该领域主流的IEEE 30-bus和IEEE 14-bus节点测试系统作为测试环境，系统网络拓扑、节点数据、支路参数等均从 Matpower 中获得。在每个环境中利用Matpower软件仿真生成150 000个正常量测数据样本，标签为-1。另外根据现有的FDIA种类[19]构造了50 000个可以绕过传统基于残差不良数据检测的FDIA样本，标签为1。IEEE 30-bus中每个样本包括112个量测值, IEEE 14-bus中每个样本包括54个量测值。每个测试系统的量测值包括电压幅值、总线相位角、总线注入有功功率和无功功率、各支路注入有功功率和无功功率等，将正常样本和FDIA样本进行去均值和归一化处理，分别按照7∶3的比例随机抽取样本制作训练集和测试集。

3.2 评测标准

本文采用准确率、漏报率和误报率三个FDIA检测领域通用的评测指标验证本文方法的可行性和有效性，首先定义以下变量：

真负类(Ture Negative) 表示将正常量测样本正确地识别成正常量测样本的数量, 记为Tn。

假负类(False Negative) 表示将正常量测样本误识别成FDIA样本的数量, 记为Fn。

真正类(Ture Positve) 表示将FDIA样本正确的识别成FDIA样本的数量, 记为Tp。

假正类(False Positive) 表示将FDIA样本误识别成正常量测样本的数量, 记为Fp。

(1) 准确率(记为Ac)计算表达式为：

(14)

式(14)表示所有被正确判断的样本数量占所有样本的百分比。准确率越高，算法越好。

(2) 正报率计算表达式为：

(15)

式(15)表示在所有被检测为FDIA样本中，被正确预测FDIA样本所占的百分比。正报率越高，算法越好。

(3) 误报率计算表达式为：

(16)

式(16)表示在所有被检测为正常样本中，被错误预测样本所占百分比。误报率越高，算法越差。

3.3 实验设置与结果分析

本文选取文献[15]、文献[19]的方法作为对比方法。文献[15]利用标签数据的监督学习训练分布式支持向量机对FDIA样本检测，测试结果记为SVM。文献[19]基于两层单向的LSTM模型学习状态量测值序列的特征，测试结果记为LSTM。同等条件下，将LSTM替换为GRU，测试结果记为GRU。另外，仅利用双向GRU模型学习状态量测值序列的特征，利用该特征检测FDIA样本，测试结果记为Bi-GRU。

本文方法首先分别将两个测试环境的样本进行去均值和归一化处理为112维和54维的序列数据，提高训练速度。使用TensorFlow 深度学习框架构造Bi-GRU和自注意力机制组合的模型结构。根据训练模型的经验，本文采用一个输入层、3个Bi-GRU和自注意力机制组合层、一个全连接层和一个Softmax层的结构。训练IEEE 30-bus量测数据时，每个单向GRU层有112个GRU单元，训练时间步长为112；训练IEEE 14-bus量测数据时，每个单向GRU层有54个GRU单元，训练时间步长为54。GRU单元的隐藏节点数为300，各单元之间共享训练参数，优化算法选取Adam[23]，epochs设置为100，每批数据batch_size大小为256，学习速率为0.01，全连接层的隐藏节点为3 000，使用dropout技术，避免过拟合问题，dropout设置为0.7[24]，在测试集的评测结果记为Bi-GRU-SA。

实验硬件配置为Intel Xeon E5-2650，128 GB内存的服务器，配备12 GB的双GTX 1080Ti独立显卡进行加速训练。

1) 综合对比实验 本文方法和各对比方法测试结果如表1-表2所示。

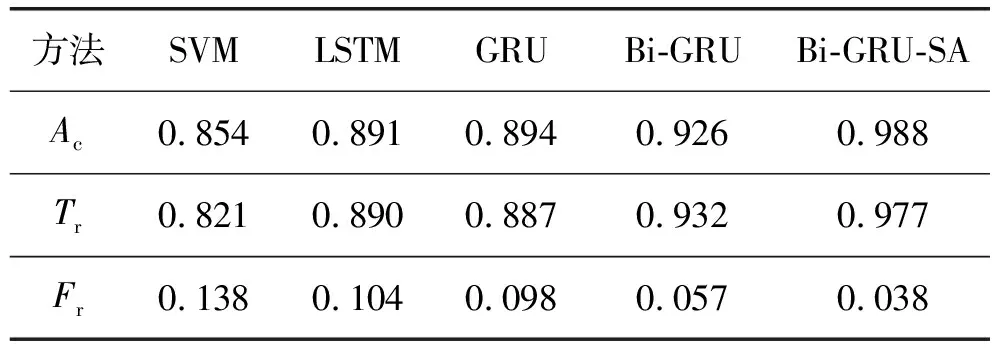
表1 IEEE 30-bus综合实验结果

表2 IEEE 14-bus综合实验结果

从表1和表2可以看出：LSTM和GRU的测试结果优于SVM，这是因为RNN网络在处理高维度序列数据方面比SVM更有优势。GRU和LSTM作为RNN的变种，三项评测指标差别不大。Bi-GRU在计算时刻t的隐状态时可以综合利用量测序列前向t-1时刻和后向t+1时刻的隐状态，而单向的LSTM和GRU仅利用t-1时刻的隐状态，无法准确预测当前时刻的隐状态，因此Bi-GRU三项的评测指标优于LSTM和GRU。在Bi-GRU的基础上加入自注意力层，计算每个时刻隐状态的注意力分配值，将注意力着重放在被虚假数据注入攻击的隐状态，进而利用各时刻隐状态的加权求和得出样本最终的嵌入表示，该嵌入表示可以更加准确地代表量测样本。Bi-GRU-SA的测试结果与对比方法相比有较显著的提升；与次优结果相比，准确率平均提升7.1%，正报率平均提升3.95%，误报率平均降低38.85%。

2) 自注意力提升参数r的分析 注意力提升是自注意力机制的关键一步，因此需要分析r对FDIA检测的影响。以IEEE 30-bus为例，令r在[0,40]内取值，以5为步长训练FDIA检测模型，在测试集进行检测任务，以评测指标准确率分析，结果如图6所示。

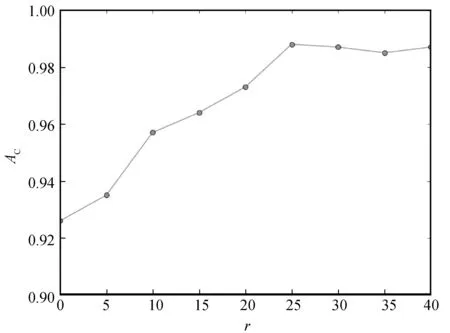
图6 准确率随着r的变化分析

由图6可以看出，在[0,25]的区间内，Ac随着r的增加而增加，从FDIA样本提取的特征也越来越全面，说明注意力提升对检测性能有重要作用。当r在[25,40]之间时，Ac趋于平稳，且当r为25时达到峰值，说明对于本文实验数据来说，25个矩阵m足以代表FDIA样本的特征。

4 结 语

本文提出一种基于Bi-GRU和自注意力机制的FDIA检测方法，解决了当前基于单向多层RNN的FDIA检测方法中无法综合利用序列上下文隐状态的问题。另外，本文首次将自注意力机制引入FDIA样本的特征提取中，以各时间步隐状态的注意力加权和作为样本的嵌入表示，通过注意力的提升准确地计算出样本的深层特征表示，提升了FDIA检测性能。GRU的结构特性决定其只能顺序训练序列的元素，在大规模的数据量下训练模型和利用模型检测均需要消耗大量的时间，如何构造一种可以并行训练序列元素的网络结构是下一步研究的重点方向。