基于扩展FEAST的大规模特征值求解问题研究

李玲玲 李 华

(河南城建学院数理学院 河南 平顶山 467036)

0 引 言

非线性特征值问题[1](Nonlinear Eigenvalue Pro-blems,NLEVP)是计算科学的热门研究课题。其矩阵值函数的有用性，都将受到问题求解难度的限制，伴随着一些特有难题，例如其特征向量通常并不构成n维向量空间的基础，且矩阵值函数的特定形式会影响到求解方法的效率。然而，非线性特征值问题与线性特征值问题有着相同的核心难题：在n的数值较小时有效的求解方法并不一定能很好地扩展到高维问题[2]。此类问题通常侧重于寻找少量特定的、有重要物理学意义的“特征值-特征向量”对。

大部分求解此类高维问题的方法需要生成一个与期望特征对足够接近的初始猜测，以确保收敛性。同时，需要使用能够计算特征值接近的连续特征对，但不会向同一个特征对反复收敛的方法[3]。尤其在期望得到大量特征对的情况下，以上问题更加难以解决。NLEVP算法进一步加大了计算大量特征对的难度，导致不能很好地适应在子空间内求解的降维后的特征值问题。而求解非线性特征值问题所需的计算量至少与求解单个线性特征值问题相等。因此，保持较小的维数至关重要，以确保能够适应较大规模的问题。

围道积分法是解决上述难题的一类算法[4-5]。围道积分法利用柯西积分公式，从而仅计算其特征值位于复平面的用户定义特定区域中的特征对。这样就不需要计算初始猜测，并对维数为n的原始问题中距离很近的特征值进行了分离。此外，围道积分法支持大量特征对的高效并行计算，通过将复平面中的感兴趣区域分割为不相交的子区域，在每个子区域中独立求解特征值，且与其他子区域的特征值无关。

而线性FEAST算法[6-7]是求解线性特征值问题的围道积分法样例。该算法能够求解大规模广义线性特征值问题，具有较好的鲁棒性和优秀的并行可扩展性。本文对线性FEAST算法进行推广，使其能够求解非线性特征值问题，并通过求解一些物理模型问题来解释该算法的特性。

1 非线性特征值问题

给定一个非空的开集D⊆C和一个矩阵值函数T:D→Cn×n，考虑一个非线性特征值问题：找到标量λ∈D和非零向量x∈Cn、y∈Cn，使得：

T(λ)x=0 且y·T(λ)=0

(1)

本文将(λ,x,y)称为T的特征三元组，(λ,x)或(λ,y)均被称为特征对。对于T(λ)=λI-A和T(λ)=λB-A，通过式(1)分别将其简化为标准特征值问题Ax=λx和广义特征值问题Ax=λBx。广义非线性特征值问题的特性与线性特征值问题有着很大的不同，例如T(即使是正则值，即det(T(λ))≠0)可能有无穷多个特征值，属于不同特征值的特征向量不一定是线性无关的，且一个孤立特征值的代数重数虽然是有限的，但不受问题大小n的限制[8]。所有这些特性，使得广义非线性特征值问题非常难以求解。关于该问题更详细的描述，可参考二次特征值问题的相关文献或广义非线性特征值问题[9]。

为便于讨论，本文侧重于研究方阵类多项式特征值问题。找到标量λ∈D⊂C和非零向量x,y∈Cn，以使得：

P(λ)x=0y·P(λ)=0

(2)

式中：P(λ)为n×n的矩阵多项式。

(3)

若P为正则，即det(P)≠0，则式(2)有r个有限特征值(det(P)=0的根)和kn-r个无限特征值(复特征值)。通过线性化，可知k次的n×n矩阵多项式P(λ)有着kn个特征值(有限或无限)，最多kn个右相关特征向量，及最多kn个左相关特征向量。

2 扩展FEAST算法

2.1 FEAST算法

原始FEAST算法被用于求解广义特征值问题，即T(λ)=λB-A，其是一个子空间迭代方法，使用Rayleigh-Ritz投影和近似光谱投影器作为滤波器。FEAST计算与位于复平面中用户定义的特定区域中的特征值相对应的特征对。因此，该算法可被用于并行计算大量特征对，其中将复平面分割为不相交的区域集合，并独立求解每个区域中的特征对(与其他区域中的特征对无关)。

FEAST首先将任意随机初始子空间X(0)投影到感兴趣特征向量所覆盖的子空间来选择感兴趣的特征向量和特征值，然后使用Rayleigh-Ritz程序[10]在该子空间中提取特征值/特征向量的近似。通过使用复围道积分来完成向感兴趣子空间的投影：

(4)

式中：Q为新的投影子空间，在包围着感兴趣特征值的围道中完成积分。若精确完成积分，则滤波器ρ(A,B)成为光谱投影器，ρ(A,B)=XYHB，其中X和Y分别是与感兴趣特征值(即位于闭合曲线内的特征值)相关的精确的右特征向量矩阵和左特征向量矩阵。然而在实践中，无法在式(4)中精确完成积分，因此使用求积规则对其进行逼近。则FEAST算法实际生成的子空间为：

(5)

式中：zj和wj分别为积分节点和权值，通过求解线性系统(zjB-A)Qj=BX(0)来完成求和。由于每个线性系统均独立于其他系统，因此可以并行地同时求解。FEAST通过反复应用求和，将得到的子空间Q正交化，并将其用于Rayleigh-Ritz程序中，对感兴趣特征向量的估计进行迭代式改进。

本文旨在利用FEAST框架的优点来求解NLEVP,使用围道积分对固定维数的子空间进行迭代优化，以求解特征值位于复平面的用户定义区域中的特征对。

2.2 NLFEAST算法

线性FEAST算法可以解释为在复平面上使用多个移位的平移-逆迭代的推广。利用相似的推理，假定非线性FEAST(NLFEAST)算法是使用多个移位的非线性移位-逆迭代的推广：

x(i+1)=T(z)-1T′(λ(i))x(i)

(6)

式中：x(i)和λ(i)为特征向量和特征值在迭代i处的估计;T′(·)为T(·)的导数;z为复平面中位于感兴趣特征值附近的移位。由此预期非线性FEAST围道积分(单个向量)将类似于：

(7)

积分围道包围着感兴趣特征值。但在实践中，式(7)中的更新程序未能向正确的特征值-特征向量对收敛。这是因为在式(7)中使用恒定移位z会造成非线性逆迭代向错误的解收敛。

原始FEAST算法可以解释为移位-逆迭代的推广，使用围道积分以高效地同时使用多个移位。而非线性FEAST算法则可以解释为残差逆迭代的推广，使用围道积分以高效地同时使用多个移位。本文给出了非线性FEAST算法的算法框架，如算法1所示。

算法1T(λ)x=0时的NLFEAST算法

步骤1设子空间Q=X(0)，对Q的列向量进行正交归一化。

步骤2求解投影后的非线性特征值问题:

QHT(λ)Qy=0

(8)

以得到近似特征对(λ,Qy)。

Λ=diag(λ1,λ2,…,λm0)X=[Qy1,Qy2,…,Qym0]

(9)

步骤5通过执行数值积分对搜索子空间进行更新：

(10)

使用求积规则并求解线性系统：

(11)

步骤6对新的搜索子空间Q的列向量进行正交归一化(例如使用QR分解)，并回到步骤2。

非线性FEAST算法中Rayleigh-Ritz步骤与线性算法中的工作原理相同：将残差函数T(λ)投影到子空间Q上，然后选择合适的方法(本文使用了简单线性化)对维数降低后的非线性特征值问题进行求解。得到的Ritz值及Ritz向量被用作期望特征对的新估计。

用于Rayleigh-Ritz程序的子空间，即通过执行围道积分所生成的子空间，应该是正交归一化的(如使用QR分解)。正交归一化能够防止期望特征向量的范数出现发散，并防止Rayleigh-Ritz程序生成伪特征对(即与全尺寸特征值问题的任意特征对均不对应的Ritz对)，由此提升了FEAST迭代的数值稳定性。

在m0=1和nc=1的情况下，算法1大致等价于残差逆迭代。这两种算法的区别在于非线性特征值和特征向量的估计方式不同，以及步骤5中更新向量的缩放差别。算法1通过求解步骤2中的投影非线性特征值问题来计算近似特征向量和近似特征值，而残差逆迭代则使用步骤5中的子空间更新程序对近似特征向量进行更新。

3 数值分析实验

将本文的NLFEAST算法在3个有实践意义的多项式特征值问题上做数值分析实验。

3.1 样例1：非过阻尼质点弹簧系统

考虑一个与质点弹簧系统[11]相关的自共轭(Hermitian)二次特征值问题：

T(λ)x=(λ2A2+λA1+A0)x=0

(12)

式中:

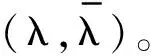
参照文献[12]，首先分析非过阻尼系统。本文设n=1 000，并选择τ=0.620 2，k=0.480 7。图1展示了Q的所有特征值。要考虑计算的特征向量的特征值没有虚部；质点弹簧系统原运动公式的解的指数增长或衰减是这些特征向量的线性组合。

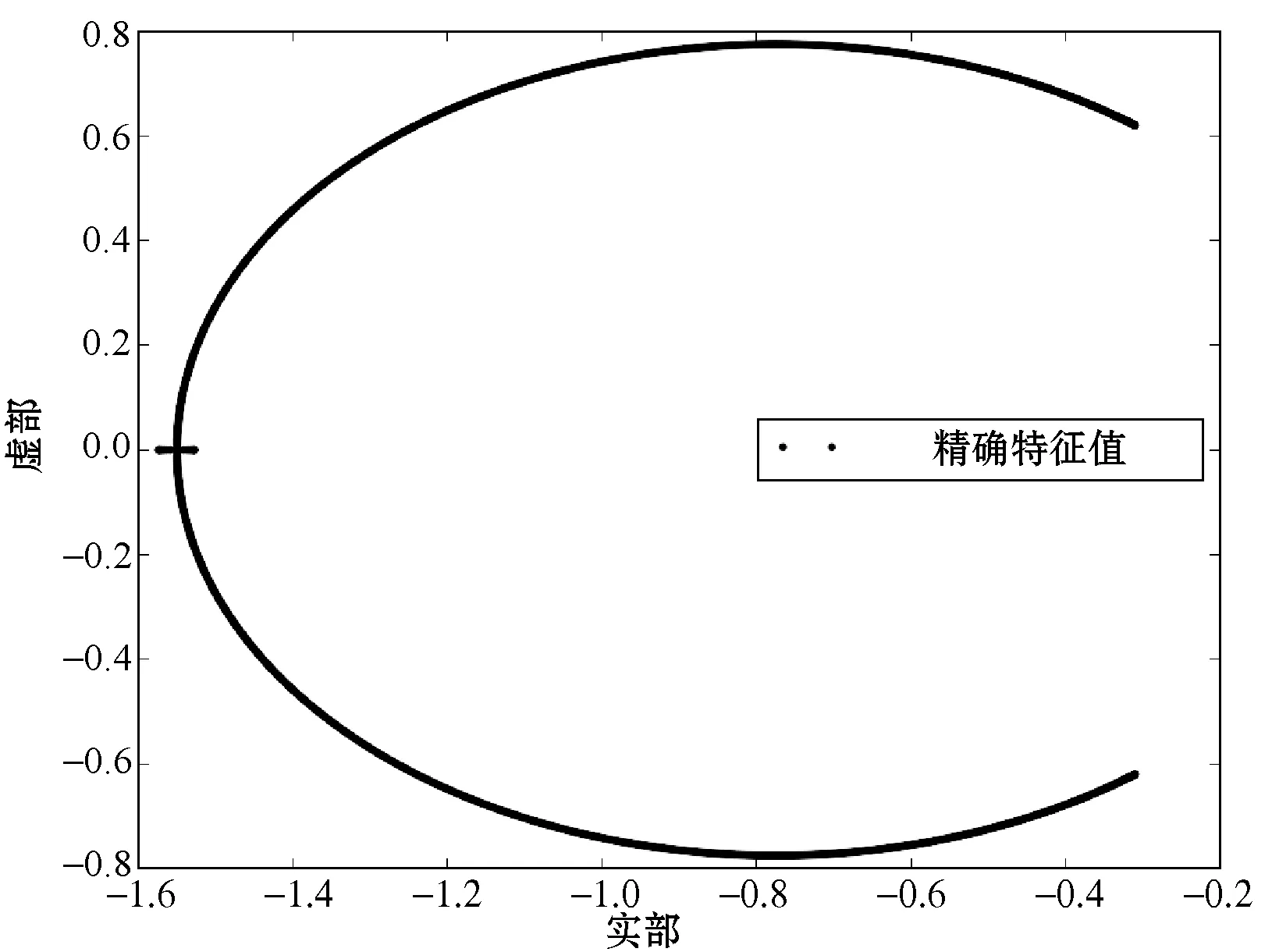
图1 非过阻尼质点弹簧系统的所有特征值

使用算法1中的非线性FEAST方法，计算这20个实特征值的近似。选择的围道为一个椭圆，其中心为区间(-1.6,-1.5)的中点，使用nc=16个求积节点，实轴方向的半径ra=0.05，虚轴方向的半径rb=0.003 5，残值的收敛标准为tol=10-10。在维数m0=22的子空间中，非线性FEAST算法在三次迭代中找到了区间内的全部m=20个特征值。表1给出了使用线性化方法和非线性FEAST算法得到的特征值近似。为完备性起见，本文还列举了所有的最终残值，即‖ri‖2=‖T(λi)xi‖2。

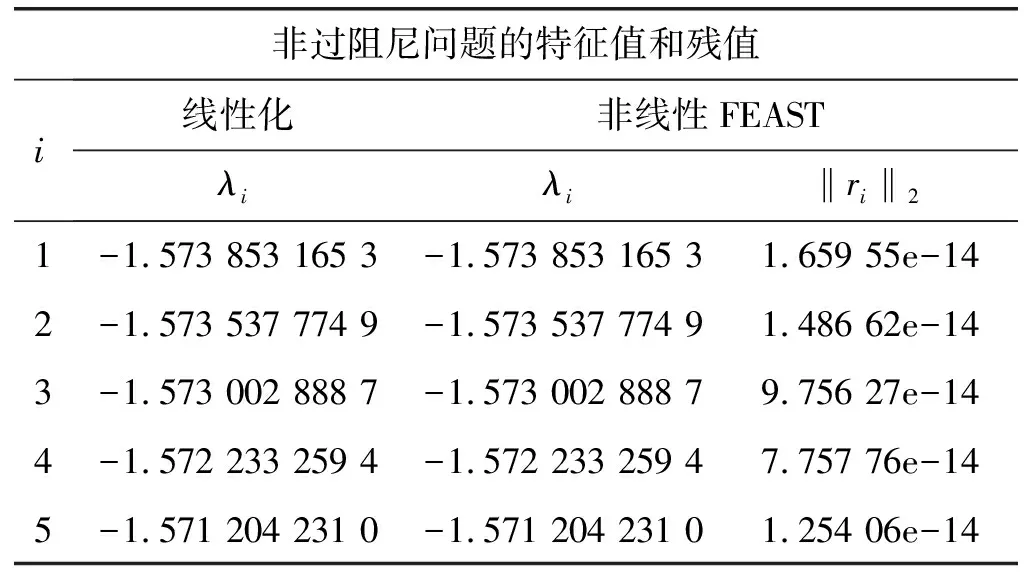
表1 非过阻尼质点弹簧系统在的所有实特征值列表

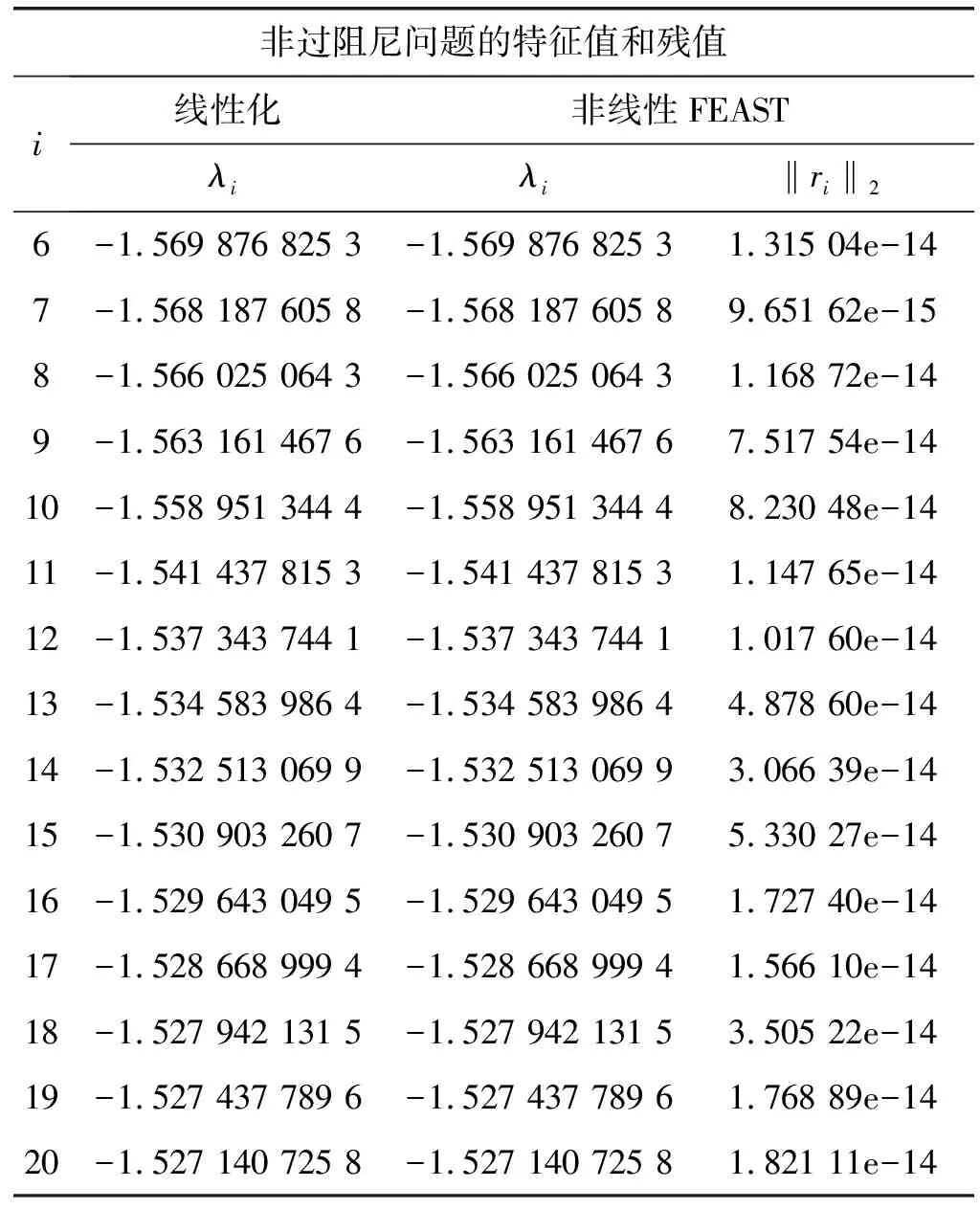
续表1

表2给出了当搜索区间(a,b)增大时，收敛所需的非线性FEAST迭代次数。当求积节点nc的数量保持在16个不变时，扩大搜索区间的影响等同于将求积节点放置在远离感兴趣特征值的地方，由此使得围道积分的准确度降低。区间大小的适度变化仅会造成收敛所需的工作量稍微上升；而区间大小的较大变化往往会要求非线性FEAST迭代次数随之按比例增加。实践中，与期望特征值分布相关的搜索区间的大小而造成的性能降低，可以通过简单地使用大量求积节点而缓解，这种情况下需要更多的并行处理能力来同时求解更多的线性系统。

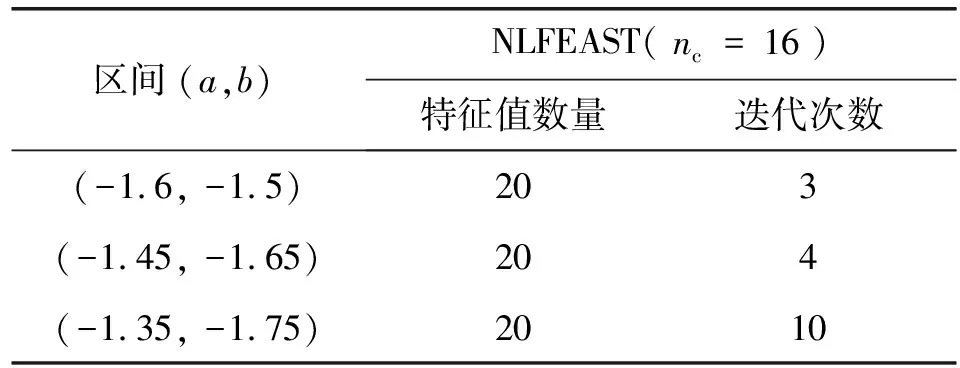
表2 非过阻尼质点弹簧系统的特征值数量

3.2 样例2：一维散射共振

非线性特征值问题的另一个应用是开边界量子透射问题。在开边界量子投射问题中，需要计算量子势的准束缚态，其中粒子可以进入或离开系统，最好不要对外部源进行显式建模。这可以通过求解非线性特征值问题来实现。考虑一个开边界量子透射问题的样例，即一维散射共振问题，其中包含以下紧支有限二乘模型：

(13)

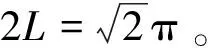
在n=302个点的网格上的有限元离散化得到大小为302的带散射共振的二次特征值，其特征值结果如图2所示。可以看出，r=15.5为半径的圆内共计22个复散射共振。非线性FEAST使用nc=16个求积节点，求解子空间维数m0=30、V0=10的散射共振问题。4次迭代计算这22个散射共振的近似值(收敛容差10-10)，其结果如图3所示。

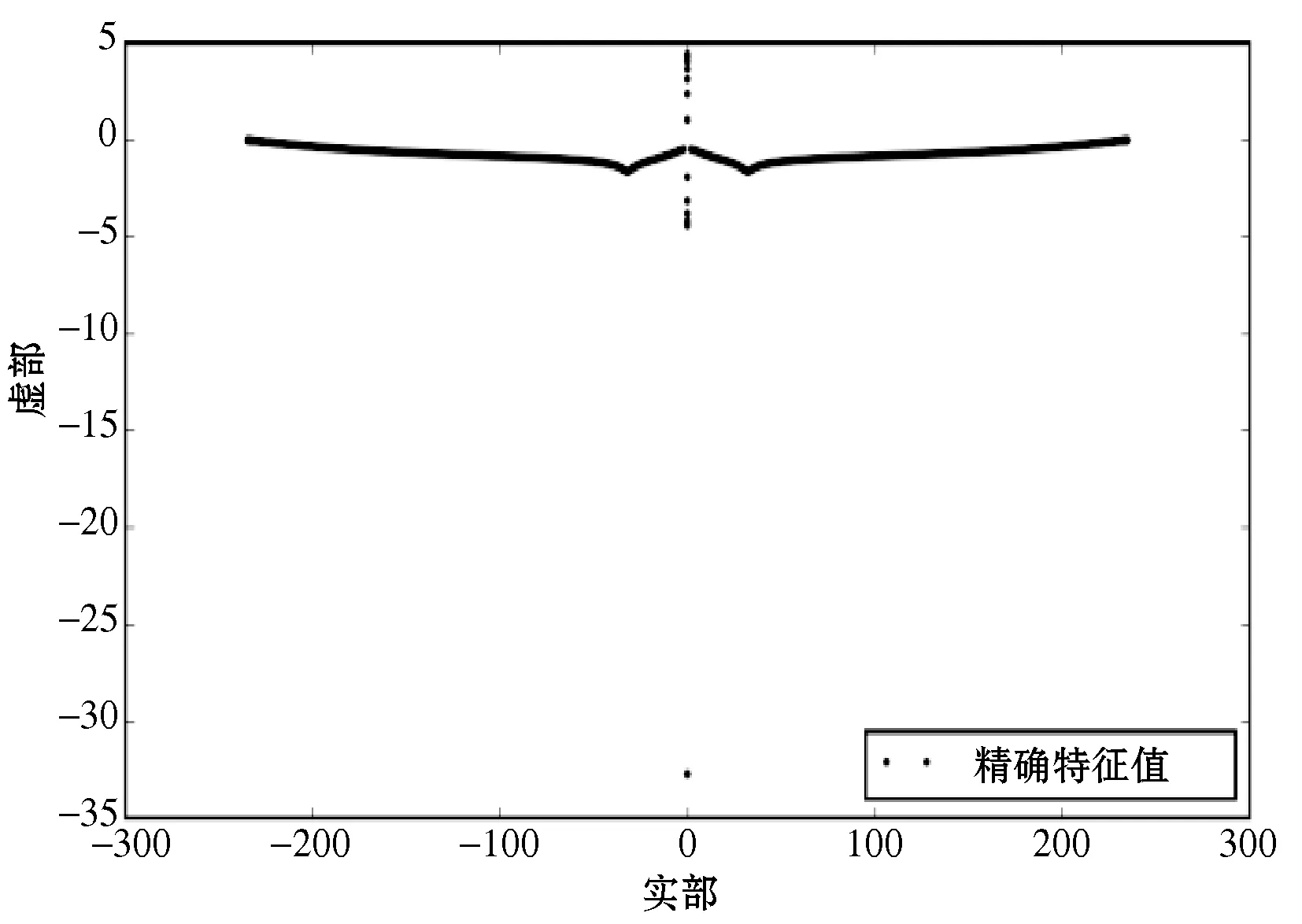
图2 散射共振的所有特征值

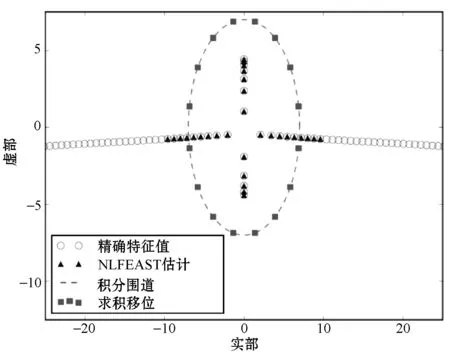
图3 一维散射共振的NLFEAST算法特征值估计

3.3 样例3：轨道振动

较长轨道的振动可建模为以下形式的二次特征值问题[13]：

T(λ)=λ2I+λ(I+A2)+A2+A+I

(14)

式中：A为一个n×n的转换矩阵。对于任意维数n，通过求解以下二次方程给出式(14)的二次特征值问题的特征值：

(15)

式中：μk=-4sin2((k-1)π/n)(1≤k≤n)为矩阵A的特征值，特征值以复共轭对的形式出现。

考虑A的维数为n=50 000，使用NLFEAST算法计算与区间[-7.119 2,-6.965 0]内的特征值相对应的250个特征向量，其中圆形围道的圆心坐标为(-7.042，0)，半径0.077 1。图4展示了其特征值位置和积分围道。

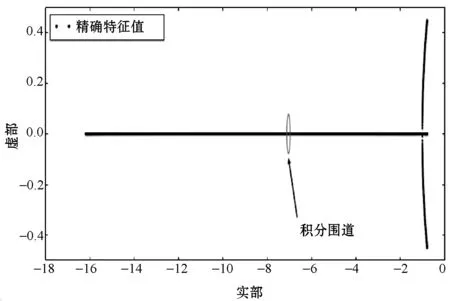
图4 轨道振动特征图示

为进一步比较，本文还使用Beyn法利用相同的积分围道计算相同的250个特征值。表3给出了Beyn法在使用不同的子空间维数和各种数量的求积节点时，与积分围道内的特征值相对应的特征向量的最终特征向量残值。与NLFEAST算法一样，仅考虑残值低于10-2的特征向量为正确特征向量，由此排除伪特征值。

表3 使用Beyn法计算特征值时的向量残值

表3的结果表明，Beyn法和NLFEAST算法在计算一个解时需要的计算量大致相当。例如，当m0=500，nc=8时，NLFEAST算法需要6次迭代以收敛至约10-11，即总计500×8×6=24 000个线性系统解;Beyn法在m0=500时需要nc=64个求积节点以收敛至残差10-12的特征向量，即对应于500×8×8=28 500个线性系统解。

以上两种方法的差异源于计算方式的不同。Beyn法理论上可以并行求解所有相关的线性系统，而NLFEAST算法则可以并行求解最多m0×nc个线性系统。Beyn法的并行性较高，但需要计算更多数量的矩阵分解。在上述案例中，Beyn法需要64次矩阵分解，而NLFEAST算法仅需8次。

4 结 语

本文提出了线性FEAST特征值算法的一个扩展算法，以求解非线性特征值问题。提出的NLFEAST算法使用与线性FEAST算法相同的一系列运算，但修改了围道积分，支持在求解非线性特征值问题时使用固定移位集合和固定子空间维数。线性FEAST算法可被解释为移位和逆迭代的使用多次移位的推广，而NLFEAST算法则可被解释为残差逆迭代的使用多次移位的推广。本文改进数值围道积分提升了近似特征向量子空间的维数，从而系统地提高了算法的收敛速度。