无证书签密的通用可组合机制
王琳杰 田有亮
1(铜仁学院大数据学院 贵州 铜仁 554300) 2(贵州大学计算机科学与技术学院 贵州 贵阳550025) 3(贵州省公共大数据重点实验室(贵州大学) 贵州 贵阳 550025)
0 引 言
签密概念是Zheng[1]于1997年在17届国际密码学年会上首次提出,此概念实现了在一个逻辑步骤内同时完成对消息的签名和加密。与“先签名后加密”的传统方式相比,其在计算和通信方面的开销大幅降低,是实现信息安全传输的一种比较理想的方法。因此,该概念一经提出就引起各国密码学研究者的注意,并迅速成为密码学界研究的热点。在密码学中,对信息的保密和认证一直是该学科研究的重点,而签密却能很好地实现上述两个要求,并且在实际的应用中有着较好的计算和通信开销,因此基于各种密码体制下的签密方案被提出[2-3]。
在传统公钥加密体制中,大多数通信方案都基于证书来实现,而证书则是参与通信各方的身份标志(Identity document,ID),它们都保存在一个称为可信中心(CA)的机构里面。如果想要与网络中某人通信就要到CA中查找相应人员的ID,但是在实际的运行中发现有不可信的CA进行伪造或者修改过期ID的操作,为此密码界的学者想方设法解决不可信CA的问题。1984年,Shamir[4]在基于身份的公钥加密体制方案中提出了一个密钥管理问题,而AL-Riyami等[5]为了解决上述密钥管理问题,于2003年首次提出一种无证书的公钥密码体制,其中用户的私钥是由用户在KGC生成的主密钥的基础上随机选取秘密值生成的,由此克服了传统公钥密码体制中密钥托管问题。
2008年Barreto等[6]首次提出无证书签密(Certificateless signcryption,CLSC)的概念和形式化的定义,随后国内学者提出了很多无证书签密方案[7-14]。文献[12]为了提高运算效率提出了一种使用指数运算的无证书签密方案,方案的机密性和不可否认性是基于计算性Diffie-Hellman(CDH)和离散对数问题。文献[15]基于非配对的广义双线性Diffie-Hellman(NGBDH)问题和Many Diffie-Hellman(MDH)问题提出了基于双线性对的无证书签密方案,方案在标准模型下证明了安全性。同样,文献[16]在随机预言模型下证明了基于双线性对的无证书签密方案的安全性。除此之外,文献[6-10]是基于双线性映射提出的无证书签密方案,而文献[11-14]是基于不适用双线性映射的无证书签密方案。上述文献研究的安全性证明要么是基于IND游戏进行证明,要么是在随机预言机模型下进行证明,要么是在IND游戏和随机预言机模型的结合下进行证明,这些协议的安全性证明只考虑其自身运行时的安全性,并没有考虑与其他协议同时并行运行的情况。当上述协议在作为一个系统的某个子协议或者一个比较复杂的协议的一个部分时,不一定仍能保证其自身的安全性。上述文献没有在通用可组合框架下研究无证书签密方案安全性,因此本文在通用可组合框架下重新定义无证书签密方案的安全性,以达到多协议协同运作环境下的无证书签密方案的安全需求。
通用可组合框架[17](UC framework)是由Canetti提出,其最优秀的性质是模块化设计思想,即该框架中被证明安全的协议之间进行并行运行时,仍能保证协议是安全的[18]。由于该框架具有协议之间进行并行运行的优秀性质,因此在此框架下许多密码协议的安全性被重新研究,例如文献[18-24]在UC框架下研究了门限签名协议、多重数字签名协议、代理重签名协议、群组通信协议、安全多方计算协议、群签名、自认证盲签名协议、分散电子投票协议,及基于身份的代理签密协议等。
本文在UC框架下研究了无证书签密协议问题,提出一种无证书的签密机制。首先,本文定义了无证书签名协议πCLSC;其次,在UC框架下定义了无证书签密对应的理想函数FCLSC;最后证明了该协议πCLSC安全实现理想函数FCLSC的充要条件是协议πCLSC满足在适应性选择密文攻击下的不可区分性。本文的贡献如下:(1) 提出了通用可组合框架下无证书签密协议模型,并设计了无证书签密的理想函数FCLSC;(2) 构造了一个安全实现理想函数FCLSC的无证书签密协议πCLSC;(3) 基于理想函数FCLSC和离散对数问题给出一个具体的协议实例。
1 准备知识
1.1 UC框架
UC框架由现实模型、理想模型、混合模型三个模型构建而成。现实模型描述协议的真实运行情况,由现实协议π、环境Z、现实的敌手A之间的交互构成。理想模型描述协议执行的理想情况,由一个不可攻陷的理想函数F(它通过一组“可信中心”的指令来获取所需的功能或规范)、虚拟参与者(Dummy parties)及理想攻击者S组成,并利用F来保证协议的安全性。其中,参与者之间以及敌手S与参与者之间不直接通信;所有参与者和敌手S均与理想函数交互。在理想模型中,虚拟参与者将自己的输入交给F,由F计算后将结果返回给参与者。如果现实模型中的协议可以访问理想模型的某个理想函数,那么这个模型就是混合模型。如果协议π能访问理想函数F,称其为F-混合协议。
UC框架中,由于存在“仿真”使得现实模型可以访问理想模型中的理想函数,从而将现实模型的安全规约到理想模型的安全。协议仿真的概念将环境视为在和敌手A运行协议π的进程与和敌手S运行协议φ的进程之间的“交互识别”。如果从任何环境的角度来看,对于协议π仿真协议φ,如果没有环境可以判断它是否与π和一些(已知的)敌手或与φ和其他一些敌手进行交互,那么协议π与φ一样好。令REALπ,A,Z(k,z)和IDEALF,S,Z(k,z)表示现实模型和理想模型下环境机Z的输出,其中k是安全参数,z是环境机Z的输入。
定义1[21]两个二元概率分布集合X和Y是不可区分的,记作X≈Y,如果对于任何c,d∈N存在k0∈N,对于所有k>k0和所有z∈Uκ≤kd{0,1}κ有:
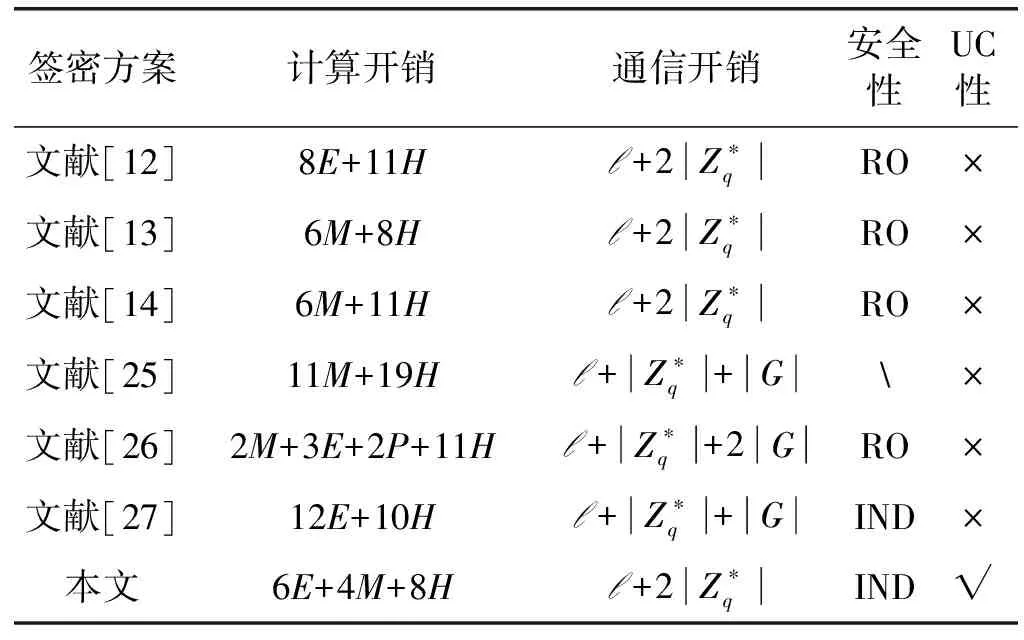
|Pr(X(k,z)=1)-Pr(Y(k,z)=1)| 定义2[21]如果对于任何现实攻击者A,都存在一个理想攻击者S,对于任何环境机Z,等式REALπ,A,Z(k,z)≈IDEALF,S,Z(k,z)恒成立,则称协议πUC-实现了理想函数F,也称协议π是UC安全的。即在k是安全参数且z是环境机Z的输入的情况下,Z与A和π的各方运行交互之后输出1的概率同Z与S和F交互之后输出1的概率的不同可以忽略不计。 定理1[21]设π是F-混合协议,协议ρUC-实现理想函数F,则协议πρ/FUC-仿真协议π。 定义3[12]一个无证书的签密方案是由系统初始化、部分密钥生成、私钥生成、签密算法和解签密算法五个多项式时间算法组成。该方案的合法参与者有签密者P、签密消息接受者R和密钥生成中心PKG。 1) 系统初始化(Setup):PKG输入安全参数1λ,生成输出主密钥s和系统参数params,保密s,公开params。 2) 部分密钥生成(PartialKey.Extract):PKG将需要产生部分密钥的用户P的身份IDp、params和s输入,输出P的部分私钥PSp和部分公钥PPp。 3) 私钥生成(PrivateKey.Extract):用户P将params、IDp、PSp和随机选取的秘密值sp输入,输出用户私钥SKp及公钥PKp。 4) 签密算法(SignCrypt):签密者P输入params、待签密消息m、签密者的IDp及其私钥SKp和接受者身份IDr及其公钥PKr,输出密文σ。 FCLSC和签密者P、接收者R、密钥生成中心PKG及敌手A一起运行过程执行如下。 1)Setup:当收到PKG消息(Setup,sid)后,发送(Setup,sid,PKG)给敌手A;当从A收到(Setup,sid,PKs),输出(Setup,sid,PKs)给PKG,记录(PKG,PKs)。 2)PartialKey.Extract:当从P收到第一个消息(PartialKey.Extract,sid),验证sid是否等于(P,sid′),则发送(PartialKey.Extract,sid,IDp)发送给敌手A。将从A收到的(PartialKey.Received,sid,PKG,IDp)转发给用户P。 3)PrivateKey.Extract:当收到用户P的签名密钥生成请求(PrivateKey.Extract,sid)时,将(PrivateKey.Extract,sid,IDp)发给A。当从A收到(PrivateKey.Received,sid,PKG,IDp,up,vp)时(vp是一个确定性多项式算法的描述,up是一个非确定性多项式算法的描述),记录(P,up,vp)并输出(PrivateKey.Received,sid,IDp,vp)给用户P。 4)SignCrypt:当收到签名者P发送的签密请求(SignCrypt,sid,IDp,IDr,m),验证sid的有效性,并检查(P,up)是否已经记录。如果被记录,则向R输出错误并停机;否则将(SignCrypt,sid,IDp,IDr)发给A,并计算σ=vp(m),记录(m,σ,up),输出(Ciphertext,sid,IDp,IDr,σ)给R。 定义4如果对于任何多项式时间的敌手,能够以一个可忽略的概率赢得以下游戏,则称一个无证书签密方案在适应性选择密文攻击下具有不可区分性(IND-CCA2)。 IND-CCA2游戏是由攻击者A和挑战者B共同完成。 1) 挑战者B选取安全参数λ进行系统初始化Setup,将系统参数params给攻击者A。 2) 初始化。攻击者A执行下述操作: (1)PartialKey.Extract询问:攻击者A选择一个身份IDv给挑战者B,B计算PartialKey.Extract(params,s,IDv)→(PSv,PPv),并发给A; (2)PrivateKey.Extract询问:攻击者A选择一个身份IDv和秘密值sv给挑战者B,B计算PrivateKey.Extract(params,IDv,PSv,sv)→SKv,并发送给A。 3) 训练阶段Ⅰ。 (1)SignCrypt询问:攻击者A选择两个身份IDv、IDr和消息m,挑战者B对IDv进行私钥生成询问,对IDr进行公钥生成询问,计算σ=SignCrypt(SKv,PKr,m)并将σ发给A。 (2)UnSignCrypt询问:攻击者A选择两个身份IDv、IDr和密文σ,挑战者B对IDr进行私钥生成询问,对IDv进行公钥生成询问,计算m′=UnSignCrypt(PKv,SKr,σ)并将此结果发给A。 4) 挑战。攻击者A输出两个长度相同的消息m0、m1及两个挑战身份IDv、IDr,其中IDr不能在之前的初始化和训练阶段出现过,挑战者B随机选择i∈{0,1},计算σ=SignCrypt(SKv,PKr,mi)并将结果发给A。 5) 训练阶段Ⅱ。过程与训练阶段Ⅰ一样,执行多项式有界次询问,但是不能对IDr执行前面初始化和训练阶段的各种询问。另外,不能对挑战中的签密σ进行UnSignCrypt询问。 (6) 猜测。攻击者A输出一个数值i′,如果i′=i,则攻击者A攻击成功,即赢得游戏。 UC框架下的无证书签密协议由五个算法组成,即πCLSC=(Setup,PartialKey.Extract,PrivateKey.Extract,SignCrypt,UnsignCrypt),协议的执行步骤如下: 1) 收到输入(Setup,PKG,sid)后,PKG运行Setup(1λ)→(params,s),输出相应的参数params。 2) 收到输入(PartialKey.Extract,sid)后,PKG先验证sid=(sid′,PKG),再运行PartialKey.Extract(params,s,IDp)→(PSp,PPp),输出(Partial.Received,sid,IDp)。 3) 收到输入(Partial.Received,sid,IDp)后,P运行PrivateKey.Extract(params,IDp,PSp,sp)→SKp。算法vp是签密算法SignCrypt(SKp,·),算法up是验证算法UnSignCrypt(PKp,·)。P输出(PrivateKey.Received,sid,IDp,vp)。如果P从敌手A处得到一个“corruption”的请求,把签名算法vp(·)输出给敌手A。 4) 收到输入(SignCrypt,sid,IDp,IDr,m)后,发送方P运行签密算法σ=vp(m),输出(Ciphertext,sid,IDp,IDr,σ)。 5) 收到输入(UnSignCrypt,sid,m,IDp,IDr,σ,up)后,验证者计算f=UnSignCrypt(PKp,m,σ),并输出(UnSignCrypt,sid,m,IDp,IDr,σ,f)。 为了证明协议πCLSC在UC框架下可实现理想函数FCLSC,本文在理想模型中构造一个理想的敌手,使得环境不能区分是现实模型中的执行还是理想模型中的执行。 定理2设CLSC是无证书的签密方案,协议πCLSC安全实现理想函数FCLSC,当且仅当CLSC是IND-CCA2安全的。 必要性证明:假设协议πCLSC安全实现了理想函数FCLSC,那么对于任何环境Z都不可能区分它是在与理想协议FCLSC和理想环境中的敌手即仿真敌手S交互还是在与现实协议πCLSC和现实环境中的敌手A交互。因此CLSC满足IND-CCA2安全性,即没有敌手能够以不可忽略的概率赢得IND-CCA2游戏。 首先构造与理想函数FCLSC交互的理想敌手S,S执行如下的操作:模拟理想函数FCLSC及模拟与环境的通信。 (1) 系统初始化:在收到FCLSC的消息(Setup,sid,PKG)后,运行参数生成算法Setup(1λ)→(params,s),并返回相应的(params,PKs)。 (2) 部分密钥生成:在收到FCLSC的消息(PartialKey.Extact,sid,PKG,IDp)后,运行部分密钥生成算法PartialKey.Extract(params,s,IDp)→(PSp,PPp),产生(PSp,PPp),返回PPp。 (3) 私钥生成:在收到FCLSC的消息(PrivateKey.Extract,sid,IDp)后,运行私钥生成算法Private.Extract(params,IDp,PSp,sp)→SKp,产生SKp,返回PKp。 (4) 签密:在收到FCLSC的消息(SignCrypt,sid,IDp,IDr)后,如果消息发送者P未腐败,则返回SignCrypt(paramas,m,IDp,IDr,SKp,PKr)→σ,并记录(m,σ);否则接收(SignCrypt,sid,m),并返回(SignCrypt,sid,m,σ)。 (5) 解签密:在收到FCLSC的消息(UnSignCrypt,sid,σ)后,返回UnSignCrypt(params,σ,IDs,IDr,SKr,PKs)→m,发送(m,f=0)给所有参与方;否则,将(m,f=1)发送给参与方。 下面证明仿真敌手S模拟了敌手A,构造游戏IND-CCA2中的敌手A′: 挑战者B产生系统参数params后,激活敌手A′。 ① 在收到A′输入(Setup,sid)后,B输出sid=(sid,params)回应。 ② 在收到A′输入(PartialKey.Extract,sid)后,(PartialKey.Extract,sid)请求时,B输出(PSp,PPp)回应。 ③ 在收到A′输入(PrivateKey.Extract,sid,IDv)后,向B发出(PrivateKey.Extract,sid,IDp)请求时,B输出(SKp,PKp)回应。 ④ 在收到A′输入(SignCrypt,sid,IDp,IDr,m)后,向B发出(SignCrypt,sid,m)请求时,B运行SignCrypt(sid,IDp,IDr,m),并返回σ。 ⑤ 在收到A′输入(UnSignCrypt,sid,m,IDp,IDr,σ)后,运行UnSignCrypt(params,m,σ)→f并返回f。当f=1时,签密成功;否则是伪造消息的签密或者是由敌手来决定签密是否有效。 根据上述对理想敌手S的描述,可以看出,在理想模型在执行时,对于伪造签名的验证结果总是输出0,因为不存在(sid,m,*,up,1);而现实模型在执行时,如果伪造签密是成功的,则输出的结果是1。 充分性证明:反证法。 假设CLSC是IND-CCA2的,那么协议πCLSC不能安全实现理想函数FCLSC,即环境机Z能区分它是与理想环境下的FCLSC和S交互还是与现实环境下的πCLSC和D(Dummy adversary)交互。用环境机Z构造一个敌手B伪造出有效无证书签密。 与敌手B进行如下交互:B可以调用环境机Z。 ① 当Z用输入(Setup,sid)激活参与者P,如果P是“corrupted”,将结果(params,s)返回给Z。 ② 当Z用输入(PartialKey.Extract,sid)激活参与方P,B将结果(PSp,PPp)返回给P。如果P是“corrupted”,则将(PSp,PPp)返回给Z。 ③ 当Z用输入(SetSecret.Value,sid)激活参与方P,将结果(sp,PKp)返回给Z。 ④ 当Z用输入(PrivateKey.Extract,sid,IDp)激活参与方P,B将结果(SKp,vp)返回给P。如果P是“corrupted”,B将结果(SKp,vp)返回给Z。 ⑤ 当Z用输入(SignCrypt,sid,IDp,IDr,m)激活发送方P,B将得到的签名σ返回给P。 ⑥ 当Z用输入(UnSignCrypt,sid,m,IDp,IDr,σ,up)激活参与者P时,B令f=UnSignCrypt(PKp,m,σ),输出(UnSignCrypt,sid,m,σ,f)给P。 敌手B成功的概率分析如下:如果环境机Z是在与现实环境中的协议πCLSC和敌手A交互,因为签密σ是有效的,所以Z将输出1;如果环境机Z是在与理想模型中的理想函数FCLSC和模拟敌手S交互,因为不存在(sid,m,*,up,1)所以对于伪造签密的验证结果Z总是输出0。证毕。 3) 私钥生成。当收到(PrivateKey.Extract,sid,IDi),IDi计算公钥PKi=(Xi,Yi),私钥为SKi=(xi,yi)。 表1 开销的对比 注:√表示方案具有该属性,×表示方案不具有该属性。 可以看出,文献[12-14]的计算开销与本文方案的差不多,而文献[25-27]计算开销就比本文方案大得多,但是文献中的方案都不具有通用可组合性;在通信开销方面本文方案和文献[10-12]的相同,文献[25-27]方案的消息长度较大,导致通信中的传输开销比较大。与现有的无证书签密方案相比,本文方案在计算开销和通信效率方面都有一定的优势;另外,由于本文方案具有通用可组合性,与任意一组协议组成安全协议或者是作为任意系统的一个组成部分使用时,也能保证安全。 本文研究了无证书签密方案的通用可组合安全性,给出了无证书签密的形式化定义,定义了无证书签密方案的理想函数,设计了满足UC安全性的无证书签密协议,证明了通用可组合的无证书签密协议安全性与IND-CCA2安全性之间的等价关系,并基于离散对数问题给出了一个具体的通用可组合的无证书签密实例。1.2 无证书签密协议
2 无证书签密的理想函数FCLSC

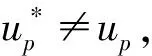
3 无证书签密协议的安全模型
3.1 基于IND-CCA2的安全性
3.2 UC框架下的无证书签密协议πCLSC
4 协议的安全性分析
5 实例及性能分析
5.1 协议实例
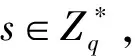
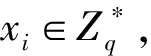
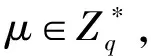
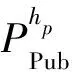
5.2 性能分析
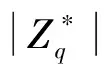
6 结 语

