CMOS密勒补偿三级放大器建立时间的最优设计
蒋新淼,郭裕顺
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
0 引 言
随着工艺技术的进步,器件的特征尺寸不断降低。在低电压下,通常采用多级级联结构来设计高增益运放。多级运放需采用更为复杂的补偿结构,如嵌入式密勒补偿(Nested Miller Compensation,NMC)、反向嵌入式密勒补偿(Reversed Nested Miller Compensation,RNMC)等,以满足稳定性等要求[1-3]。而对于开关电容电路、A/D转换器等离散或混合信号系统,往往还需要使多级运放的建立时间满足性能指标的要求。因此,关于多级运放建立时间最优或最小化的设计研究逐渐受到人们关注。Pugliese等[4]针对三级NMC运放,提出了一种通过开环传递函数阻尼因子进行补偿电容计算,实现建立时间最小化的设计方法,但分析过程中忽略了零点的影响。随后,又通过对一般三阶系统的完整分析,改进了确定补偿电容大小的方法[5],并将其推广至具有不同补偿方案的多种三级运放设计[6]。文献[7]提出一种基于开环传递函数中阻尼因子控制的类似方法。文献[8-9]运用数值优化技术,在最小化三级运放建立时间的同时,考虑了噪声性能的优化。文献[10]利用贝塞尔滤波器的特性来确定运放传递函数中的相关系数,再进行建立时间的设计。这些运放建立时间的最小化设计方法均是基于运放的三阶传递函数的,而三阶传递函数是忽略了运放小信号等效电路中各种寄生元件后的近似,因此获得的结果也是近似的,无法达到真正的建立时间最优设计。为此,本文提出一种基于运放建立时间最小化条件方程求解的设计方法。由于求解过程中的计算均采用了SPICE仿真,考虑了各种寄生元件的影响,可得到准确的电路级设计结果。
1 基于传递函数的建立时间最小化设计
采用NMC补偿的CMOS三级运放如图1所示,其简化的小信号等效电路如图2所示,其中Gmi(i=1,2,3)是各放大级的跨导,Ri,Coi分别是各级的输出电阻与电容,Cc1,Cc2是两个补偿电容。由图2等效电路可知,其电压传递函数是一个三阶的有理函数。运放建立时间一般由运放在单位反馈下的阶跃响应定义。将图2连成单位反馈闭环,其传递函数表示为[5]:
(1)
式中,s是复频率,p1,ωn,ζ(0<ζ<1)分别是运放闭环的主极点、除掉主极点后两阶系统的自然频率和阻尼系数,z1,z2,A0是2个零点和直流增益。
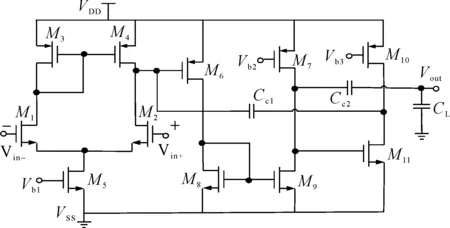
图1 NMC三级运放电路
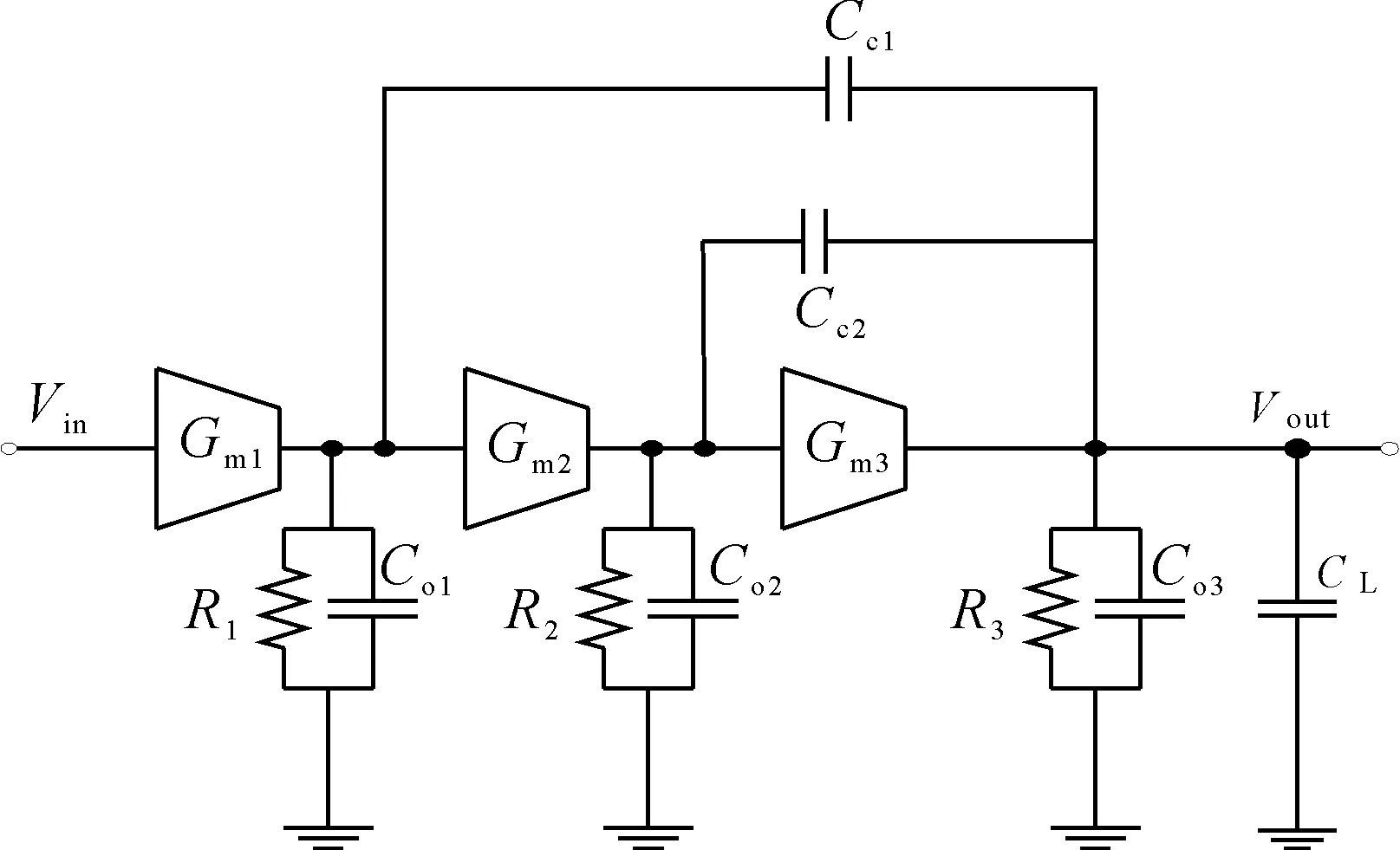
图2 NMC三级运放小信号等效电路
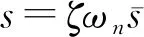
(2)
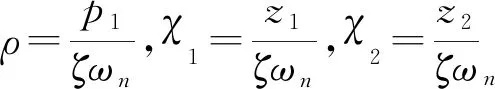
(3)
运放的建立时间ts定义为:
(4)
即单位阶跃响应落入[1-ε,1+ε]区域所需的时间t,ε是建立精度要求。对给定的建立时间精度,文献[5]通过如下的数值优化:
(5)
求出建立时间最小时的参数ρ,ζ。在给定各级跨导Gmi下,式(2)中的参数χ1,χ2由ρ,ζ决定,因此式(5)的优化只需对ρ,ζ进行。由此得到ρ,ζ后,可得建立时间最小时的补偿电容[5]:
(6)
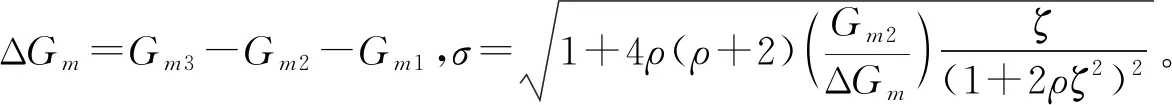
按上述方法进行运放的设计,先根据噪声、摆率、功耗等性能指标要求确定各级的跨导、偏置电流,再由gm/Id参数确定各MOS管的尺寸,最后由式(6)求得使建立时间最小的2个补偿电容。但由于图2及对应的闭环传递函数(1)和(2)是在忽略了运放小信号等效电路中各种寄生元件后的近似表示,因此获得的设计结果是不准确的。对上述放大器,分别指定1.00%、0.10%建立精度要求,按式(5)和式(6)进行计算,得到的电路闭环阶跃响应如图3所示。其中3rdorder model表示用MATLAB计算的三阶闭环传递函数阶跃响应,simulation是对电路进行HSpice瞬态仿真获得的波形。可以看出,2种波形总体上基本一致。但放大后观察从上升到稳态附近的建立过程,可以发现,基于传递函数模型设计得到的拉氏反变换结果满足建立精度要求,波形上升到接近稳态后全部位于要求的精度范围内;而对应仿真波形的上升过程却超过了要求的精度范围,建立时间增大了不少,不能达到建立时间的最小化;且建立精度ε越高,产生的差距越大。因此,得到设计结果后还需经人工调试才能达到真正的建立时间最小化。

图3 NMC运放基于三阶传递函数模型设计的阶跃响应波形
2 建立时间最小化的准确设计
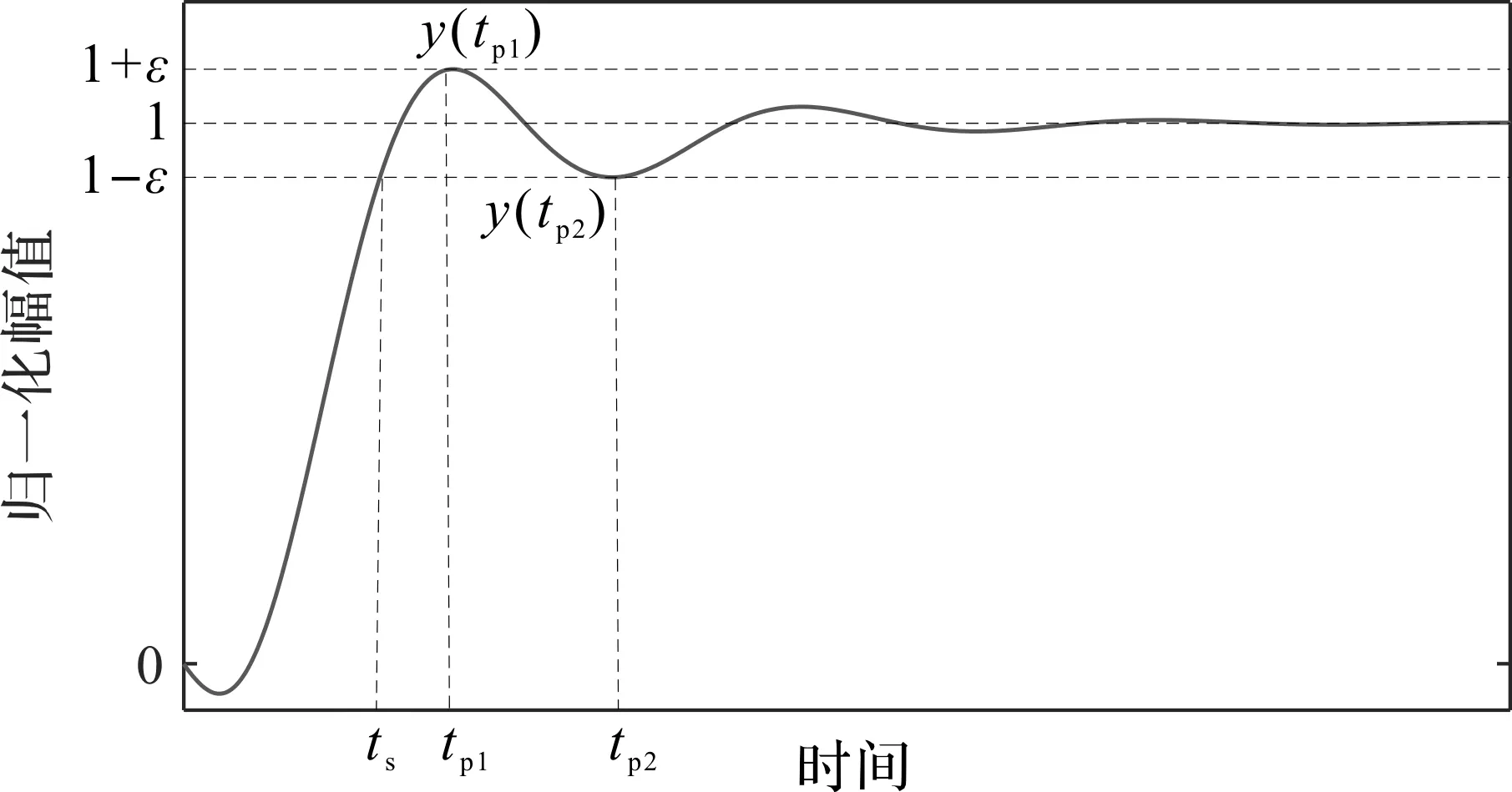
图4 三阶系统时域阶跃响应
对于三阶运放,文献[5]经计算得到的建立时间最小化条件是:其阶跃响应的第1个波峰y(tp1)紧贴指定建立精度对应误差带上限,紧接着的波谷y(tp2)紧贴误差带下限,即如图4所示的情形。换言之,对于给定的建立时间精度ε,三级运放建立时间最小时应满足如下方程:
y(tp1)=1+εy(tp2)=1-ε
(7)
在电路中各MOS管确定的情况下,运放的实际闭环阶跃响应取决于2个补偿电容,因此可根据式(7)列出建立时间的最小化方程:
yp1(ρ,ζ)=1+εyp2(ρ,ζ)=1-ε
(8)
根据式(6),ρ和ζ与2个补偿电容之间实际是可相互转换的,因此将式(7)直接写成以ρ,ζ为变量的形式。若关于这2个峰值的计算是准确的,则从中解出ρ和ζ,再由式(6)算出2个补偿电容,最后获得使运放建立时间最小化的准确设计结果。
式(8)显然是非线性的,本文采用通常求解非线性方程的Newton-Raphson迭代法。峰值的计算通过对运放的晶体管级电路仿真实现,以保证精度。迭代求解首先要有一组初始解,众所周知,初始解的具体位置对迭代的收敛性影响很大。由于三阶传递函数是实际运放特性的一个近似表征,故采用三阶传递函数建立时间最小化设计得到的结果作为初始值。显然,对三阶传递函数,其建立时间的最小化也满足式(8),只是其中的计算可用式(3)导出的解析公式[5],因此更为快捷。解出初始值后,进行如下Newton迭代:
(9)
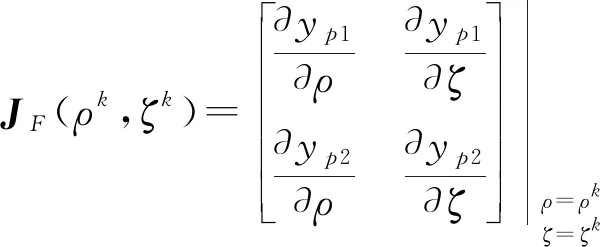
由于三阶传递函数总体上是三级运放小信号特性的较好近似表征,因此从这样的初始值出发,迭代不难收敛。具体速度主要取决于建立精度要求。
3 NMC三级运放设计实例
按照第2节叙述的方法,对图1的NMC三级运放分别在TSMC 0.35 μm和90 nm工艺下进行设计。为便于比较,3个主放大管的gm/Id参数、负载电容(CL)和电源电压(VDD)的大小与文献[5]和文献[9]中的值相同,如表1所示。设计电路的各器件尺寸如表2所示。仿真的输入阶跃信号幅度为10 mV。

表1 三级运放的设计参数

表2 器件尺寸 单位:μm
首先对0.35 μm工艺、建立时间精度ε分别为1.00%,0.10%时的电路进行设计,得到的阶跃响应波形如图5所示。为了便于比较,图中同时给出了此时的三阶传递函数响应波形。从图5可以看出,响应的HSpice仿真波形能准确满足建立时间最小化条件。表3给出了电路的建立时间、带宽、相位等性能指标及2个补偿电容的值,及文献[5]中同样工艺特征尺寸下建立精度为1.00%时的设计结果。可见两者参数差异不是很大,但如图3所示,基于三阶传递函数的结果其实是不满足建立时间最小化条件的。

图5 0.35 μm工艺下,NMC三级CMOS运放建立时间最小化精确设计结果

表3 0.35 μm工艺下NMC三级运放设计结果比较
进一步在TSMC 90nm工艺下进行设计,建立时间精度ε分别为0.10%和0.02%。结果如图6和表4所示。和文献[9]设计结果相比,在相近的相位裕度和较小的带宽下,得到的建立时间更短。
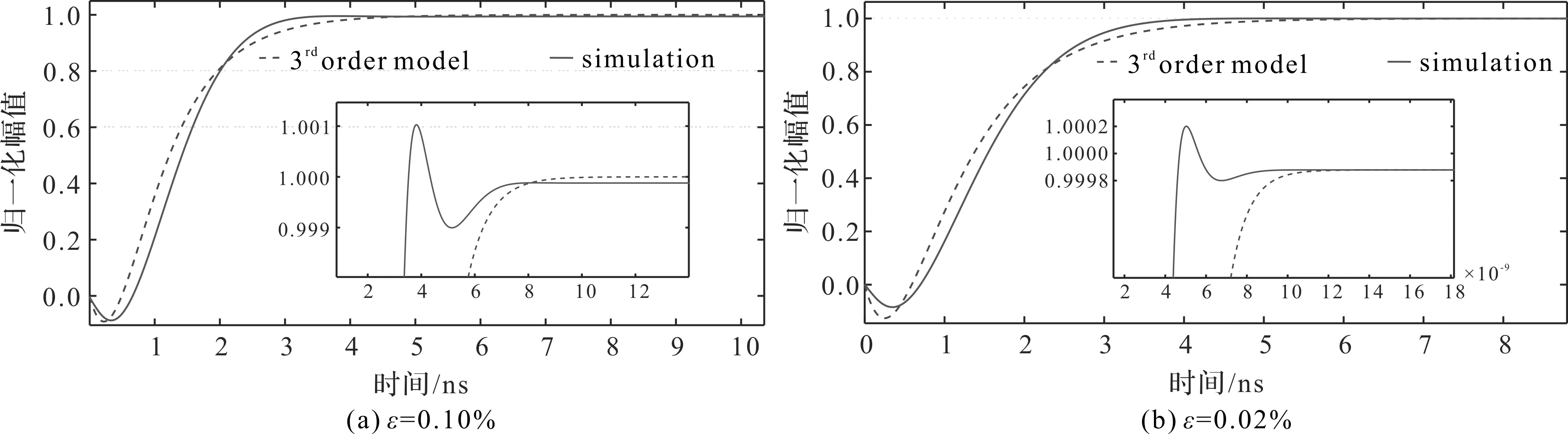
图6 90 nm工艺下,NMC三级CMOS运放建立时间最小化精确设计结果

表4 90 nm工艺下NMC三级运放设计结果比较
上述设计都是在标称或典型工艺下进行的。当工艺参数发生波动时,标称工艺下满足的建立时间最小化条件将不再成立,导致建立时间的增大。为此,本文进行了工艺参数波动时的蒙特卡洛仿真。样本数N=1 000时,分别采用标称工艺下原三阶传递函数模型方法和本文设计方法进行蒙特卡洛仿真的结果如图7所示。可以看出,在工艺参数波动条件下,与原近似设计方法相比,本文方法设计的平均、最小和最大建立时间都更小。
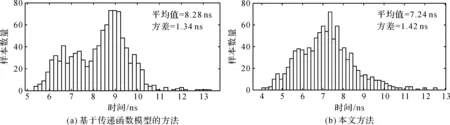
图7 不同设计方法建立时间的蒙特卡洛分析比较
4 结束语
本文提出一种三级NMC运放建立时间最小化的电路级准确设计方法,消除了以往基于近似传递函数模型方法存在的误差,避免了手动调试过程,提高了设计效率。这种迭代设计方法也可推广用于其余不同结构三级运放的设计。在后续版图设计中,因版图的寄生参数还会产生误差,能否采取类似的迭代方法继续消除这种误差,值得进一步研究。

