区间二型T-S模型网络系统的安全控制设计
陈洪军,周绍生
(杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
随着通信网络开放性的提高,网络控制系统(Network Control System,NCS)越来越容易受到恶意攻击者的各种攻击。网络攻击是NCS遭受攻击的主要威胁,主要包括拒绝服务(Denial of Service,DoS)攻击[1]、欺骗攻击[2]和重放攻击[3],其中DoS攻击为NCS安全问题中一种常见的最易实现的攻击形式[4]。恶意攻击者通过占用控制系统中通信网络资源,致使系统的控制信号和测量信号无法正常传输,造成大量数据丢包,给NCS带来危害。因此,研究者们采用安全控制策略来缓解DoS攻击对NCS的影响。例如,文献[5]研究了DoS攻击下切换系统的事件触发滑模控制,运用攻击概率和补偿后的输出信号,设计了动态输出反馈滑模控制器;文献[6]针对一类多智能体系统,设计了适用于DoS攻击的事件触发机制,得到了保证系统模型安全的一个新的充分条件。文献[7]针对一类事件触发网络控制系统,提出了一种基于安全性能的弹性触发方法,但未考虑系统的不确定性。文献[8]通过马尔可夫过程来描述DoS攻击行为,用马尔可夫跳的转移频率来表示DoS攻击发生频率。目前,针对区间二型T-S模型网络控制系统网络攻击问题的相关研究比较少。同时,在实际应用的工程系统中,被控对象含参数不确定也是造成系统不稳定的重要因素。为此,本文在文献[7]的基础上,考虑了系统参数不确定的存在,并使用区间二型T-S模糊模型对网络系统进行建模,设计了含有DoS攻击及模糊系统参数不确定的安全控制器。
1 系统描述
区间二型T-S模型用IF-THEN规则描述为:
Rulei: IFg1(x) isH1i, andg2(x) isH2i, …, andgp(x) isHpi
Z(t)=Cix(t)+Fiu(t)
(1)

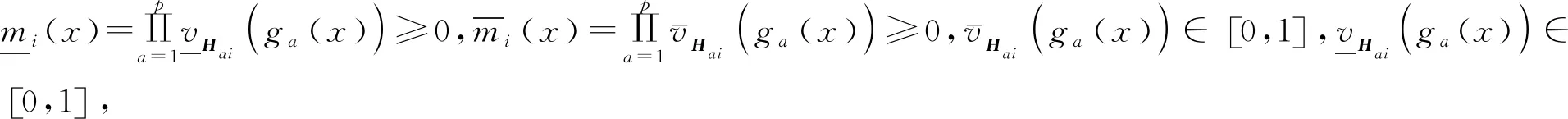
区间二型T-S模糊系统全局模型描述为:
(2)
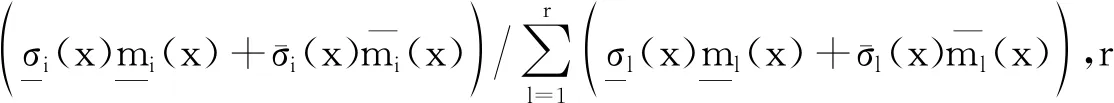
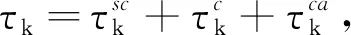
(3)
e(ikh)=x(ikh)-x(tkh)
(4)
式中,e(ikh)表示当前时间的过程状态x(ikh)值与最新一次成功控制更新的过程状态x(tkh)值之间的误差。为记录预先设计的触发时刻tk+1h和x(tk+1h),事件触发器需要一个缓冲区。由DoS攻击引起的额外误差为eDoS(ikh):
eDoS(ikh)=x(ikh)-x(tk+1h)
(5)

(6)
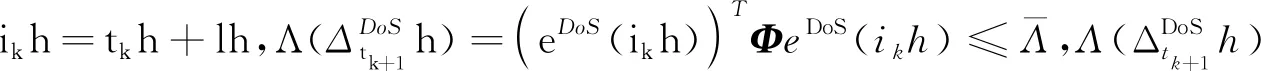
采用并行分布补偿原理设计模糊状态反馈控制器,模糊控制规则描述为:
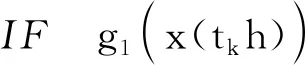
THENu(t)=Kjx(tkh),t∈[tkh+τk,tk+1h+τk+1),k=1,2,…
(7)
通过定义d(t)=t-ikh,t∈Ωl表示每2个成功传输的时刻所造成的延时,dm≤d(t)≤dM。
状态反馈控制器的全局模型为:
(8)
(9)
引理1[10]对于任意适当维数实数矩阵Γi,Ηi(1≤i≤r),S>0,有
(10)
引理2[11]给定适当维数矩阵Π,E和对称矩阵Χ,那么Χ+ΠΚ(t)E+ETΚT(t)ΠT<0,对所有满足KT(t)K(t)≤I的矩阵K(t)成立。当只有满足常数ε>0时,使得:
Χ+εΠΠT+ε-1ETE<0
(11)
引理3[12]标量b>a>0,适当维数正定矩阵Z,使如下积分不等式成立:
(12)
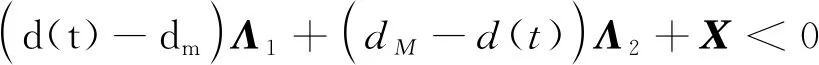
2 主要结果

(13)
(14)
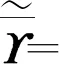
则在弹性事件触发(6)下,区间二型闭环系统(9)通过控制增益Kj=XjY-1作用可以得到:
(1)当没有DoS攻击时,区间二型闭环系统(9)渐进稳定并且满足Η∞性能;
证明构造如下Lyapunov-Krasovskii泛函
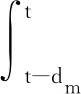
(15)
式中,P,Wl,Ql(l=1,2),是适维正定对称矩阵。为便于描述,定义
沿着系统轨线对V(t)求导,得到:
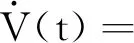
ZT(t)Z(t)-γ2ωT(t)ω(t)-ZT(t)Z(t)+γ2ωT(t)ω(t)+eT(ikh)Φe(ikh)-eT(ikh)Φe(ikh)
(16)
式中,
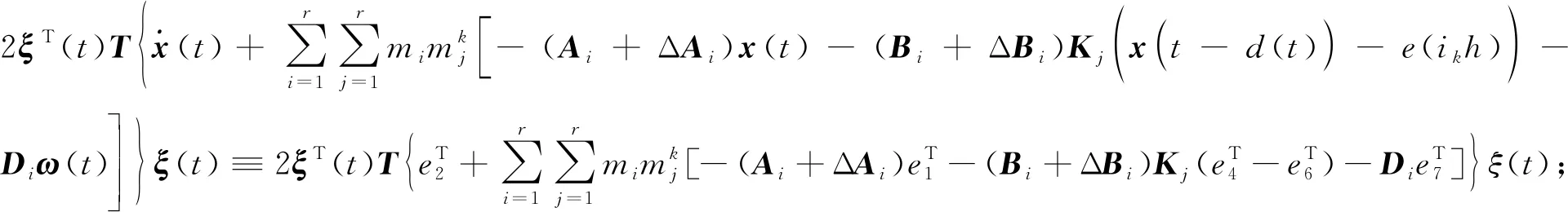
(17)
(18)
(19)
由不等式-2aTb≤aTVa+bTV-1b及引理3,可得:
(20)
(21)
(22)
联立式(15)—式(22)及引理1可得:
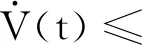
(23)
令
Θ=
(24)
所以式(23)满足:
(25)
采用凸组合方法,结合引理4可得式(24)等价于:
d(t)=dm,
(26)
和
d(t)=dM,
(27)
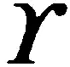
(28)

(29)
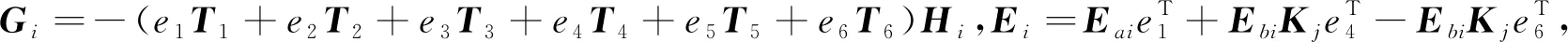
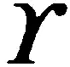
(30)
(31)
对式(31)两边同时在t∈[0,∞)上积分,由零初始条件V(0)=0,V(∞)≥0得到:
(32)
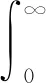
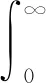
(33)
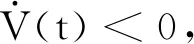
(34)
由于Θ<0,所以必存在一个合适的正数τ,ξT(t)Θξ(t)≤-τV(t),结合式(34)可得:
(35)
式(35)两边同乘eτ t并积分可得:
(36)
所以
(37)
即
(38)
式中,λ(P)为P中的最小特征值。显然系统的性能损失只与式(37)中的最后一项有关,性能损失β满足:
(39)
由式(38)—式(39)可以得到保证系统安全性能的条件。证毕。
3 数值示例
当r=2时,区间二型模糊网络系统的参数选取如下:
对于定理1中给定的参数,选取
ε1=1.1300,ε2=1.328 5,ε3=1.428 7,ε4=0.574 6,ε5=1.0,ε6=0.9,ζ11=10.0,ζ12=10.0,ζ21=5.0,ζ22=10.0,dm=0.001,γ=0.8,σ=0.4
其定义的非线性函数与归一化隶属度函数分别为:
使用MATLAB中的LMI工具箱求得时滞上界dM为0.731 6,并求得可行解为:
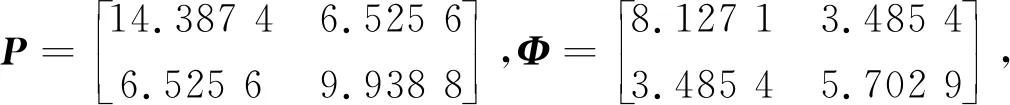
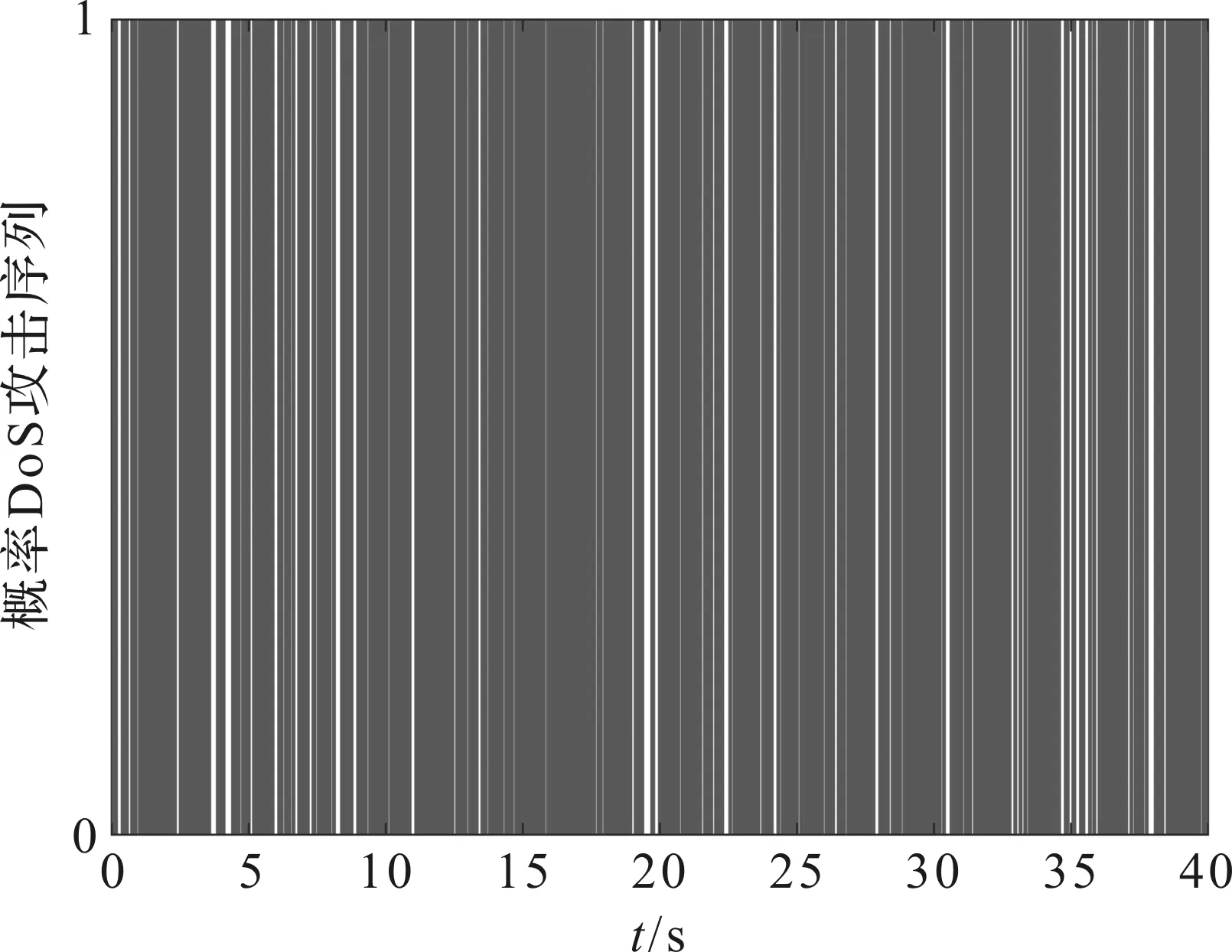
图1 概率DoS攻击序列
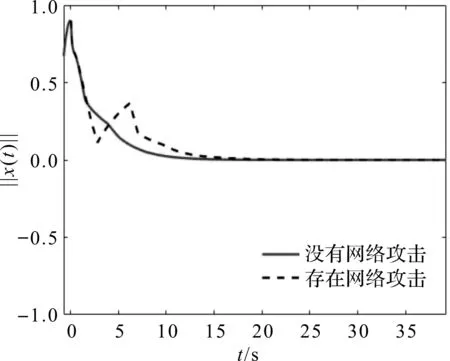
图2 系统状态范数响应

图3 ξ(ikh)恒为1时系统状态范数响应
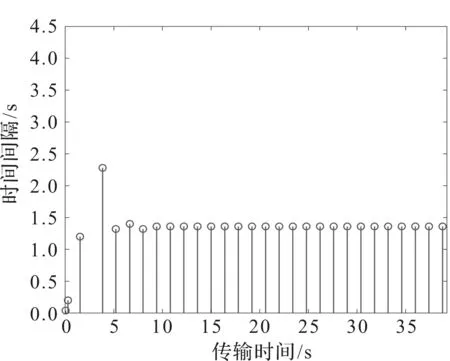
图4 无攻击时事件触发时刻与时间间隔
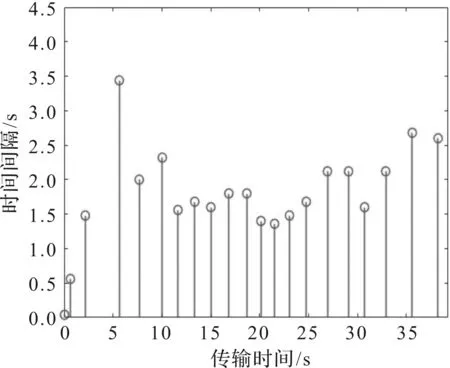
图5 概率攻击时事件触发时刻与时间间隔
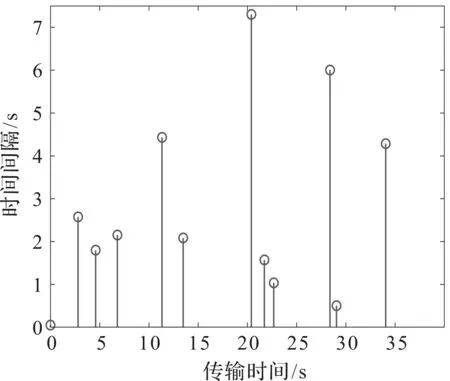
图6 ξ(ikh)恒为1时事件触发时刻与时间间隔
4 结束语
本文研究一类具有系统参数不确定的区间二型T-S模型网络系统在DoS攻击下的安全控制问题,分析了系统在无攻击时的Η∞性能和有攻击时保证安全性能的条件,并设计了弹性事件触发下的安全控制器。下一步将针对其他攻击类型展开进一步研究。

