一种基于扩频信号的散射通信信噪比估计方法

沈斌松， 秦建存

(1.中国电子科技集团公司 第五十四研究所，河北，石家庄 050081；2.中电网络通信集团有限公司，河北，石家庄 050081)

对流层散射通信是一种利用对流层大气不均匀性对微波的散射作用来实现的超视距通信方式，具有传播媒质稳定可靠，抗窃听、抗截获和抗干扰能力强等优点，可跨越海岛、沙漠、湖泊、沼泽等天然屏障和特殊地域，在各国军用无线通信系统中得到广泛应用.

随着战争模式数字化、网络化、信息化发展演进，军用通信系统在通信带宽、可靠度、适应性和业务承载能力等诸多方面的需求不断提高.传统对流层散射通信设备传播可靠度表征在每年慢衰落最坏条件下可靠通信的能力，对其余大部分时间内明显好于最坏月份的信道传播特性未加以充分利用，采用速率自适应技术可实现散射通信系统的通信容量和质量大幅度提升.因此，以速率自适应技术为代表的新体制散射通信系统应运而生.

信噪比(signal to noise ratio，SNR)是一个表征散射信道特性的重要参数，Turbo或LDPC迭代译码、自适应编码调制、自动功率控制、自适应跳频和自动天线对准等功能均需准确的信噪比信息，因此，找到适用于散射通信的信噪比估计算法对提升散射通信系统能力具有重大意义[1].目前，对高斯白噪声(AWGN)信道下的信噪比估计方法已日趋成熟，常见的估计算法有最大似然(ML)估计算法、信噪平方比噪声方差(SNV)估计法、二阶四阶矩(M2M4)估计法以及信号方差比(SVR)估计法等[2-3].但散射信道为典型的多径衰落信道，频率选择性衰落严重，传统信噪比估计方法根据接收到的探测信号进行信道响应估计并计算信噪比，而非信道的实际信噪比[4]，或者依赖解调后信号进行信噪比估计[5].

本文基于散射通信系统的特点，介绍散射通信信噪比估计模型，使用一种基于扩频信号的信噪比估计方法，并提出一种适用于散射通信的等效信噪比算法，获取通信系统的实际信噪比，通过仿真验证本文提出的信噪比估计方法能够有效估计散射通信信道的信噪比，并且等效信噪比的计算结果与实际通信效果一致，简单实用.

1 散射通信信噪比估计

散射通信信道是一种典型多径衰落信道，根据信号带宽与多径时延展宽的关系，信道表现为平坦衰落和频率选择性衰落，并且散射信道具有显著的快衰落特征，严重影响通信质量，需采用分集接收技术平滑信号衰落.因此，散射通信信噪比估计模型应适用于以上两种情况，估计模型如图1所示.

假设有M个分集通道，各个分集通道的衰落过程hm(t),(m=1,2,…,M)是相互独立的离散L径结构，各个分集通道存在相互独立的零均值加性高

图1 散射通信信噪比估计模型Fig.1 SNR estimate model in troposcatter communication

斯白噪声nm(t),(m=1,2,…,M)干扰，且具有相同的功率谱密度N0.信道响应hm(t)可表示为

(1)

式中:am,k(m=1,2,…,M;k=1,2,…,L)为第m分集通道多径k的衰落因子，服从瑞利分布;φm,k(m=1,2,…,M;k=1,2,…,L)为第m分集通道多径k的相移因子，服从均匀分布，其时延参数为τm,k(m=1,2,…,M;k=1,2,…,L).

发射信号s(t)经过散射信道后，各分集通道的接收信号rm(t),(m=1,2,…,M)可以表示为

(2)

各分集通道接收信号rm(t)经接收机处理后进行信噪比估计与M通道合并，合并方式不同，合并后信号质量不同，信噪比也存在差异[6].

由于散射通信功率严重受限，要求信噪比估计准确、高效，更要反映信道的多径因素，表征有效信噪比，这对散射通信信噪比估计方法提出新要求.

2 基于扩频信号的信噪比估计方法

2.1 信噪比估计方案

常用的信噪比估计算法分为两类，一类基于数据辅助(DA：data-aided)，即在信道中周期性的发送导频或训练序列；另一类非数据辅助(NDA：non data-aided)，即直接对接收信号进行处理.本文采用基于扩频信号辅助的信噪比估计方法，其数据帧结构如图2所示，每个数据帧时长4 170 μs，RU为功率上升时间，RD为功率下降时间，HEAD为帧头信号，用于数据帧定位，DET/CTRL为探测/控制信号，用于信噪比估计并同时控制调制与编码方式，DATA为业务信息.

表1 信噪比估计方法数据帧结构Tab.1 SNR estimate method data frame structure

为准确估计信道多径，探测信号应覆盖整个工作带宽，为进一步提高传输效率，采取探测与控制信号同传方案.为满足以上要求，探测/控制信号采用线性调频信号，具有恒包络特性，其表达式为

(3)

式中:μ=2πB/T为信号变频速率因子;B为信号带宽;T为信号周期;φ为相位信息，用于传输控制信息.线性调频信号是一种具有良好自相关特性的信号，匹配后信号由恒包络信号变成窄脉冲信号，即将原来在码元时间T内均匀分布的信号能量大部分集中于峰值点附近，匹配后信号可以表示为

(4)

匹配后信号的包络呈辛格函数的形状，其脉冲宽度τp=1/B，主峰两个零点间宽度为2/B.因此，匹配滤波器可实现分离多径，多径分辨率为1/B[7].线性调频信号的匹配与多径分离如图2所示，LFM信号带宽为50 kHz，主峰两个零点间宽度为0.04 ms，当多径时延为0.02 ms时即可实现多径分离.

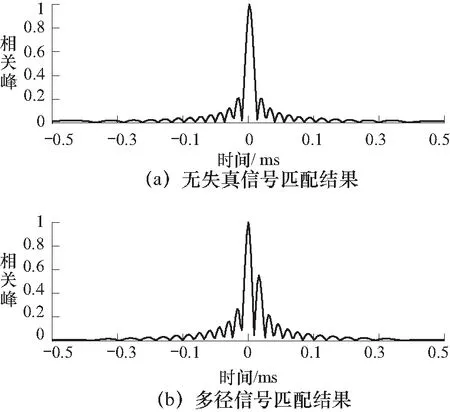
图2 线性调频信号的匹配与多径分离Fig.2 LFM signal match receive and multipath separate

2.2 基于扩频信号的信噪比估计方法

若接收信号匹配后的相关峰能量大于最大相关峰能量的5%，即判定其为多径信号.假设依照上述准则线性调频信号可分离L条多径，则无分集时接收信号表示为

(5)

则接收信号解扩后可获得各个多径分量的相关峰ak，得到接收信号的信噪比，可以表示为

(6)

式中K为信噪比常数，只与基准通信速率有关.式(6)得到的信噪比估计值与其他基于探测信号的信噪比估计方法一致，由于线性调频信号在解扩过程将各个多径分量的能量集中到相关峰，因此可提高多径信道估计的抗噪声性能[8].

使用表1所示的数据帧结构，信道设置为多径功率分布如表2所示的5径信道，分别对本文提出的算法与M2M4算法的信噪比估计性能做仿真对比，仿真结果如图3所示.

表2 信道多径能量分布

由图3可以看出，M2M4算法在多径信道下失效，利用均衡后信号得到的信噪比估计值在信噪比较小和较大时估计误差较大；采用本文提出的信噪比估计方法在信噪比0～30 dB时得到的估计值接近真实信噪比，估计误差小于0.5 dB，估计准确，性能优于M2M4算法.

图3 信噪比估计算法性能对比曲线Fig.3 Performance of SNR estimate method

当系统有M个分集通道时，假设线性调频信号仍可分离L条多径，接收信号用式(2)表示，则各个通道的信噪比可表示为

(7)

合并方式不同，得到的合路信噪比也不同，常用合并方式下的合路信噪比如表3所示.

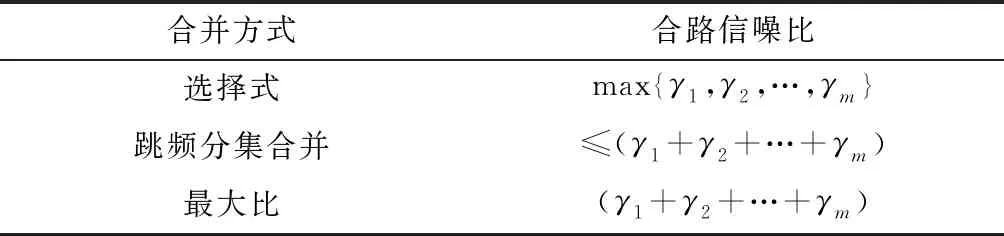
表3 常用分集合并方式下的合路信噪比

3 等效信噪比估计算法

3.1 失真自适应接收

当信道多径小于设计的保护时间时，采用失真自适应接收机(distort adaptive receiver，DAR)消除并利用信道多径，基于扩频信号的DAR工作原理如图4所示(假设可分离出2个多径).DAR接收机将接收信号在时域压缩成多径分离的窄脉冲信号，采用逆调制方式提取与窄脉冲信号同频、同相、同包络的载波信号，并与窄脉冲信号进行积分合并处理，实现匹配接收，即最佳接收功能[9].

图4 基于扩频信号的DAR工作原理图Fig.4 DAR principle base on spread spectrum signal

根据图4所示的DAR工作原理可知，该接收机可收集并利用多径信号并进行最大比合并，其接收信号的等效信噪比与第2节获得的信噪比或合路信噪比一致.

3.2 自适应均衡接收

当信道多径超出设计的保护时间时，采用自适应均衡技术消除信道多径.均衡器的工作原理不再赘述，当均衡器的输入为式(2)所示的接收信号时，均衡器在各个分集通道找到其最大径信号，并以此为基础消除其余多径信号[10-11].因此，均衡器仅利用最大径信号，其单路最优解可表示为

y(t)=us(t)+n(t)，u=max{a1,a2,…,aL}

(8)

因此，接收信号的单路等效信噪比表示为

γ=Ku2/N0

(9)

比较式(6)和式(9)可知，均衡器输出信号的等效信噪比小于其估计信噪比，并且多径分量越多相差越大.

当系统有M个分集通道时，各个通道的等效信噪比表示为

(10)

其等效合路信噪比仍可按照表3中的公式计算.

使用表1所示的数据帧结构，采用BPSK调制，工作带宽30 MHz，传输速率分别为150 kbits/s和6 Mbits/s，信道设置为多径能量分布如表4所示的二重分集信道，接收信号处理分别采用DAR和均衡解调与最大比合并，对其误码性能做仿真测试，测试结果如图5所示，同时将等效信噪比估计结果对应的误码率绘制于图5中.

表4 信道多径能量分布

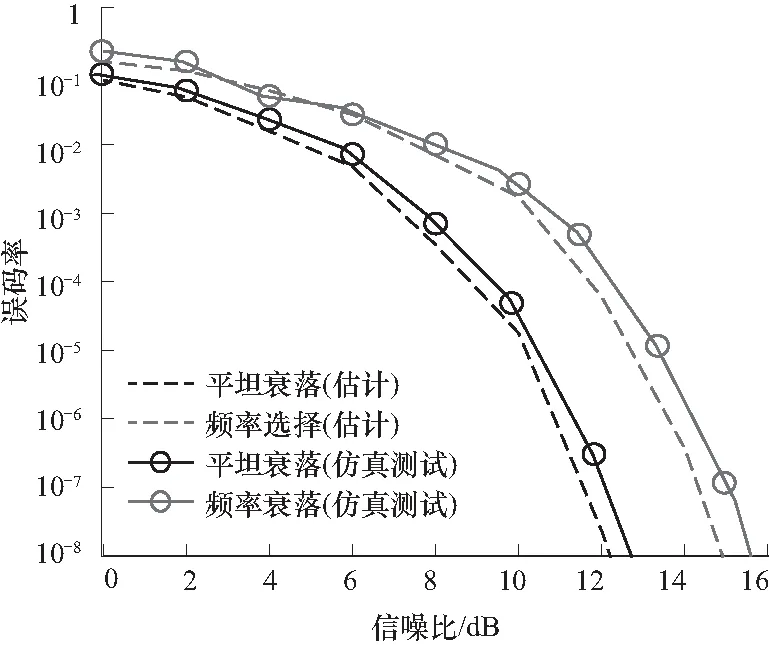
图5 误码率仿真测试结果Fig.5 Simulation result of bit error ratio

由图5可知：

① 平坦衰落信道下，误码率仿真测试曲线与估计所得等效信噪比误码率曲线相吻合，估计误差小于0.5 dB；

② 频率选择性衰落信道下，误码率仿真测试曲线与估计所得等效信噪比误码率曲线相吻合，估计误差小于1 dB，性能损失大于平坦衰落信道，这与均衡器导致的噪声非白化有关；

③ 平坦衰落的仿真测试误码性能优于频率选择性衰落约3.5 dB，即平坦衰落的等效信噪比优于频率选择性衰落，与理论分析结论一致.

综上所述，等效信噪比估计值与实测曲线吻合，该信噪比估计算法以及等效信噪比计算方法正确有效，均可用于散射通信信噪比估计，指导工程实践.

4 结束语

在以速率自适应技术为代表的新体制散射通信系统中，适用于多径严重的散射信道信噪比估计算法至关重要.本文提出一种基于线性调频的信道等效信噪比估计方法，通过仿真表明该算法可在0～30 dB信噪比范围内准确估计接收信号的信噪比，并且进一步给出常用分集接收方式下的合路信噪比表达式；在信噪比估计准确的条件下，提出适用于不同接收算法的等效信噪比计算方法，仿真结果表明该方法能够更加准确的表征实际通信效果，对工程实践具有重要的指导意义.