根植习题“土壤” “生长”数学素养

徐剑

[摘  要] 利用课本所赋予的教学功能，关注课本习题的“深加工”，基于“用教材教”的教学理念进行教学，可以促使学生认知结构的不断完善，促成学生思维的不断深化，对于提升学生的数学素养来说更是极有意义. 具体来说，课本习题是引出新知的重要源泉，习题多解是拓展思维的内在活力，习题变式是深化理解的外在助力，习题拓展是获得一般结论的不竭动力.

[关键词] 课本习题;一题多解;变式;拓展;数学素养

从课程改革实施至今，从关注学生“双基”的培养到当下的核心素养的培育，越发凸显教学的创造性和发展性. 这样的大环境下，不少教师尽管已经意识到课堂重心需要转变，却没有认真思考如何实现这样的转变，在教法和学法上保留着原有方式，停留在“教教材”的教学模式，无法在真正意义上提升学生的素养.

课本习题是编者从知识内容和课程标准的要求出发精心设计而成的，具有一定的典型性和发展性，是丰富教学设计的良好素材，是数学思维的生长点. 教师的教育智慧体现在对教材的准确理解和教学理念的精准贯彻，从而教师需要吃透课本精神与实质，细细揣摩每个习题，利用课本所赋予的教学功能，关注到课本习题的“深加工”，基于“用教材教”的教学理念，充分实现教学理念与课堂教学的完美契合，为学生开辟一条数学学习的新天地.

课本习题是引出新知的重要源泉

不少教师只知课本习题在巩固基础知识技能方面的效能，却忽视了课本习题在新课引入时同样具有重要的意义. 良好的开端是成功的一半，富有创意地进入新课是每个教师需要深思的问题，也是长久以来困扰教师的一个难题. 课本习题是引出新知的重要源泉，倘若从学生的已有认知结构出发，基于学生的最近发展区，以课本习题为新知的生长点创设情境，通过问题引领，同样可以让学生产生主动探究的欲望，促进思维活动的有效推进.

案例1：以“双曲线”的导入为例.

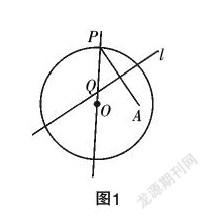
出示习题：如图1，已知圆O内有一定点A，且定长r为圆O的半径，点P为圆O上的一个动点，线段AP的垂直平分线l与半径OP交于点Q，试说出随着点P在圆O上不断运动时点Q的轨迹，并说明理由.

师：大家还能回忆起这一问题的解答过程吗？结论是什么？（学生经过回忆，七嘴八舌地说出解答过程，并阐明结论“点Q的轨迹是以点O和点A为焦点的椭圆”）

师：刚才大家的回答都非常精彩. 那么，倘若稍加变换问题，将题目的条件“圆O内有一定点A”变为“圆O外有一定点A”，“半径OP”变为“直线OP”，则点Q的轨迹又是什么呢？（学生在自身的已有认知中进行猜想和讨论，课堂气氛火热）

师：下面，通过几何画板的演示来验证大家的猜想. （通过演示，在师生互动和直观中让学生感知一个新的曲线）

师：经过刚才一系列条件的变化，点Q满足什么几何条件？我们该如何刻画诸如此类的曲线呢？（引出课题）

评析：传统数学教学中，教师一般会生硬地抛出概念，让学生自我消化;而本例中，教师从实际出发，以课本习题为载体创设情境，提出与概念相关的典型问题，不仅可以活跃课堂气氛，还可以自然而然地让学生建立感性认知，水到渠成地实现课堂生成.

习题多解是拓展思维的内在活力

日常教学中，开展习题多解的探究可以很好地引导学生全方位地认识和掌握习题，活化所学知识，增强知识之间的联系，同时也可以拓展学生思维的宽度和维度，培养学生灵活多变的思考方式. 因此，教师可以根据具体的教学内容，灵活地选择适合“一题多解”的典型习题，让学生在“一题多解”中积累解题经验，渗透数学思想，拓展思维活力;同时寻求独特而简捷的解题方法，以达到提高解题能力的目的. 这里值得注意的是，习题的多解需要从问题的不同角度展开，标新立异构建不同的思路，而对于一些怪、偏、繁的解法大部分情况下都可以选择略过.

案例2：一海岛长期驻扎着一支军队，海岛离岸边最近的点B的距离为150 km，军需品仓库则设于岸边与点B的距离为300 km的点A处，且点A和点B之间有一条铁路. 仓库内有一批紧急物资需要在最短时间内运送到海岛，可选用海陆联运的方式进行运送. 火车速度为50 km/h，轮船速度为30 km/h，现试着在岸边选择一点C，先火车运送到点C，再从点C处以轮船运送至海岛，那么点C选在何处才能使得整个运输的时间最短？

评析：“一题多解”的目的不仅仅在于解题本身，更在于学生思维的锻炼. 实践表明，学生的解法越多，思路越开阔，思维就越灵活. 本例是一道典型的“一题多解”的习题，可以通过判别式法、换元法、数形结合法、导数法等四种方法进行解答. 通过教师的鼓励、点拨，让“冰冷的美丽”绽放“火热的思考”，激发学生主动探索的热情;学生独辟蹊径，形成了登台展示的火热场面，解法也就源源不断地流淌了出来. 合理而有效地运用好“一题多解”的训练能促进学生思维的生长，在这里得到了很好的诠释.

习题变式是深化理解的外在助力

由于课本中习题是以静态的形式呈现的，且受到篇幅性和精华性的影响，不可能过于完善，从而易淡化学生的探究积极性，无法指引学生进行深入探究. 而课本习题大部分都具有可探究性和可变性. 鉴于此，教师在教学的过程中，若是将教材中静态的数学习题通过联想和变通，以习题变式的形式呈现，则可以活跃学生的思维，帮助学生理解概念的生成过程和法则的发展过程，加深对知识的理解.

案例3：已知函数f（x）为偶函数，且在区间（0，+∞）上为减函数，试判断f（x）在区间（-∞，0）上是什么函数，并予以证明.

变式：已知函数f（x）为奇函数，且在区间（0，+∞）上为减函数，试判断f（x）在区间（-∞，0）上是什么函数，并予以证明.

评析：这是一道典型的习题变式，教师通过对教材习题的充分挖掘与利用，以变式的形式呈现，使得習题教学不再是“就题论题”的模式. 这样利于加深学生对两个常用结论的理解和认识，利于指引学生的思维走向深处;这样学生在教师变式的驱动下探清问题，揭示本质，实现学力的生长. 在这个过程中，学生从中收获的不再是一道数学习题，而是对一类数学问题的理解和一种主动探究的精神.

习题拓展是获得一般结论的不竭动力

一些教师在日常练习中不太喜欢运用课本习题，而会选择从教辅资料中引例或是运用高考题，这是源于他们认为教材习题过于简单，对发展学生的数学思维毫无益处. 对于这一观点笔者不敢苟同. 事实上，教材习题不仅利于夯实“双基”，还可以通过深入挖掘和有效拓展获得一般结论，同时深化学生的数学思维，以达到对数学知识的真正理解.

案例4：以对“三角函数辅助角公式”的探究为例.

出示习题：化简：①cosx-·sinx;②sinx+cosx;③（sinx-cosx）;④cosx-sinx.

评析：以上习题是“两角和与差的正弦、余弦、正切公式”教学中的习题，目的是为了引导学生创造性地逆用公式进行化简. 经过观察可以发现，以上四个习题均具备辅助角公式的一般形式，为了让学生更自然地获得一般性结论，教师可以让学生化简各式，并推导得出辅助角公式;更进一步地，运用辅助角公式再化简以上各式，以此完美地诠释其内涵与外显. 这样的设计中，通过抽象和提炼，循序渐进地使得学生的认知结构从“认识”上升到“理清”的层面，唤醒学生的灵感，拓展得出一般结论，同时使得学生的数学思维又一次向纵深发展.

总之，是否能超越课本习题的固有设计，灵活运用课本习题，除去需正确理解习题的设计意图之外，还需做到对学科知识的整体把握. 相较于其他学科，数学有可能更需要把握教材. 如果能在教学设计中把握数学知识的脉络，关注到课本习题的“深加工”，展开习题多解、习题变式和习题拓展，就能使得教学有的放矢. 只有这样，才能让学生所学知识更系统、更具有迁移能力，才能促进学生数学素养的生成以及数学思维能力的形成.

3251500316570