HPM促进数学教师专业发展：从理论到实践

彭刚 胡晓娟

[摘  要] 教师专业发展是学校发展和影响教育改革成败的重要因素. 如何有效地促进教师专业发展，既是教师教育研究中的重要课题，也是教学实践中影响学校教育质量的关键.文章从教师知识以及教学信念两个方面，论述了数学史与数学教学的有机融合对于数学教师专业发展的积极意义，并提出了实现这些教育意义的途径与方式.

[关键词] 数学史;数学教学;教师专业发展

“教育大计、教师为本”，教师是教育构成要素中的关键因素，教育是否能够得到有效发展、教育改革是否能够取得成效，教师的作用举足轻重. 鉴于此，许多国家和地区的教育部门都很关注教师专业发展，并把这项工作视为改善教育的重要途径.

众所周知，我国传统的数学教师培养方式和提升机制有着自身的独特性，在提升数学教师的教学技能、丰富他们的教学经验等方面有一定的优势[1]. 然而，近十年来我国数学教育的理念不断在更新，课程标准也不断在变革，一线教师不仅面临着与教育理论的冲突，同时也遭受了教学实践的挑战.在这种情况下，他们所面临的压力越来越大，普遍存在的职业倦怠问题可能会进一步加剧. 长此以往，教师的教学效果和工作状态都会受到影响，这不利于学生的发展，对整个学校教育的质量也会产生负面效应.

因此，如何有效地促进在职教师的专业发展，不仅是教师教育研究中十分有价值的课题，同时也是当前教育实践中亟待解决的问题. 本文主要探讨的是数学史融入数学教学这一过程，对数学教师的专业发展有哪些教育意义，以及实现这些教育意义的可能方式.

HPM概述

人们对于数学史的教育意义的关注已经有很长的时间. 事实上，早在19世纪一些欧美数学家和数学教育家在这方面发表过很多有益的见解. 然而，从世界范围来看，正式的相关国际组织——数学史与数学教学关系国际研究小组（International Study Group on the Relations between History and Pedagogy of Mathematics，简称HPM）的成立在1972 年.在英国埃克塞特（Exeter）召开的第二届国际数学教育大会上，该小组宣布成立并于1976 年开始隶属于国际数学教育委员会（ICMI），从而引起了人们对于数学史的教育价值的广泛关注.

如今，对于我国大多数数学教育工作者（包括一線教师）而言，HPM 已不再是一个十分陌生的名词. HPM本身是一个组织的名称，但现在它更多的时候是代表一个研究领域，其内涵也常常被理解为“数学史在数学教学中的渗透”或者“数学史融入数学教学”[2].

HPM领域的研究内容十分丰富，目前学者们主要关注以下几个方面：“为何”融入数学史、“如何”融入数学史、教育取向的数学史研究、HPM案例开发、学生理解数学的历史相似性研究、数学史融入教材研究，以及本文主要探讨的HPM与教师专业发展.

HPM对于教师专业发展的意义

教师专业发展是当前教育领域的热点话题，其内涵是教师作为专业人员，不断提升自己对于数学以及数学教学的认识，不断拓展自我专业知识与技能以及不断完善和丰富自我专业理想等发展过程.格伦迪和鲁滨孙认为教师专业发展有三个基本目的与功能[3]：第一个目的是“拓展”，指教师在自我基础上拓展自身的知识和技能;第二个目的是“更新”，指教师利用新的理论和教学实践，更新原有的旧知识和理念;第三个目的是“成长”，指教师在知识广度和深度以及技能的熟练度方面有所提升.

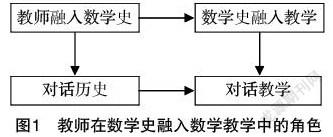
格伦迪和鲁滨孙的观点主要考虑的是教师知识、技能方面的成长.实际上，教师将数学史与数学教学的有机融合过程，既是教师将自己与数学史知识有机融合、将数学史融入教学的过程，同时也是教师理解相关数学史知识、对以往教学设计反思的过程（如图1）.

在这个过程中，教师的专业知识会得以增长，数学信念也会得到转变.因此，HPM对于数学教师专业发展主要有以下两个方面的意义.

1. 教师知识的增长

一般而言，教师的知识主要分为两类：“理论性知识”和“实践性知识”[4]. 其中，数学教师的理论性知识主要包括数学内容知识、数学教学知识、学生如何学习数学的知识，等等. 实践性知识则包括教师在数学教学中实际使用和表现出来的知识，这一类知识往往用教学情境、教学设计或者教学案例呈现.

在数学史融入数学教学的这一过程中，数学教师既可以增加自己的理论性知识，也能够丰富自己的实践性知识.

第一，数学史是一种巨大的资源，可以提供大量的数学问题和问题解决的方法，同时数学史还揭示了数学概念、思想的起源与发展. 因此，教师在理解相关数学史知识、融入数学史的过程中，可以获得新的内容知识（Content Knowledge）.

以数学概念教学为例.众所周知，概念是数学理论的基石，因而概念教学是数学教学的重要组成部分. 然而在实际教学中，许多教师对于这些概念的来源并不十分清楚，往往教学中一带而过，不利于学生形成对于数学的正确认识.事实上，许多数学概念都有其历史来源和人文内涵，教师对这些概念的历史考察，便可以获得关于数学概念的一些新知识. 下面我们以“数系的扩充与复数的概念”这一内容的教学为例做较为详细的说明.

按照通常的引入方式，人们往往把虚数的产生归结为由于方程x2+1=0在实数范围内没有解，事实上这种说法很难揭示出虚数产生的必要性. 如果教师能够去挖掘虚数产生的历史背景，就会发现其背后有着更为合理的解释以及更为重要的历史意义：（1）虚数的产生是由于三次方程的求根公式在一些情况下不能使用;（2）虚数的名称来自英文单词imaginary number，虚数单位i则来自上述名称第一个单词的首字母，意思是“虚无缥缈的数”;（3）一些数学家给出了虚数的几何解释，从而消除了人们对于虚数的疑虑;（4）虚数的产生大大丰富了数学理论，同时还促进了物理学的研究.

由此可以发现，数学的历史发展可以帮助教师揭示出数学概念产生的原因，拓展他们的数学视野，并在此基础上也让学生了解数学知识的价值与意义.

第二，由于学生对于数学知识的一些误解和学习障碍与历史上的错误和认知障碍具有很大的相似性，因此了解历史上的重要时刻便可以为教师提供预测学生认知障碍的工具. 教师在反思以往教学设计基础上，可以形成新的、更有利于学生理解的教学设计，同时获得新的情境知识、案例知识等实践性知识. 以函数概念教学为例，函数概念在初中和高中均有定义，那么这两个定义之间有怎样的关系呢？这需要从历史来考察. 学生在初中学习了函数概念之后，往往会误认为函数就是一个表达式，这与历史上大数学家欧拉的观点一致，因此也是有一定的合理性的. 教师如果了解了函数概念的历史发展，就会根据历史上数学家对于函数的认识，来设计这一内容的教学，引导学生从“变量说”转向“对应说”，从而更好地理解函数概念.

总之，教师知识的增长，将会为数学教学注入新的活力.

2. 教师信念的转变

教师的数学信念主要包括教师对数学本质的认识、教师如何进行教学、学生如何学习数学等三个方面. 其中，教师对于数学本质的信念起着决定性的作用，它会影响到教师对数学“教”与“学”的看法，进而影响到教师怎么教和如何教.

一般而言，如果一名教师倾向于绝对主义数学观，那么他（她）在教学中就很有可能会静态地看待数学知识，并原封不动地传授给学生，这种情况下学生容易形成对于权威的崇拜，认为数学是绝对真理，不利于数学理性精神的培养. 反之，如果一名教师持有可误主义数学观，那么他（她）就会重视探究活动的重要性，从试误中总结出正确的方向，重视知识的发生发展过程，有效地提升学生的数学理解[5].

与传统数学教学中充斥着的大量的数学解题、应试技巧不同，数学史主要研究的是数学概念、数学方法和数学思想的起源与发展，以及其与其他学科（如天文、物理、生物、化学等等）和一般文化的联系.漫长的数学发展历史告诉我们，数学并不是一个僵化的真理系统，而是一门不断演进、人性化的学科.因此，在与数学史对话的过程中，教师不仅可以了解到数学与天文学、建筑学、物理学之间的联系，还可以更好地认识“做数学”的创造性过程.

在将数学史融入数学教学的过程中，持绝对主义数学观的教师便有可能改变对于数学的看法.教师数学信念的转变，既会带来教学理念、教學设计、教学行为的转变，同时学生也会在教师的这种转变中改善自身的数学信念，从而提高自己的数学学习质量.

HPM促进教师专业发展的方式

教师专业发展的实施主要有三种策略[6]：（1）以学校作为教师探究和发展的主要空间，即坚持以校为本（school-based）的理念;（2）构建高等院校与中小学的合作共同体，旨在通过平等、互惠的伙伴协作（partnerships）来改善教师课堂教学;（3）建立网络（networks），把分散的、作为个体的教师集中在一个有机的网络群中，利用网络资源促进教师共同发展.

由于数学史课程在传统师范教育以及教师在职培训中还不够深入，我国中小学教师的数学史素养又不容乐观，然而大学在数学史专业性方面往往有较大的优势，故大学和中小学合作（即上述第二条策略）是实现HPM促进教师专业发展的主要策略.

大学教师和中小学教师合作，可以形成一个教学共同体（teaching community）. 教学共同体的建设，可以促使大、中小学教师之间的优势得到互补，形成教育教学的合力，减缓教师的心理压力，充分发挥教师自身的教育潜能，真正解决教育教学中的具体问题[7]，使得先进的教育理念能够在课堂教学中发挥积极的作用. 在这个共同体中，大学主要提供数学史方面的资源以及专业建议，中小学教师则主要是教学设计者以及教学实践者，具体合作的流程如下：确定课题→选取相关素材→HPM教学设计与实施→评价与反馈→形成HPM案例.

下面我们对上述流程进行简要的说明.

第一，由一线教师根据教学计划以及学生情况，选择自己感兴趣的课题.

第二，由高校教师选择合适的相关数学史素材. 这些素材既可能来源于数学史的原始文献，也可能来源于数学史著作或者数学家的传记等等. 考虑到一线教师以及学生的接受能力，高校教师与一线教师需要对素材进行不断审察与甄选，尽量将数学史的史学形态转化为数学史的教育形态.

第三，由一线教师根据上述数学史素材进行相应的教学设计，并与高校教师共同修改. 一般而言，HPM教学设计要兼顾以下几项原则[8]：趣味性、科学性、有效性、可学性和新颖性. “趣味性”，指的是在数学教学中融入的数学史内容对于学生而言具有很强的吸引力，能够激发学生的学习兴趣;“科学性”指的是数学史料的来源应该真实可靠，参考权威数学史家的著作，并且多种来源互相印证以保证符合历史情境;“有效性”指的是融入数学史的目的是为了更有效地实现教学目标，而不是“为历史而历史”;“可学性”指的是所选择的的数学史料学生容易接受，而不能直接介绍学术形态的数学史，教师需要对它们进行教育加工;“新颖性”指的是HPM教学设计需要有所创新，而不能从网络直接复制或者照本宣科.HPM教学设计实施后，一线教师还可根据学生以及其他任课教师的反馈对教学设计不断进行调整、完善，直至最后形成相应的HPM教学案例.

教学共同体的建立和HPM教学案例的形成，不仅可以激发一线教师积极主动参与到研究中，提高他们的教学水平，同时也会让一线教师对教育研究产生认同感. 以上海为例，华东师范大学HPM团队与上海市沪太路教育发展区合作，充分利用大学的学术资源，与数学教师们合作开发了多个HPM案例并在中学教学类杂志上发表. 合作过程中，从课型的丰富到分支的融合，一线教师可以在不同的数学领域找到线索，让教学设计既具有历史感，也与现实有关联. 合作之后，他们对于如何进行HPM教学以及相应的HPM案例开发，都有了深刻的体会和认识，其中有的教师更是认为这些合作带给自己的是一番自我超越的体验.

总之，HPM促进教师专业发展，不仅是量的增加，更是质的改变. 在此过程中，一线教师也不只是数學教师，更是持续的实践探究者和行动的反思者.只有如此，他们才能真正成为专业发展的主体，进而引发教师个体生命的成长与自我潜能的实现.

参考文献：

[1]  黄荣金，李业平. 中国在职数学教师专业发展的挑战与机遇[J]. 数学教育学报，2008，17（3）.

[2]  郑玮，郑毓信. HPM与数学教学中的再创造[J]. 数学教育学报，2013（3）.

[3]  Grundy，S.& Robinson，J. Teacher Professional Development： Themes and Trends in The Recent Australian Experience [A]. In C.Day & J.Sachs （Eds.）， Inter-national Handbook on the Continuing Professional Develop-ment of Teachers. Maidenhead： Open University Press，2003.

[4]  陈向明. 实践性知识：教师专业发展的知识基础[J]. 北京大学教育评论，2003（1）.

[5]  喻平. 教师的认识信念系统及其对教学的影响[J]. 教师教育研究，2007（4）.

[6]  Day，C.& Sachs，J. Professionalism， Performativity and Empowerment： Discourses in the Politics， Policies and Purposes of Continuing Professional Development[A]. In C. Day & J. Sachs （Eds.）， International Handbook on the Continuing Professional Develop-ment of Teachers. Maidenhead： Open University Press，2004.

[7]  任其平. 论教师专业发展的生态化培养模式[J]. 教育研究，2010（8）.

[8]  汪晓勤. HPM视角下的“角平分线”教学[J]. 教育研究与评论（中学教育教学版），2014（5）.