基于Bezier曲线生成3D打印分层路径

尹海涛，叶春生

(华中科技大学 材料成形与模具技术国家重点实验室，湖北 武汉 430074)

3D打印起源于20世纪80年代，是为满足模型制作以及快速成型的需求而推出，现已经成为计算机辅助设计和快速制造的通用技术平台，3D打印可用于陶瓷、金属和聚合物类材料生产，且可实现高效无模成形[1-5]，因而在医疗、汽车、航空航天和建筑领域得到了广泛的应用。

3D打印技术将三维模型切片成二维平面，对每一层二维平面进行打印，逐层叠加形成三维模型。切片过程使用一系列在特定位置且相互平行的平面与三维模型相交，从而得到模型在这些高度上的切点并形成一条或多条闭合路径，闭合路径的精度影响着二维平面的打印精度，从而影响整个三维模型的精度。刘恒、朱心雄[6]提出了STL模型的分层邻接排序快速切片算法，徐敬华、盛红升[7]提出了基于邻接拓扑的流形网络模型层切多连通域构建方法，张琪、孟正大[8]提出了基于三角片分割的包围盒树构造方法，使用上述方法可以快速生成有序的路径切点序列，但是上述切片层路径是直接将有序切点连接形成，会因三维模型数据文件的缺陷等原因，造成切面层路径不够光滑。Bezier曲线具备光滑连接特性，被广泛应用于自由曲线曲面造型中[9-10]。本文使用三次Bezier曲线来生成3D打印中切面层路径。

1 Bezier曲线的定义

Pi(i=0,1,2,…,n)是曲线的n+1个控制点，n次Bezier曲线函数的表达式为：

(1)

式中，控制点Pi决定Bezier曲线具体走向；Bi,n(u)则是n次Bernstein基函数：

(2)

2 基于Bezier曲线的路径规划

2.1 计算Bezier曲线的控制顶点

在3D打印中，每一个切片层的分层路径是与其他层路径不相交的闭合曲线。为了光滑分层路径，本文采用闭合曲线方程。首先通过切片算法得到路径切点，切点是分层路径上的点，而Bezier曲线的求解是通过确定控制顶点来完成的，所以需要先计算出Bezier曲线的控制顶点。

根据每两个顶点作为一个Bezier曲线的端点(即起始点和终止点)，并由这两个顶点结合相邻的其他两个顶点求得和这两个顶点对应的Bezier曲线的控制点，然后根据端点和控制点绘制一条过两个顶点的Bezier曲线。

如果把三阶Bezier曲线(见图1)中的P0和P3视为原始数据，只要找到P1和P2两个点(称其为控制点)，就可以根据三阶Bezier曲线公式计算出P0和P3之间平滑曲线上的任意点。

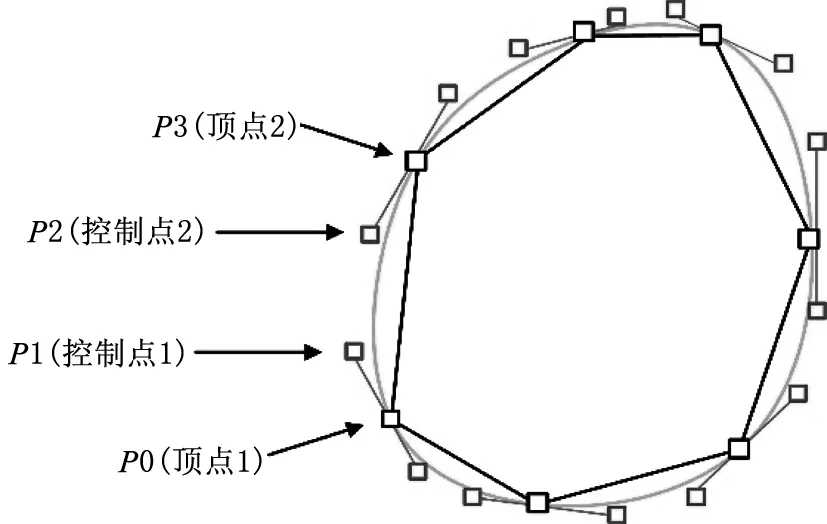
图1 三阶Bezier曲线图

所以平滑问题变成了如何计算2个原始数据点之间的控制点的问题。步骤如下。

1)第1步：粗直线连接图2中相邻的原始数据点P0、P1、P2、P3，计算出各线段的中点(Ai)，细直线连接相邻的中点。

图2 原始数据点线段中点图

需要计算P1(x1,y1)和P2(x2,y2)之间的控制点，P0(x0,y0)是前一个需要经过的点，P3(x3,y3)是下一个需要经过的点，A0(xc1,yc1)、A1(xc2,yc2)、A2(xc3,yc3)表示点与点之间连线的中点。可用代码表示为：

double xc1 = (x0 + x1) / 2.0;double yc1 = (y0 + y1) / 2.0;

double xc2 = (x1 + x2) / 2.0;double yc2 = (y1 + y2) / 2.0;

double xc3 = (x2 + x3) / 2.0;double yc3 = (y2 + y3) / 2.0;

2)第2步：根据图3中相邻2条粗直线长度之比，也就是L1/L0=d1/d0这个比例，分割其中点之间细直线连线，标记分割点。计算位于Ai连接线段上面的Bi。

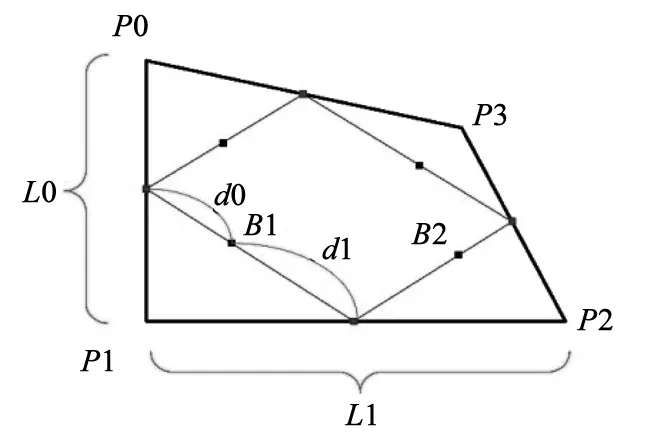
图3 分割点标记图

k1、k2表示线段比例，B1(xm1,ym1)、B2(xm2,ym2)表示中点连线上的比例分割点。代码表示为：

double len1 = sqrt((x1-x0) * (x1-x0) + (y1-y0) * (y1-y0));

double len2 = sqrt((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));

double len3 = sqrt((x3-x2) * (x3-x2) + (y3-y2) * (y3-y2));

double k1 = len1 / (len1 + len2);double k2 = len2 / (len2 + len3);

double xm1 = xc1 + (xc2 - xc1) * k1;double ym1 = yc1 + (yc2 - yc1) * k1;

double xm2 = xc2 + (xc3 - xc2) * k2;double ym2 = yc2 + (yc3 - yc2) * k2;

3)第3步：平移细直线连线，使其分割点B1、B2与相对的原始数据点P1、P2重合，得到中点连线平移图(见图4)。

图4 中点连线平移图

4)第4步：调整平移后细直线连线的端点与原始数据点的距离，通常缩减40%～80%，本文缩减50%，效果如图5所示。

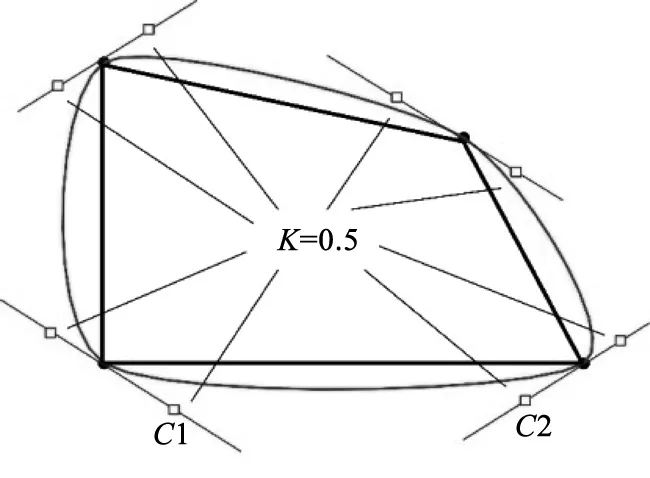
图5 端点调整图

C1(ctrl1_x, ctrl1_y)、C2(ctrl2_x, ctrl2_y)表示最后得到的控制点，smooth_value表示平滑值K，取值[0,1]。代码表示为：

ctrl1_x = xm1 + (xc2 - xm1) * smooth_value + x1 - xm1;

ctrl1_y = ym1 + (yc2 - ym1) * smooth_value + y1 - ym1;

ctrl2_x = xm2 + (xc2 - xm2) * smooth_value + x2 - xm2;

ctrl2_y = ym2 + (yc2 - ym2) * smooth_value + y2 - ym2;

使用上述方法，在切片过程中得到m+1个闭合数据点Pi(i=0,1,…,m)。本文平滑值K取为0.5，在经过控制顶点计算之后得到2m+2个控制顶点Ci(i=0,1,…,2m+1)。

2.2 求解Bezier曲线并光滑路径

经典的n次Bernstein基函数是由n+1个n次多项式函数构成的线性无关的函数组，用Bn,i(t)来表示其中的第i个，则

(3)

式中，i=0,1,…,n；t∈[0,1]。

每一个n次的Bernstein基函数都可以用2个相邻的n+1次Bernstein基函数的线性组合来表示，即Bernstein基函数具有升阶公式

(4)

式中，i=0,1,…n。

有了Bernstein基函数，并且给定了控制顶点以后，就可以用这两者的线性组合来定义Bezier曲线。这里用Qi(i=0,1,…,n)来表示n次Bezier曲线的控制顶点，用pn(t)表示n次Bezier曲线，则

(5)

由式5可知，Bezier曲线由控制顶点和Bernstein基函数共同确定，又由于曲线中所采用的Bernstein基函数的次数取决于控制顶点的数量，而一旦次数确定，Bernstein基函数便固定下来，因此可以说，Bezier曲线的形状是由控制顶点唯一确定的。

本文在平面描述中采用有序插入点策略，设定特定的步长决定曲线的疏密程度，从而表示一条在二维切面层的曲线。在Bezier曲线的每个分段上求解一定数目点的坐标，加入到路径切点坐标中的相应位置中，然后顺序连接切点生成路径。

3 试验与验证

3.1 设备情况

课题组自主开发的微喷射3D打印设备如图6所示。该设备主要由4部分组成，分别是铺粉机构、粘结剂喷射机构、机械运动机构和控制系统[11-12]。控制系统又分为硬件系统和软件系统两部分。

图6 3D打印设备

3.2 试验所用材料

试验打印的三维模型为一个齿轮，试验采用FZR-10型号的纯氧化锆陶瓷粉末，粉末的粒度控制在1 μm左右。

3.3 结果分析

使用连续打印模式，采用0.1 mm的层间距，每层打印3次。打印成形的样品如图7所示。

图7 齿轮样品

总的来说，成形样品的表面轮廓清晰，成形精度较高，能够看出轮廓曲线整体的光滑。但由于粘结剂黏度的不足，相对应粘结区域黏度不够造成部分脱落而导致极少数位置存在小缺口，而由于喷射装置电动机存在起骤停，产生抖动造成极少量毛刺。

4 结语

本文针对微喷射3D打印中分层路径粗糙问题，提出使用三次Bezier曲线优化路径形成的方法，首先通过二维切面的有序切点求出Bezier曲线控制顶点，然后根据所求得控制顶点确定Bezier曲线的基函数从而求得确定的Bezier曲线。采用有序插入点策略，设定特定的步长决定曲线的疏密程度，在曲线所经切点之间求解一定数目的顶点，加入到路径切点原始序列的相应位置，顺序连接从而表示一条在二维切面层的Bezier曲线。该方法能够使原本粗糙的切面路径变得光滑。