有理二次Bézier形式共轭双曲线段的几何计算
沈莞蔷, 汪国昭
(1. 江南大学理学院,江苏 无锡 214122;2. 浙江大学数学系,浙江 杭州 310027;3. 浙江大学CAD&CG国家重点实验室,浙江 杭州 310027)
有理二次Bézier形式共轭双曲线段的几何计算
沈莞蔷1, 汪国昭2,3
(1. 江南大学理学院,江苏 无锡 214122;2. 浙江大学数学系,浙江 杭州 310027;3. 浙江大学CAD&CG国家重点实验室,浙江 杭州 310027)
考虑有理二次Bézier形式的相互共轭的双曲线的控制顶点之间的关系,给定表示一段双曲线的标准型有理二次Bézier曲线,目标是求出它的共轭双曲线上相应段的控制顶点。首先给出共轭双曲线段的自然定义;接着通过参数变换,将有理二次Bézier形式和一般参数形式进行转换,并把这种转换对应到矩阵,以给出所求控制顶点的显式表达;最后,给出表达式的几何意义,即共轭双曲线段的控制顶点可由原双曲线的控制顶点通过两次线性插值得到。
曲线造型;有理二次Bézier曲线;双曲线;共轭双曲线;线性插值
在计算机辅助设计中,Bézier曲线及其有理模型有着良好的几何性质,常被用于数据的插值[1]、拟合[2]、逼近[3],从而被广泛用于公路设计[4]、机器人运动[5]等领域。双曲线是经典的圆锥曲线之一,被广泛用于建筑施工[6]、生态系统[7]、地质勘探[8]等领域。在所有Bézier模型中,能表示双曲线的最简单的是有理二次,其几何性质已经得到了广泛深入的研究。文献[9-10]分别研究了参数的几何意义和优化方法,文献[11]给出了圆锥曲线的几何元素(顶点、焦点等)关于有理二次Bézier控制顶点和权因子的显式表达,文献[12]给出离心率的统一表达。
然而,对有理二次Bézier形式的双曲线而言,它的共轭双曲线的表达形式还未有研究。本文将考虑有理二次 Bézier形式共轭双曲线的控制顶点之间的关系。与文献[13]不同,本文不计算双曲线的实虚轴顶点、焦点等几何元素,而是通过矩阵变换直接给出共轭后的控制顶点关于原曲线控制顶点的显式表达,并给出控制顶点的几何计算方法。
任一有理二次 Bézier曲线可以化为如下标准型[14]:

其中,参数 t∈ [0,1],权因子 ω> 0。由于有理二次Bézier曲线的三个控制顶点必定共面,且不考虑退化到单点和直线的情况,因此,不妨假设式(1)中的控制顶点pi=(xi, yi) (i=0, 1, 2)不共线。于是,当 ω<1, ω=1, ω>1时, p (t)分别为椭圆、抛物线和双曲线[15]。
除去退化到单点和直线段的情况,当权因子ω>1时,式(1)表示一段双曲线。本文考虑其共轭双曲线。在几何中,无限延伸的共轭双曲线的意义明确。然而,在计算机辅助设计中,给出的往往是双曲线的某段,它对应着共轭双曲线中的某段,本文简称共轭段。本文将先给出共轭段的自然定义,再研究式(1)的共轭段的有理二次 Bézier形式。据此,任意给定一条非退化且满足 ω>1的有理二次Bézier曲线式(1),依次提出如下两个问题:
问题 1. 给出其共轭双曲线段的控制顶点的表达式,将共轭段表示为有理二次Bézier曲线的形式;
问题2. 给出表达式的几何意义,即将共轭段的控制顶点表示为式(1)的控制顶点的线性插值形式。
1 共轭段控制顶点的显式表达
本节将先给出共轭段的自然定义,再对其控制顶点进行求解。
1.1 共轭段
对于任意双曲线,取其中心为原点,实轴顶点和虚轴顶点所在直线分别为x轴和y轴。于是,在该坐标下,该双曲线某分支(不妨假设为右支)上任意一段可表示为:

其中,a和b分别为实、虚半轴。
如图 1所示,其中红色和紫色分别表示原双曲线的右支和左支,其共轭双曲线的上、下支分别为蓝色和绿色,它们共有的两条渐近线用黑色点划线表示。参数式(2)所对应的是原双曲线右支中的某段,它用红色实线表示。式(2)所对应的左支中的段为

即为图中紫色实线段,它与红色实线段关于原点(双曲线的中心)呈中心对称。共轭双曲线的上支和下支中的相应段为:
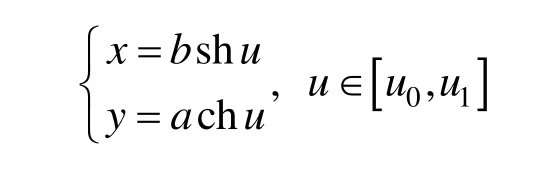
和
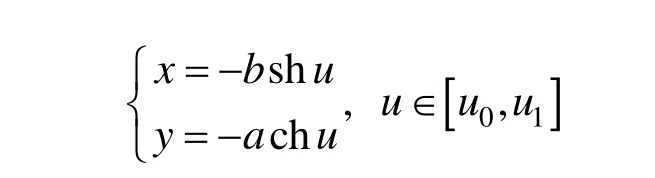
分别用蓝色和绿色实曲线段表示,它们都是式(2)的共轭段,这是一个自然的定义。

图1 双曲线共轭段的解释
至此,上节中的问题 1可以进一步明确为:若已知红色实曲线段的有理二次 Bézier标准形式如式(1),求其两共轭段(蓝色和绿色实曲线段)的有理二次Bézier标准形式。根据权因子的几何意义[16],共轭段的权因子也是ω,因此,关键是求共轭段的控制顶点。
由于有理 Bézier曲线的形状与所取坐标系无关,因此,本文考虑更一般的参数形式:
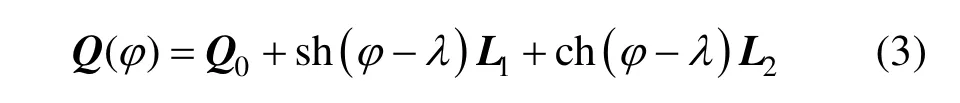
1.2 共轭段控制顶点的显式表示
根据1.1节的分析,本文希望将表示双曲线的有理二次Bézier的标准形式(如式(1)),通过参数变换,先化为类似式(3)的形式,再在其中交换中心指向虚、实轴顶点的向量,最后通过逆变换回到标准形式的有理二次 Bézier曲线,即得到原曲线的共轭段。在参数变换过程中,控制顶点的变化可用矩阵表示,逆变换对应逆矩阵,这就是本文的核心思想。其中,不需要特意求出双曲线的实虚轴顶点、焦点等几何元素。
因此,关键是要确定使用怎样的参数变换。本文从比式(3)更简单的形式入手,对于一段双曲线:
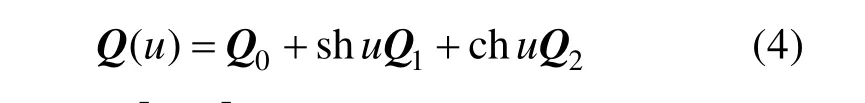
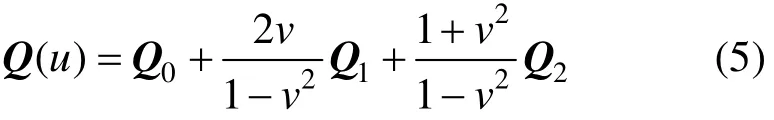
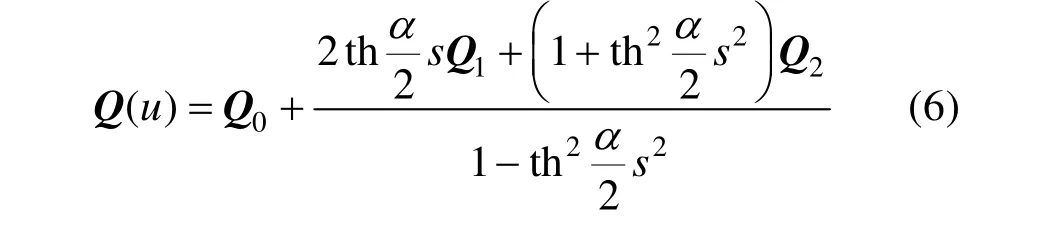

根据以上过程的逆过程,对式(1)作参数变换:
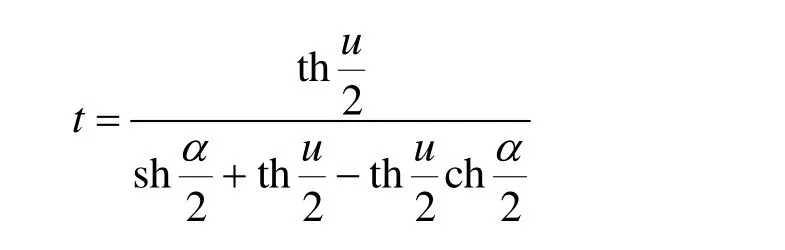
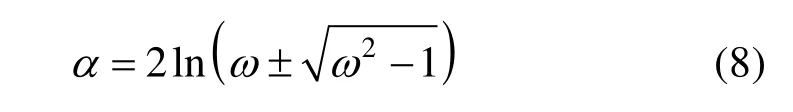
于是,式(1)化为式(4)的形式,控制顶点的关系为:
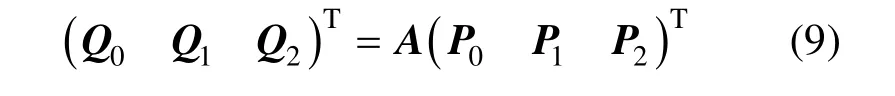
其中,A是
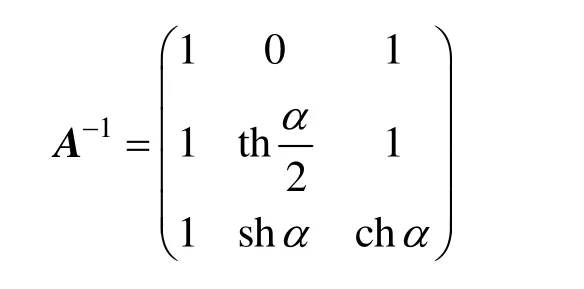
的逆矩阵:
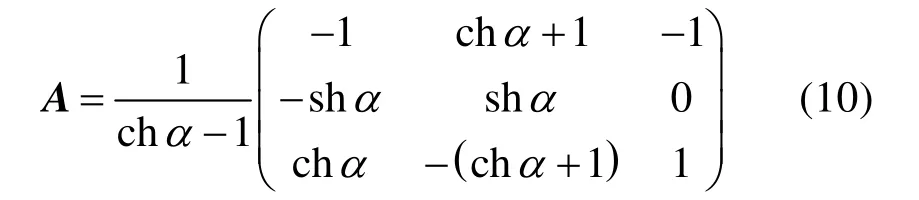
将式(4)向式(3)的形式转换,令:

使得L1和L2正交,于是有:
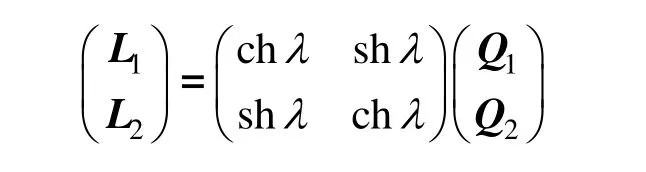
其中,
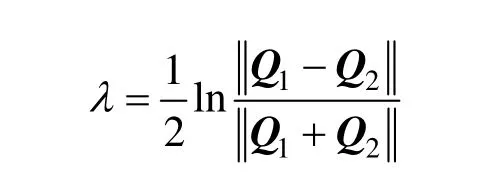
于是,得到如下关系式:
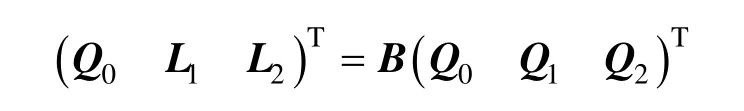
其中,
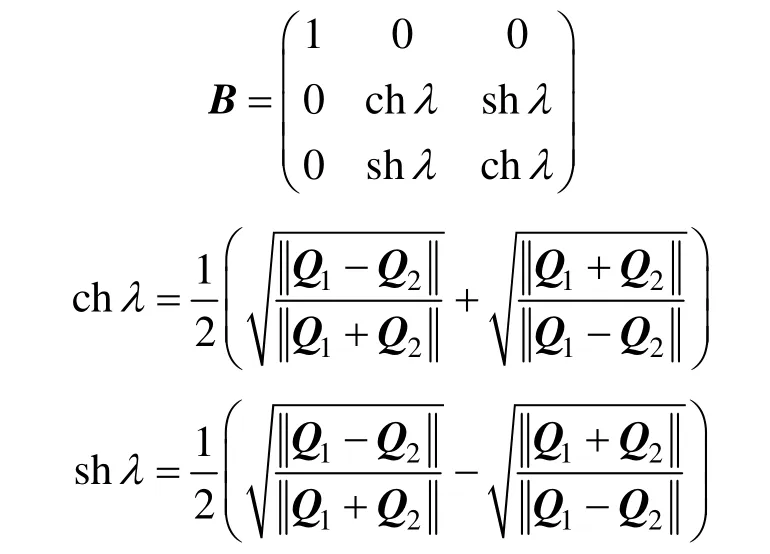
B的逆矩阵为:
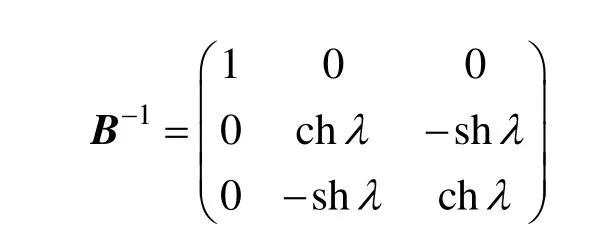
这里,L1,L2分别为双曲线中心指向虚、实轴顶点的向量,它们相交换即为共轭双曲线的中心指向虚、实轴顶点的向量。将交换矩阵设为:

记矩阵 M =A-1B-1NBA,有:
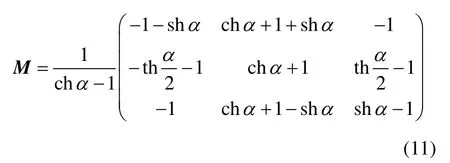
于是,得到如下定理。
定理1. (共轭双曲线段的有理二次Bézier形式)对于任意非退化的标准形式的有理二次 Bézier曲线式(1),若其表示一段双曲线(即满足 ω>1),则该双曲线的共轭段可表示为如下标准形式的有理二次Bézier曲线:
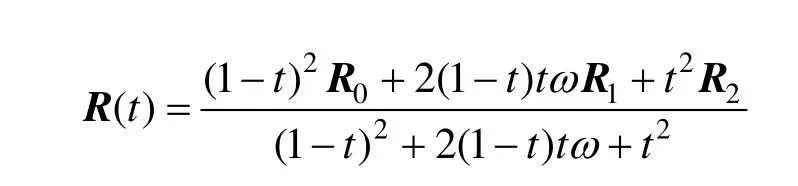
其中,控制顶点:
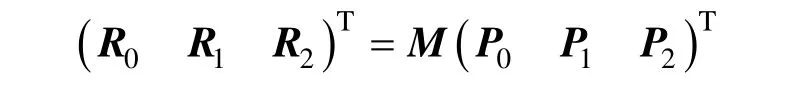
M和α分别由式(11)和式(8)给出。
在式(8)中,符号“±”代表两段共轭段。图2给出例子,ω=2。初始给定的标准型有理二次Bézier曲线,其控制顶点用红色空心圈表示,曲线用红色实线表示。其对应的另一分支上的曲线段用紫色实线表示,控制顶点用紫色空心圈表示,由原控制顶点通过双曲线的中心(即为式(9)~(10)中给出的 Q0)进行中心对称得到。由定理1给出的两段共轭段,分别用蓝色和绿色实曲线表示,它们的控制顶点,分别用蓝色和绿色空心圈表示。图2(a)是一般情况下的例子,求出的两段共轭段关于双曲线的中心呈中心对称。若给出的有理二次Bézier曲线的控制顶点构成等腰三角形则其对应的双曲线段关于实轴对称,求出的两共轭段也关于它们的实轴(即原双曲线的虚轴)对称,如图2(b)。另外,在等轴双曲线的特殊情况下,所求出的两共轭段与原给定的双曲线段分别关于两条渐近线呈轴对称,如图2(c)。

图2 求解双曲线共轭段的例子
2 几何求解
本节将指出,共轭双曲线段的控制顶点,都能表示为原双曲线段的控制顶点的线性插值(包括内插和外插)的形式,并给出实例。
在式(11)中,将矩阵M重新表示为 M =CD,其中,
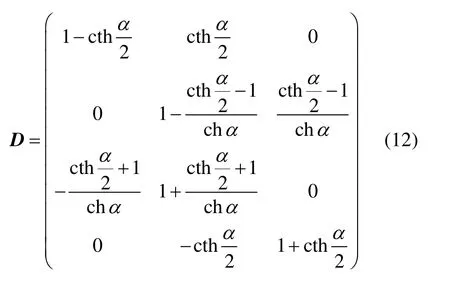
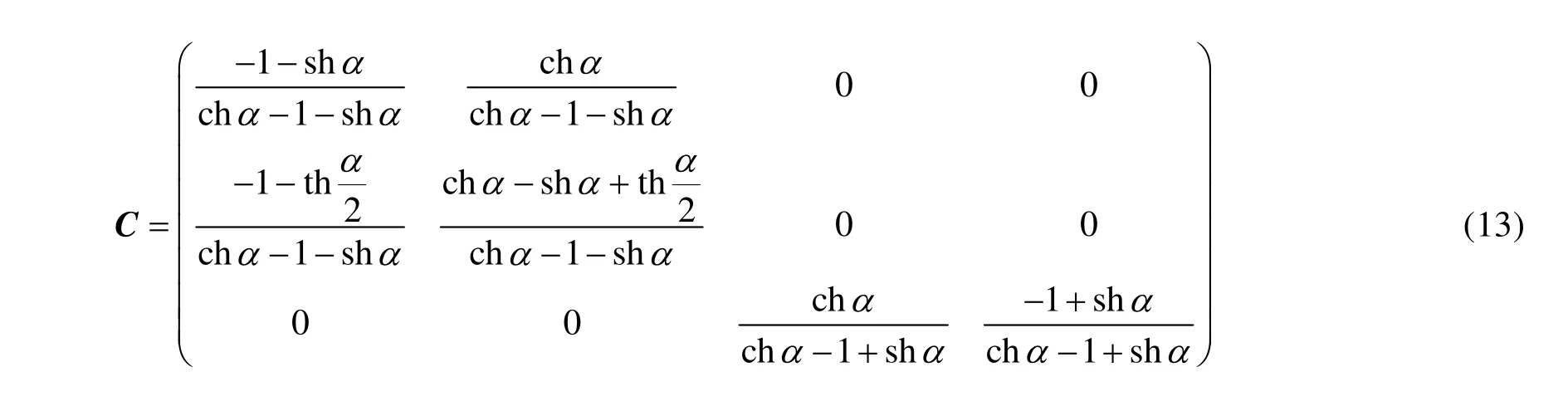
或者,
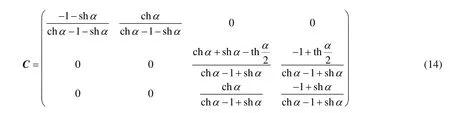
在这些矩阵中,每行仅有相邻的两个元素非零,并且它们的和均为 1,这即是线性插值的形式。假设:
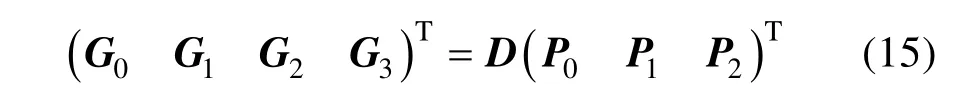
表示由原始控制顶点进行第一次线性插值所得的过渡点,于是:
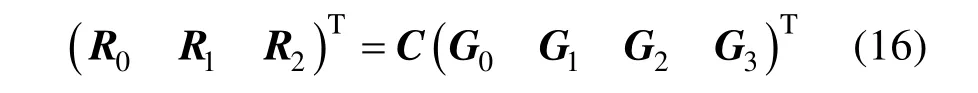
算法1. (共轭双曲线段的有理二次Bézier形式的几何求解)若给定任意表示双曲线的非退化的标准形式的有理二次Bézier曲线式(1),即已知不共线的三个控制顶点p0,p1,p2和权因子 ω>1,则其共轭段的控制顶点R0, R1, R2可以通过如下步骤求得:
(1) 根据式(8),通过权因子ω计算出α(正负号算出不同的α代表了不同的两段共轭段)。
(2) 根据式(12)和式(15),通过p0,p1,p2线性插值出过渡点G0,G1,G2,G3。
① 在p0P1上分别取的定比分点G0,G2。
② 在p1P2上 分 别 取的定比分点
(3) 根据式(13)(或式(14))和式(16),通过G0,G1,G2,G3线性插值出R0,R1,R2。
①在G0G1,G2G3上分别取的定比分点R0,R2。
②在G0G1上取的定比分点(对应式(13)),或者取的定比分点(对应式(14)),即为R1。
图3给出一个例子,ω=1.2。给定有理二次Bézier曲线的控制顶点p0,p1和p2(红色空心圈),其两共轭段的控制顶点通过p0,p1和p2的线性插值得到。蓝色和绿色共轭段的相关点分别用上标1和2来标记。对于蓝色共轭段,在式(8)中取“+”号,此时,记α=α1,中间的过渡插值点和采用蓝色实心点表示,相应共轭段的控制顶点和采用蓝色空心圈表示;对于绿色共轭段,在式(8)中取“–”号,此时,记α=α2,中间的过渡插值点和采用绿色实心点表示,相应共轭段的控制顶点和采用绿色空心圈表示。
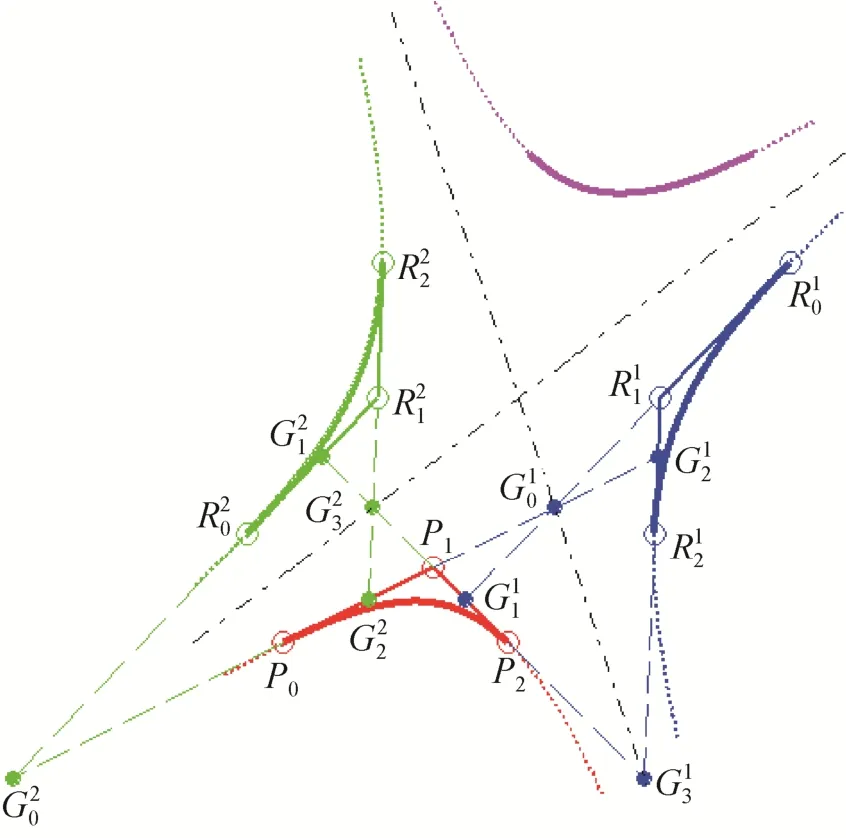
图3 双曲线共轭段的控制顶点的几何求解
3 结 论
本文针对表示双曲线的有理二次 Bézier曲线的标准型式(1),研究其共轭段的表示。先在引言中提出关于共轭段的控制顶点的显式表达的问题1,以及关于表达式的几何意义的问题 2。接着,在第1~2节中分别回答了问题1、2。今后可以对包含双曲函数的混合空间中的拟 Bézier曲线(AH Bézier[17]、AHT Bézier[18])的共轭问题进行研究,也可应用于椭圆类曲线的几何元素的求解[19]。
[1] 林建兵, 陈小雕, 王毅刚. 有理二次Bézier曲线的几何Hermite插值新方法[J]. 计算机科学与探索, 2013, 7(7): 667-671.
[2] 赵文彬, 谢晓薇, 杨福增, 等. 基于二次有理Bézier曲线拟合的颅骨识别技术研究[J]. 生物医学工程学杂志, 2008, 25(2): 280-284.
[3] Hu Qianqian. Approximating conicSections by constrained Bézier curves of arbitrary degree [J]. Journal of Computational and AppliedMathematics, 2012, 236(11): 2813-2821.
[4] Walton D J,Meek DS. G2 curve design with planar quadratic rational BézierSpiralSegments [J]. International Journal of ComputerMathematics, 2013, 90(2): 325-340.
[5] 陈 军, 王国瑾. 规避障碍物的G2连续有理二次Bézier样条曲线[J]. 计算机辅助设计与图形学学报, 2011, 23(4): 582-585.
[6] 闫宏业, 刘 莉, 廖志刚, 等. 采用改进的修正双曲线法预测高速铁路路基沉降[J]. 铁道建筑, 2011, 12: 92-94.
[7] 孙敬松, 周广胜. 基于叶面积指数改进的直角双曲线模型在玉米农田生态系统中的应用[J]. 生态学报, 2013, 33(7): 2182-2188.
[8] 施 剑, 吴志强, 崔三元, 等. 南黄海盆地地震勘探中的非双曲线时差分析[J]. 石油地球物理勘探, 2013,48(2): 192-199.
[9] Hu Qianqian, Wang Guojin. GeometricMeanings of the parameters on rational conicSegments [J].Science in ChinaSeries A:Mathematics, 2005,48(9): 1209-1222.
[10] Isabelle C H, Gudrun A, VictoriahM. Optimal parameterization of rational quadratic curves [J]. Computer Aided Geometric Design, 2009, 26(7): 725-732.
[11] Lee E T Y. The rational Bézier representation for conics [C]//Farin G E. GeometricModeling: Algorithms and New Trends, vol 14. Philadelphia:Society for Industrial and AppliedMathematics Publications, 1987: 3-19.
[12] Xu Chengdong, Kim T W, Farin G. The eccentricity of conicSections formulated as rational Bézier quadratics [J]. Computer Aided Geometric Design, 2010, 27(6):458-460.
[13] 沈莞蔷, 汪国昭. 线性双曲拟Bézier曲线的几何图形[J]. 计算机工程与应用, 2014, 50(7): 10-14,40.
[14] Farin G. Rational quadratic circles are parametrized by chord length [J]. Computer Aided Geometric Design, 2006, 23(9): 722-724.
[15] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M].北京: 高等教育出版社; 海德堡: 施普林格出版社, 2001: 35-43.
[16] 施法中. 反求标准型有理二次Bézier曲线的参数与内权因子[J]. 计算机辅助设计与图形学学报, 1995, 7(2): 91-95.
[17] Li Yajuan, Wang Guozhao. Two kinds of B-basis of the algebraic hyperbolicSpace [J]. Journal of Zhejiang UniversityScience A, 2005, 6(7): 750-759.
[18] Xu Gang, Wang Guzhao. AHT Bézier curves and NUAHT B-spline curves [J]. Journal of ComputerScience and Technology, 2007, 22(4): 597-607.
[19] 沈莞蔷, 汪国昭, 徐红林. 线性p-Bézier曲线的几何形状[J]. 计算机辅助设计与图形学学报, 2014, 26(8): 1211-1218.
Geometric Calculation of Conjugate HyperbolaSegment Presented as Rational Quadratic Bézier Form
Shen Wanqiang1, Wang Guozhao2,3
(1.School ofScience, Jiangnan University, Wuxi Jiangsu 214122, China; 2. DepartmentofMathematics, Zhejiang University, Hangzhou Zhejiang 310027, China; 3.State Key Laboratory of CAD & CG, Zhejiang University, Hangzhou Zhejiang 310027, China)
Consider the relationship between the control points of the conjugate hyperbolas presented as rational quadratic Bézier forms. Given a rational quadratic Bézier curve withStandard form presenting a hyperbolicSegment, the target is to calculate the control points of the correspondingSegment on its conjugate hyperbola. Firstly, the natural definition of theSegment of conjugate hyperbola is given.Secondly, parameter conversion is used to transform the hyperbola between the rational quadratic Bézier form and a general parametric form. The transformations correspond toMatrices. Thus the explicit expressions of the control points of the conjugateSegments are obtained. Finally, the geometricMeanings of the expressions areShown. Each control point of the conjugate hyperbolaSegments can be given by two linear interpolations of the control points of the original hyperbolaSegment.
curveModeling; rational quadratic Bézier curve; hyperbola; conjugate hyperbola; linear interpolation
TP 391.72
A
2095-302X(2015)02-0172-06
2014-10-08;定稿日期:2014-10-24
国家自然科学基金资助项目(11326243,61402201,61272300,11371174);江苏省自然科学基金青年基金资助项目(BK20130117)
沈莞蔷(1981–),女,江苏无锡人,讲师,博士。主要研究方向为计算机辅助几何设计、计算机图形学。E-mail:wq_shen@163.com

