DP基关于L2内积的对偶函数及其应用

蔡华辉， 彭永康， 柳炳祥

(景德镇陶瓷学院信息工程学院，江西 景德镇 333403)

DP基关于L2内积的对偶函数及其应用

蔡华辉， 彭永康， 柳炳祥

(景德镇陶瓷学院信息工程学院，江西 景德镇 333403)

给出DP基关于L2内积对偶函数的显示表示公式。首先介绍了计算机辅助几何设计中多项式对偶函数的一般理论；然后根据两组多项式基的转换公式，给出了相应对偶函数的转换公式。随后利用此转换公式和Bernstein基对偶函数的表示公式，推导出DP基关于L2内积对偶函数的显示表示。讨论了对偶函数在计算机辅助几何设计中的应用。

DP基；对偶函数；L2内积；广义De Boor-Fix公式；逼近

在计算机辅助几何设计(computer aided geometric design, CAGD)中，自由曲线曲面的表示经常利用控制顶点与相应基函数的乘积和来实现。由于不同的基函数具有不同的特性，所以由其构造的曲线也会有相应的特性。因此，为了满足不同设计需求，提出用多种曲线表示的方法，其中在CAGD领域中最为常用的多项式曲线是利用Bernstein基表示的Bézier曲线[1]。除此之外，Sánchez-Reyes[2]为了克服幂基和Hermite插值多项式的缺点利用对称幂基表示多项式曲线，王国瑾[3]与Said[4]分别借助三次Ball曲线提出了Wang-Ball曲线和Said-Ball曲线，Wu[5]利用增加位置参数的方法，进一步推导得到了两类广义 Ball曲线，即Wang-Said 型 广 义 Ball (Wang-Said type generalized Ball, WSGB)曲线与Said-Bézier型广义Ball (Said-Bézier type generalized Ball,SBGB) 曲线，汪志华和朱晓临[6]利用类似方法，定义了Wang-Bézier 型 广义 Ball (Wang-Bézier type generalized Ball, WBGB)曲线，沈莞蔷和汪国昭[7]通过加入多个参数也构造了一类广义 Ball曲线。Delgado和Peña[8]在2003年也提出了一类新的多项式曲线表示方法，即DP曲线，它既拥有Bézier曲线的保形性，又拥有广义Ball曲线的计算效率。

在曲线曲面逼近等应用中，对偶函数是一类有效的工具。关于多项式基的对偶函数的讨论在CAGD中有2类。

第1类是利用加权 L2内积获得。令Pn是次数不超过n的多项式构成的 n+1维实线性空间，定义加权L2内积：

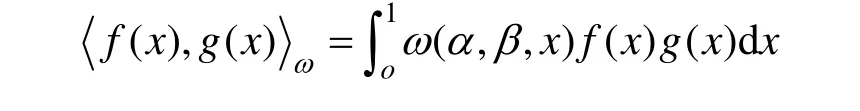
式中，f(x)，g(x)是pn中的任意多项式，ω(α,β,x)是在上的Jacobi权函数。

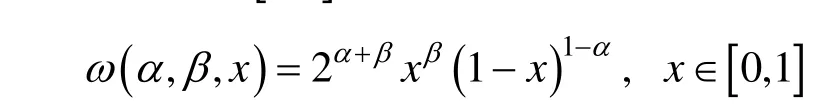
若在pn上存在两组基和满足：

则可在pn的对偶空间pn*中定义线性算子：

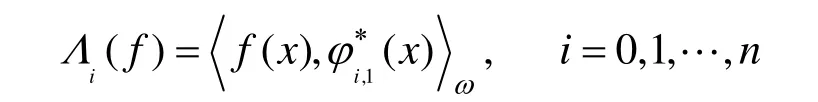
第2类是利用广义De Boor-Fix公式获得。令f(x)， g(x)是 pn中的任意多项式，定义广义 De Boor-Fix公式[12]：

式中，右边是与τ无关的常量。若存在 pn上的两组基满足：

则在 pn的对偶空间 pn*中定义线性算子：

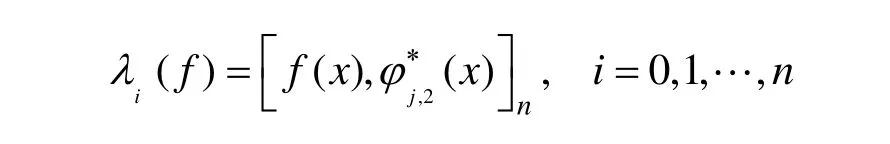
成立。奚梅成[13]与Othman和Goldman[14]各自独立得到了Said-Ball基的对偶基，Wu[15]讨论了SBGB基的对偶基，Jiang等[16]得到了WSGB的对偶基，Zhang等[17-18]分别讨论了对称幂基和WBGB基的对偶基。

DP曲线方面，尽管许多学者对其与Bézier曲线的相互转换[19-20]和曲线降阶算法[21-22]等进行了广泛讨论，但对 DP基的对偶函数还没有加以研究。为了便于求解任意曲线的最佳逼近DP曲线，本文研究DP基关于L2范数对偶函数的显示表示。

1 两组基与对偶基的关系

利用已知多项式基的对偶函数讨论另一组多项式基的对偶函数是一种获得对偶函数显示表示的常用方法。因此，首先给出两组基和对偶基之间的一个基本定理。

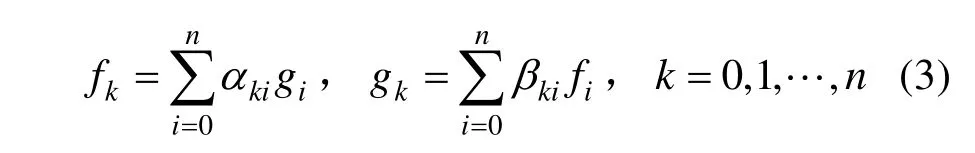
则对偶函数满足：

证明. 设μjkvjk分别是和两组基转换公式的系数，即满足：

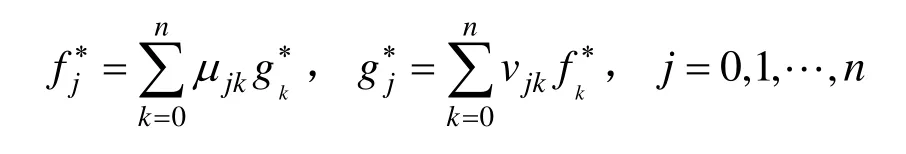
要证明定理1，即要证明系数满足：

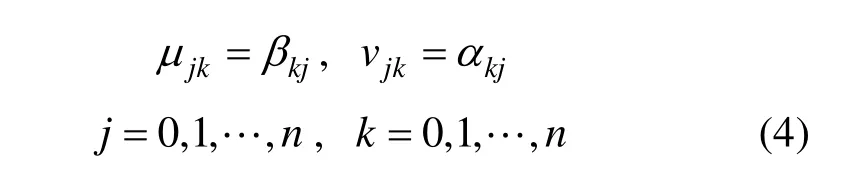
由式(3)，得：

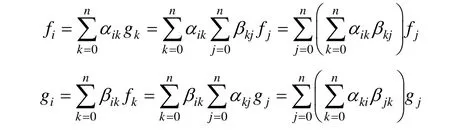
利用上面两式可得：

利用式(1)、(3)和(4)，可得：

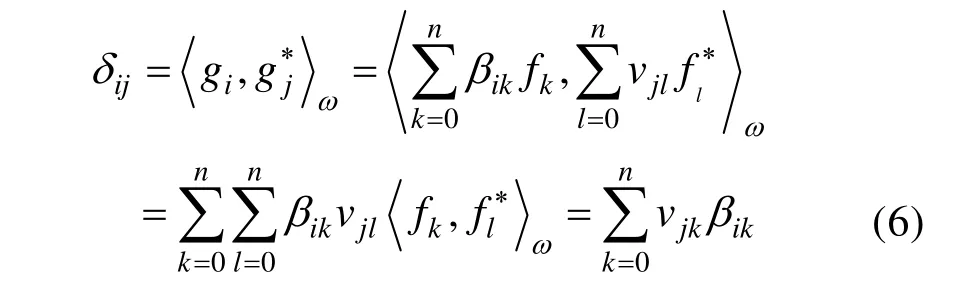
再利用式(5)~(6)，可得：

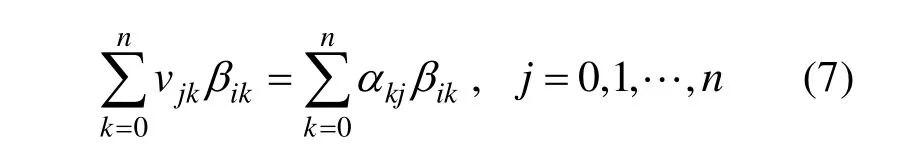
实质上，利用定理1的方法可以证明关于广义De Boor-Fix公式的对偶函数也满足定理1的结论。下面就利用定理1和Bernstein基的相应结论给出DP基关于L2内积对偶函数的显示表示。

2 DP基关于L2内积的对偶函数

以pi(i=0,1,…,n)为控制顶点的n次DP曲线[8]：

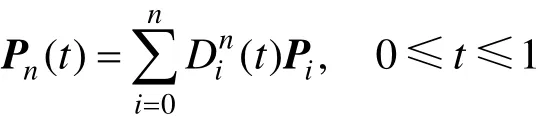
式中：

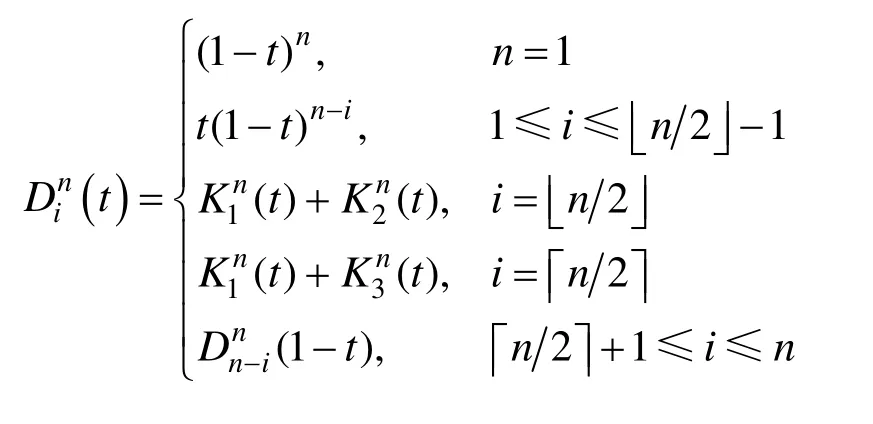
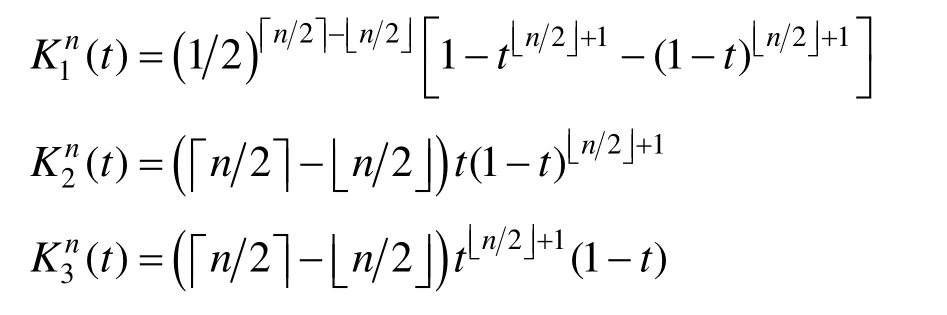
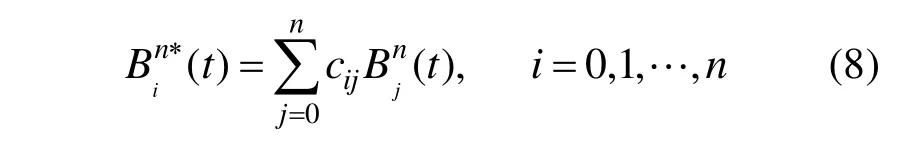
式中：

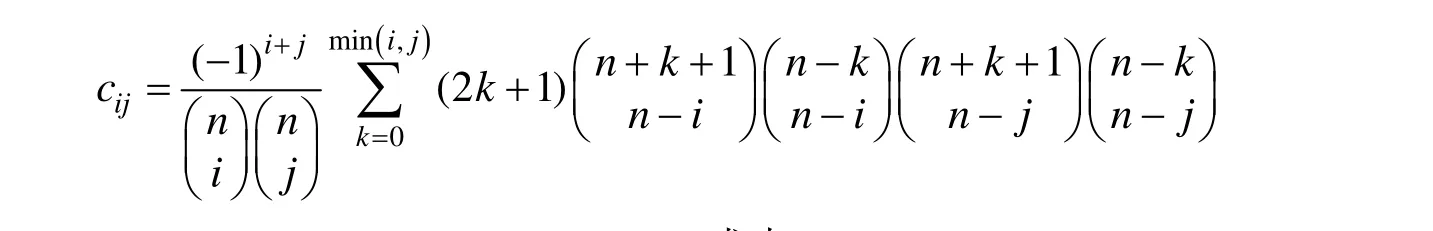
为了利用定理 1，还需要知道 Bernstein基到DP基的转换公式，文献[20]给出了相应转换公式。

分别是Bernstein基到DP基，则：

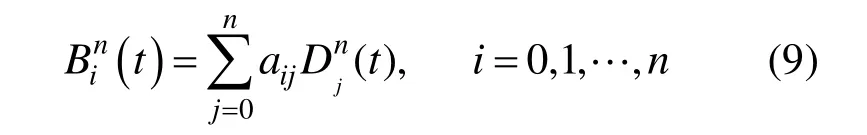
当n为偶数时：

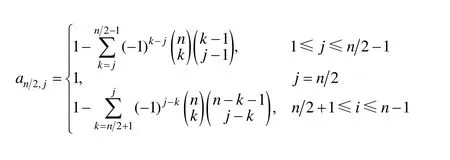
式中：

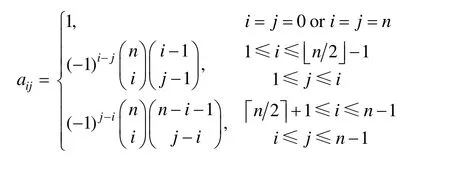
当n为奇数时：

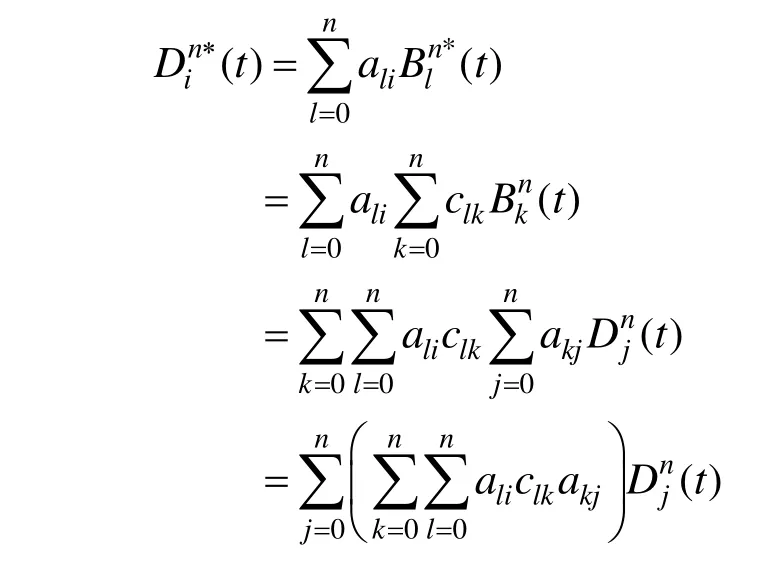
因此，可以得到如下定理。

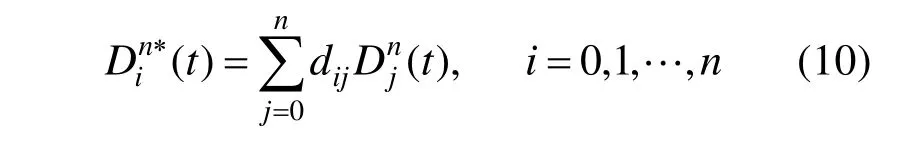
式中：

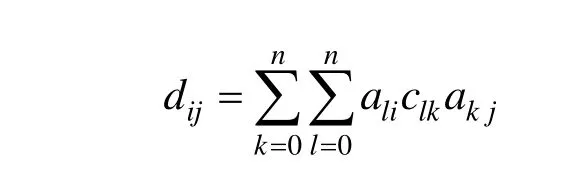
其中，aij和cij(i, j=0,1,… ,n)分别有式(8)~(9)给出。

当 n=3时，利用定理2，可以得到三次DP基的对偶函数的表达式：

图1给出了三次DP基和对偶基的实例。图1(a)是三次DP基：图1(b)是关于L2范数的对偶函数：

实质上利用定理1和Bernstein基也非常容易得到其他多项基关于加权L2内积对偶函数的显示表示，如文献[11]利用构造两个向量内积矩阵的方法得到的WBSG基关于加权L2内积的对偶函数，证明过程繁琐，利用本文定理 1也可以得到相同的结论。

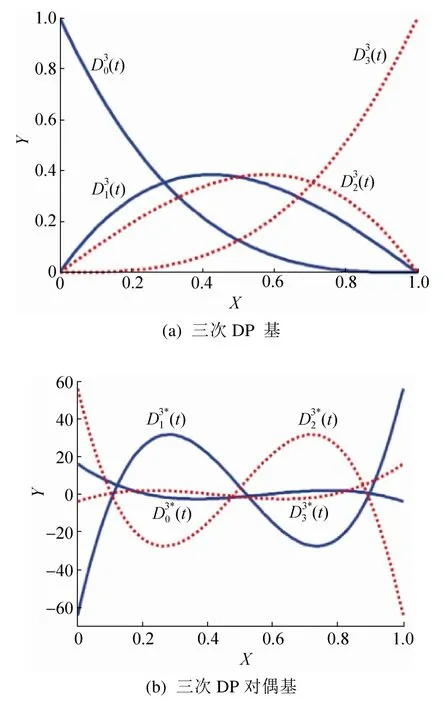
图1 三次DP基和对偶基实例

3 任意曲线的DP曲线逼近

给定任一函数 p(t),寻求 p(t)的最佳多项式逼近是CAGD中的一个基本问题确定了DP基的对偶函数后，寻求 p(t)最小平方逼近意义下的最佳DP多项式是非常容易的。

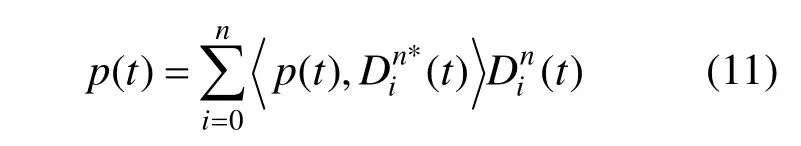
证明. 不妨设函数 p(t)的n次DP逼近多项式为：

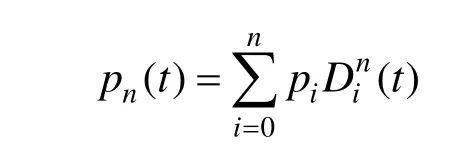
由于pn(t)是 p(t)关于L2范数的最小平方逼近，因此要满足：

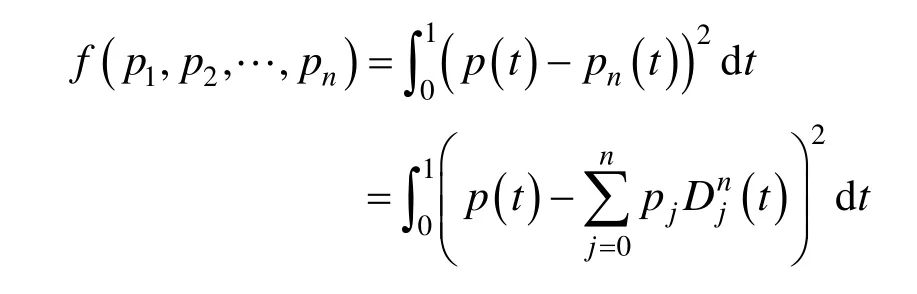
极小。对上式中的 pi ,(i=0,1,… ,n)求偏导，应满足：

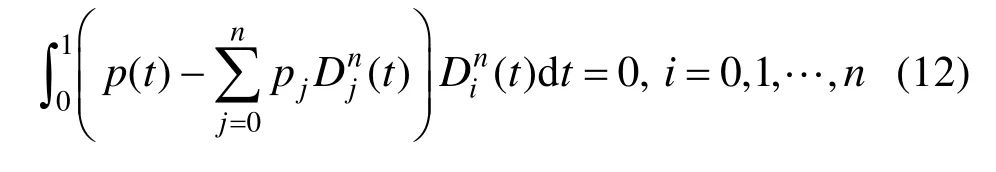
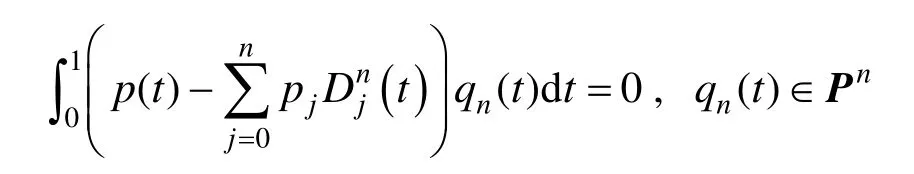
由上式，可知：

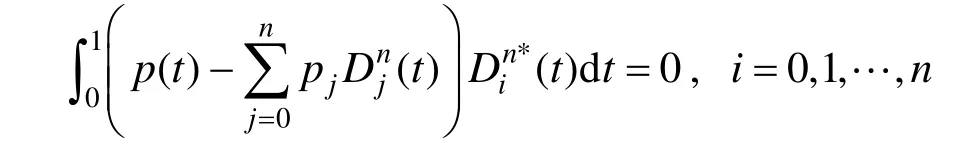
可得：

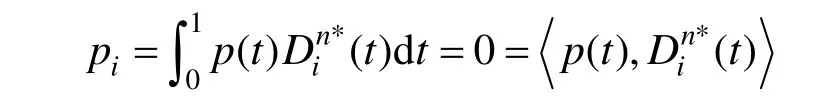
即，可证定理3。

由于圆弧不能精确表示为多项式曲线，给出圆弧的多项式逼近表示是非常重要的，例如圆弧：

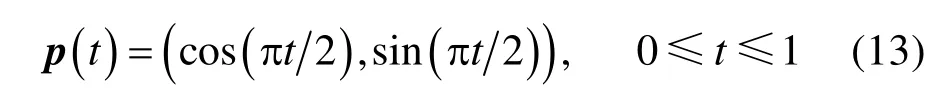
利用式(11)，分别对x和y分量求得三次 DP曲线逼近控制顶点依次为(0.9973,–0.0023), (1.4926, 0.0553), (0.0553, 1.4926), (–0.0023, 0.9973)，逼近结果如图2所示。

4 结 束 语

本文介绍了CAGD领域中的两类多项式对偶函数, 并给出了两组多项式基和对偶基之间满足的相互关系。在此基础上，给出了 DP基关于L2范数对偶函数的显示表示，同时把对偶函数用于任意曲线的最小平方逼近问题。但是，在对偶函数的显示表示式(10)中 dij计算复杂，且在曲线逼近应用中没有考虑端点约束，因此，如何简化 dij计算和利用对偶函数获得满足端点约束的最佳逼近DP曲线是今后必须研究的重要问题。

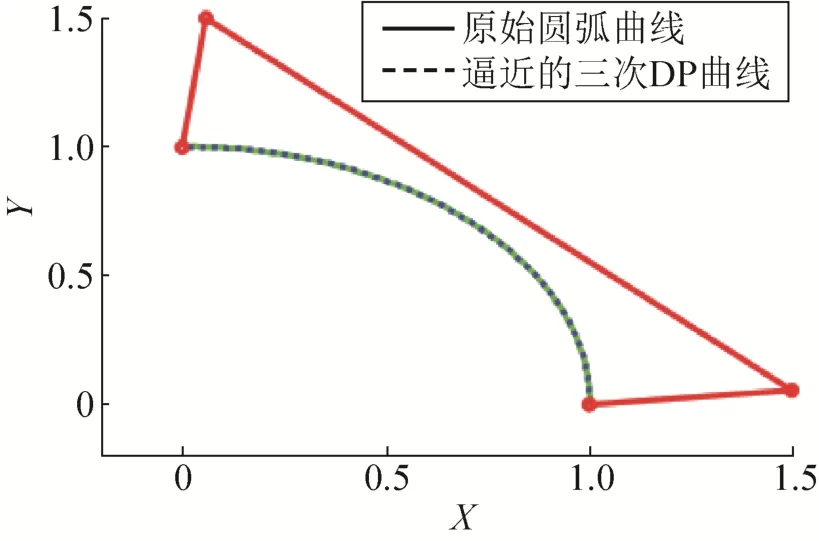
图2 圆弧及其三次逼近DP曲线

[1] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M].北京: 高等教育出版社, 2001: 18-33.

[2]Sánchez-Reyes J. TheSymmetric analogue of the polynomial power basis [J]. ACM Transactions on Graphics, 1997, 16(3): 319-357.

[3] 王国瑾. 高次Ball曲线及其几何性质[J]. 高校应用数学学报, 1987, 2(1): 126-140.

[4]Said H B. A generalized Ball curve and its recursive algorithm [J]. ACM Transactions on Graphics, 1989, 8(4): 360-371.

[5] Wu Hongyi. Unifying representation of Bézier curve and generalized Ball curves [J]. AppliedMathematics-A Journal of Chinese Universities, 2000, 15(1): 109-121.

[6] 汪志华, 朱晓临. Bézier曲线与Wang-Ball曲线的统一表示[J]. 计算机辅助设计与图形学学报, 2008, 20(7): 888-893.

[7] 沈莞蔷, 汪国昭. 一类新的广义Ball基及其相应曲线[J]. 浙江大学学报: 工学版, 2011,45(3):435-439.

[8] Delgado J, Peña JM. AShape preserving representation with an evaluation algorithm of linear complexity [J]. Computer Aided Geometric Design, 2003, 20(1): 1-20.

[9] Jüttler B. The dual basis functions for the Bernstein polynomials [J]. Advances in ComputationalMathematics, 1998, 8(4): 345-352.

[10] Rababah A, Al-NatourM. The weighted dual functional for the univariate Bernstein basis [J]. AppliedMathematics and Computation, 2007, 186(2): 1581-1590.

[11] Zhang Li, Tan Jieqing, Wu Hongyi, et al. The weighted dual functions for Wang-Bézier type generalized Ball bases and their applications [J]. AppliedMathematics and Computation, 2009, 215(1): 22-36.

[12] Goldman R N. Dual polynomial bases [J]. Journal of Approximation Theory, 1994, 79(3): 311-346.

[13] 奚梅成. Ball基函数的对偶基及其应用[J]. 计算数学, 1997, 19(2): 147-153.

[14] Othman W A N, Goldman R N. The dual basis functions for the generalized Ball basis of odd degree [J]. Computer Aided Geometric Design, 1997, 14(6): 571-582.

[15] Wu Hongyi. Dual bases for a new family of generalized Ball bases [J]. Journal of ComputationalMathematics, 2004, 22(1): 79-88.

[16] Jiang Pin, Wu Hongyi, Tan Jieqing. The dual functionals for the generalized Ball basis of Wang–Said type and basis transformation formulas [J]. NumericalMathematics, A Journal of Chinese Universities (EnglishSeries), 2006, 15(3): 248-256.

[17] Zhang Li, Wu Hongyi, Tan Jieqing. Dual basis functions for the NS power and their applications [J]. AppliedMathematics and Computation, 2009, 207(2):434-441.

[18] Zhang Li, Wu Hongyi, Tan Jieqing. Dual bases for Wang–Bézier basis and their applications [J]. AppliedMathematics and Computation, 2009, 214(1): 218-227.

[19] JiangSurong, Wang Guojin. Conversion and evaluation for two types of parametricSurfaces constructed by NTP bases [J].Mathematical and ComputerModelling, 2005,49(2-3): 321-329.

[20] 成 敏, 王国瑾. 均匀 B 样条基与 DP-NTP 基之间的转换与应用[J]. 软件学报, 2006, 17(增刊): 38-45.

[21] Aphirukmatakun C, Dejdumrong N.Multiple degree elevation and constrainedMultiple degree reduction for DP curves andSurfaces [J]. Computers andMathematics with Applications, 2011, 61(8): 2296-2299.

[22] Liu Gang, Wang Guojin. Optimal constrained explicitMulti-degree reduction approximation of DP curves [J]. Journal of Information and ComputationalScience, 2011, 8(6): 869-876.

Dual Functions onL2Inner Product for DP Basis and Their Applications

Cai Huahui, peng Yongkang, Liu Bingxiang
(School of Information Engineering, Jingdezhen Ceramic Institute, Jingdezhen Jiangxi 333403, China)

An explicit formula for the dual functions of DP basis onL2inner product is derived. The general theory of polynomial dual functions in computer aided geometric design is first introduced, and by using conversion formulas between two polynomial basis, the conversion formulas between two corresponding dual functions are deduced. Then with this conversion formulas and the dual functions of Bernstein basis, the dual functions of DP basis onL2inner product are obtained. Finally, the application of this result in computer aided geometric design is discussed.

DP basis; dual functions;L2inner product; generalized De Boor-Fix formula; approximation

TP 391

A

2095-302X(2015)02-0166-06

2014-10-08；定稿日期：2014-10-24

国家自然科学基金资助项目(61262038, 61164014)；江西省自然基金资助项目(2012BAB201044)；景德镇市科技局资助项目

蔡华辉(1975–)，男，浙江东阳人，副教授，博士。主要研究方向为计算机辅助几何设计、计算机图形学。E-mail：huahuicai@gmail.com