2个随机量子比特混合态内积的概率密度函数

黄金萍，张 林，王子嫣

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

随机矩阵理论或概率论是研究量子信息理论的有力工具。近年来，量子信道容量的非可加性猜想被随机矩阵理论工具破解，证明了量子纠缠可以提高量子信道容量[1]。对一般的多体随机量子态，Duistermaat-Heckman测度被用于刻画其单体约化密度矩阵的特征值的联合概率分布密度以及特征值的联合分布[2-5]。随机矩阵理论还可用于分析可观测量的不确定性关系和量子测量的不相容性，例如，文献[6]研究了d维空间中的2组量子测量联合可测的刻画，并将量子测量随机化，运用概率等相关理论研究了二维空间上的2组无偏测量的不相容概率。在计算测量不相容概率的过程中，文献[6]用到2个实单位矢量内积的概率密度函数。类似地，文献[7]中提及到复的单位矢量内积的模的平方被称为转移概率，文献[8]研究了2个复的单位矢量(对应于纯态)的内积的模的概率密度函数，受文献[6]和文献[8]的启发，本文计算2个随机量子混合态内积的概率密度函数，并给出2个随机量子比特混合态内积的概率密度函数的精确表达式。

1 预备知识

定义1[9]δ函数的定义为：

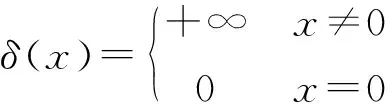
用傅里叶积分表示为：

其中，i是虚数单位。

符号函数sgn定义如下：

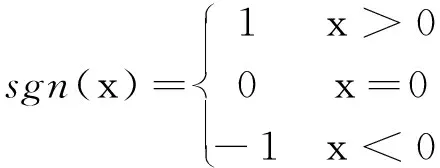
引理1[10](HCIZ积分公式) 设A和B是n×n自伴矩阵，其特征值分别满足λ1(A)<λ2(A)<…<λn(A)和λ1(B)<λ2(B)<…<λn(B)。记

则积分公式

2 主要结果

设ρ,σ∈D(Cn)，2个随机混合量子态的内积r=〈ρ,σ〉的概率密度函数pn(r)为[6]：

(1)

当n=2时，得出以下解析结果。

定理2个随机混合量子态ρ,σ∈D(C2)内积的概率密度函数为：

用δ函数的积分表示为：

其中，α为一变量。

由引理1和式(1)可得：

令

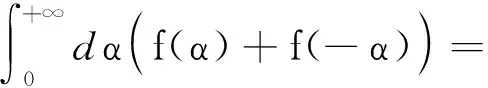
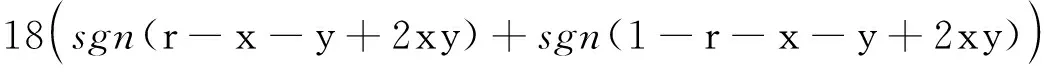
最后，使用Mathematica计算推导得到：

接下来，考虑r,1-r,x+y-2xy的大小关系。

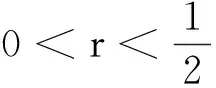
sgn(r-x-y+2xy)+sgn(1-r-x-y+2xy)=2或0或-2，只有

sgn(r-x-y+2xy)+sgn(1-r-x-y+2xy)=2时有意义，此时

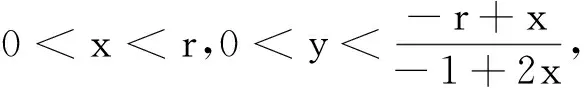
sgn(r-x-y+2xy)+sgn(1-r-x-y+2xy)=2或0或-2，只有

sgn(r-x-y+2xy)+sgn(1-r-x-y+2xy)=2时有意义，此时

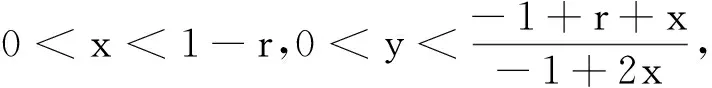
因此，得到：

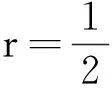
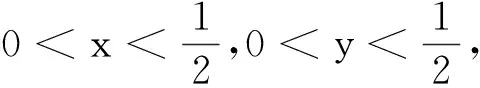
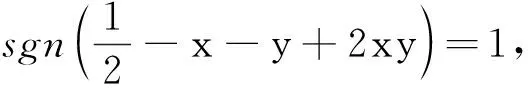
此外，计算得出：

最后，借助数学软件Mathematica，得到2个随机量子比特混合态内积的概率密度函数的具体图像如图1所示。

图1 2个随机量子比特混合态内积的概率密度函数

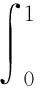
3 结束语

已发表文献中，在研究随机量子测量的联合可测概率时，仅考虑实或复的随机纯量子态内积的概率密度两种情形。本文考虑随机混合量子态内积的概率密度函数情形，计算出随机量子比特混合态内积(作为一维随机变量)的概率密度函数，并得到精确的函数解析式和对应的概率密度函数图，在不确定性关系研究中具有潜在应用。由于高维空间中的量子比特内积的概率密度函数计算的复杂性，下一步将寻找其它方法来研究高维空间中量子比特内积的概率密度函数。