基于DTW距离的探地雷达数据可视化

段丽丽， 原 达， 能昌信

(1. 山东师范大学信息科学与工程学院，山东 济南 250014；2. 山东省高校智能信息处理重点实验室，山东工商学院，山东 烟台 264005)

基于DTW距离的探地雷达数据可视化

段丽丽1， 原 达2， 能昌信2

(1. 山东师范大学信息科学与工程学院，山东 济南 250014；
2. 山东省高校智能信息处理重点实验室，山东工商学院，山东 烟台 264005)

提出一种基于动态时间弯曲算法距离度量的探地雷达数据可视化方法，利用动态时间弯曲算法在时间轴方向上伸缩的优越性，结合可指定类数的聚类算法对探地雷达数据进行聚类和可视化分析。可用于实测的探地雷达数据集，实验结果表明，相对于传统的聚类算法，本文算法能得到更好的聚类结果。

k-means；动态时间弯曲算法；探地雷达数据；可视化

探地雷达(ground penetrating radar, GPR)作为一个非常重要的遥感工具，是近几年适应快速、准确地无损探测地下障碍物以及对地下工程评价而迅速发展起来的新技术。在土木工程、地雷探测和环境应用等领域中，运用GPR探测地下埋藏物或非均匀介质一直是被关注的话题。

与一般的成像方法不同，GPR成像是电磁波经过反射、相干和叠加后得到的地下介质间接表示。电磁波在地下的传播过程十分复杂，各种噪声和杂波的干扰非常严重，使得探测回波数据伴有多种杂波和相干噪声。地质雷达噪声信号的影响是多方面的，有收发天线件直接耦合波、空气直达波、地表反射波、介质环境反射波、噪声干扰波和目标反射波等，这些噪声和干扰波有来自环境的也有来自系统的[1]。在成像过程中，为了反映更多的反射波属性，通常采用宽频带进行记录，于是在图像中不仅含有各种有效属性，也存有各种复杂干扰波，增加了专业人员的辨识难度。

目前常用的GPR数据处理方法有滤波、反褶积、多次叠加、道均衡处理、速度分析、振幅处理技术等，其中滤波是最常用的有效手段，目的是利用频谱特性的不同来压制干扰波。雷达反射波，是由所有介质的反射响应组合而成，可以使用多种成像算法反转，例如时域标准法相投影(standard back projection,SBP)[2]、傅里叶域雷达成像技术[3]等。标准的时域和频域成像算法对数据采集过程的脉冲响应进行匹配滤波，以形成图像。所有这些算法需要精细的空间采样和高速率的时间采样[4]。因此，GPR数据采集是地下成像过程的关键所在。现在大部分GPR处理软件的时频分析功能强大，但是数据解释能力有限。为了更好地反映GPR数据包含的特征和规律，需要对处理后的数据进行更进一步的成像处理。

在GPR成像中，使用频率分集通常可以实现良好的深度分辨率，但横向分辨率难于实现。Capineri等[5]提出了一种获得良好分辨力的 GPR成像方法，它是通过对B扫描数据应用Hough变换技术来实现的。Morrow和Van Genderen[6]通过运用反向传播和共轭梯度反演技术形成二维和三维的钻孔雷达图像，但是这些技术有很大的计算消耗。因此，Ozdemir等[7]提出了一种新的基于合成孔径雷达(synthetic aperture radar，SAR)的GPR成像算法，它能够在深度和横向方面同时达到良好分辨力。该方法使用快速傅里叶变换形成三维图像，随后从距离角度域简单变换到图像域。但是该算法在转换域时存在图像失真问题，并且假设土壤介质均匀，土壤属性为已知，具有一定的局限性。Qin和 Wang[8]提出运用基尔霍夫迁移方法来处理GPR数据，实现了对地下物体的定位和再造。虽然基尔霍夫偏移方法具有较强的能力，能输出单个或多个物体的雷达输出图像，但图像结果比较简单，并且图像解释对专业经验的要求非常高。

数据可视化的思想是运用计算机图形学和图像处理技术来表达数据，将离散的、杂乱的数据经过加工处理，利用计算机可视化提供的图像表示出来，直接观察数据中蕴涵的现象或规律，提高解释的效率、可靠性和精度[9]，以满足各行各业非专业人员的需求。探地数据可视化是探地数据解释的基础，图形能够给用户一种更直观的感受，方便用户对感兴趣的数据进行操作，帮助解释人员更好地了解地质情况[10]。常用的地质剖面显示方法有3种：波形显示、变面积显示和密度显示[11]。

本文提出一种新的基于动态时间弯曲算法(dynamic time warping, DTW)距离度量的GPR数据可视化方法，对 GPR数据进行可视化分析，在成像的基础上产生更直观有效的视觉效果，为 GPR数据的解释提供可靠的理论基础。基本思路是，首先对数据进行滤波和特征提取，然后运用DTW距离与k-means聚类相结合的方法对特征数据集进行聚类分析，最后对类别信息进行颜色映射以得到GPR数据的可视化图像(如图1所示)。

图1 可视化流程概念图

1 探地雷达波形特点

根据电磁波传播和反射理论，接收信号常常由4个部分组成：天线串扰、地面反射、目标反射和白噪声。可公式化为：。由图2可以看出，GPR回波信号具有非平稳性，脉冲信号非线性衰减等特点，图中给出的示例波形从左到右存在明显的非线性衰减的现象。

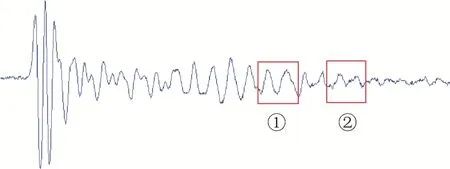
图2 探地雷达波形图示例

距离度量用于确定时间序列之间以及时间序列分类的相似性。欧氏距离是可以使用的一种有效的距离度量。两个相等长度的时间序列之间的欧氏距离是简单地从一个时间序列中的 n个点到另一个时间序列中的 n个点的距离的总和[12]。它的定义为：

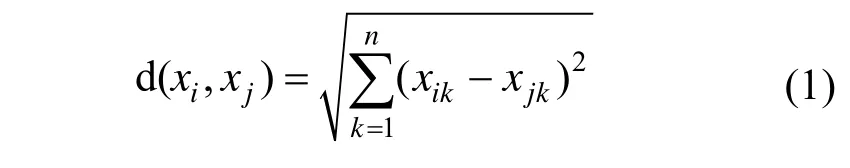
欧氏距离适合某些领域[13]，但其结果往往不直观。如图3所示，如果两个时间序列是相同的，但是一个沿时间轴稍稍错开，那么欧式距离会认为是不同的，如图2中标注的①、②两段波形。DTW 被引入来克服这个限制，忽视时间序列的时间维度的移动，并给出直观的距离测量。它能够较好地解决欧氏距离难以处理的对应数据间沿时间轴方向的伸缩、弯曲和线性漂移等问题[14]。与欧式距离相比，DTW 可以度量等长或不等长的时间序列[15]，能够实现异步相似性比较，并且DTW不满足三角不等式。由于GPR波在传播过程中会发生沿时间方向的吸收衰减，进而对应反射数据在时间轴方向上会产生压缩，因此，用DTW距离度量能更好地计算GPR时间序列之间的相似性。

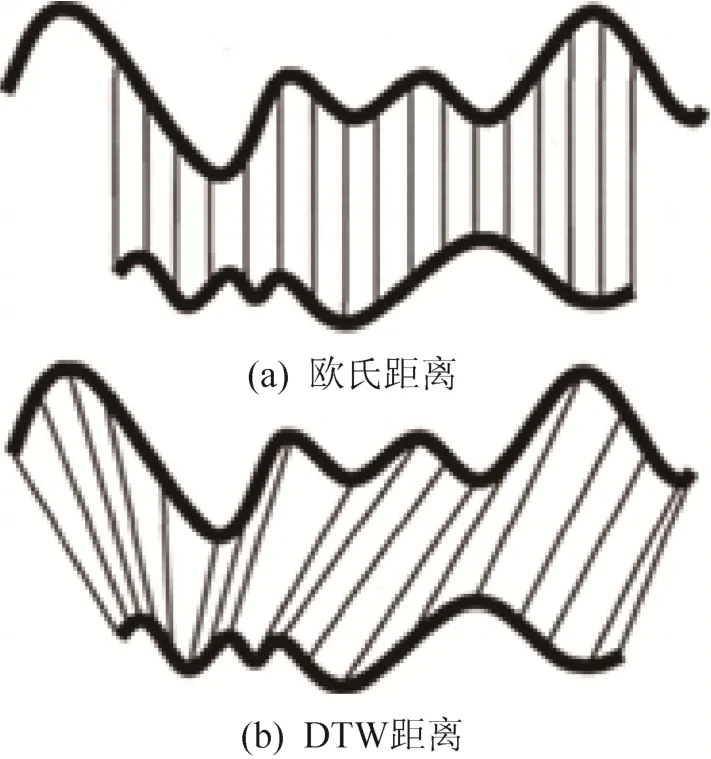
图3 欧氏距离与DTW距离比较

2 动态时间弯曲

DTW是一种通过弯曲时间轴来更好地对时间序列形态进行匹配映射的相似性度量方法。DTW距离的计算通过弯曲时间轴获取两个时间序列间的最小距离，并确定两个时间序列中各个点的最佳对应关系。该算法是要寻找一条通过各个交叉点的从起始点到终止点的最佳路径，使得该路径上所有交叉点的帧失真度总和达到最小[16]。

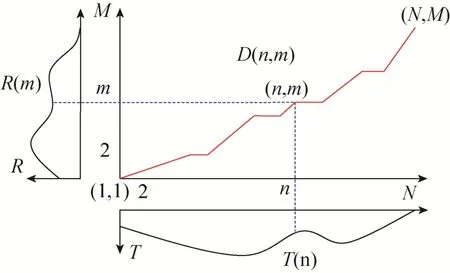
图4 DTW算法求最小弯曲距离

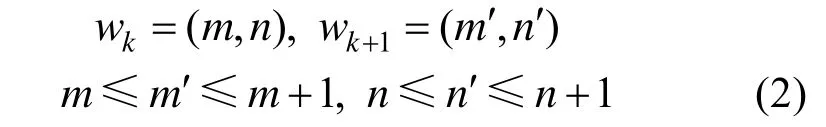
最优弯曲路径是一个具有最小距离的弯曲路径，弯曲路径W的距离是：

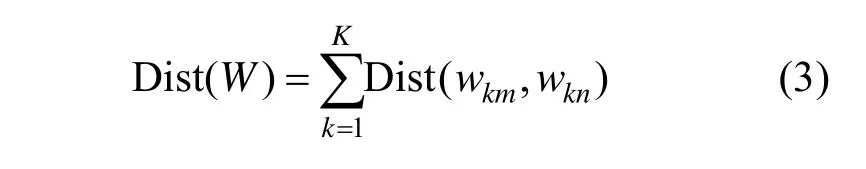
式中，Dist(wkm,wkn)是弯曲路径的第k个元素中的两个数据点(一个来自序列R，一个来自序列T)索引的距离。

采用基于累积距离矩阵的动态规划方法来计算两序列之间的最小距离的弯曲路径。一个M×N的二维距离代价矩阵 D被创建，D(m,n)的值是时间序列R′=＜R1,…,Rm＞和序列T′=＜T1,… ,Tn＞之间的最小弯曲距离。D(M,N)包含了时间序列R和T之间的最小弯曲距离。图4展示了从 D(1,1)到D(M,N)的一个最小距离弯曲路径实例。为了找到最小距离的弯曲路径，代价矩阵的每个元素都必须被计算。构造的累积距离矩阵为：

其中，D(0,0)=0，D(m,0)=D(0,n)=+∞。

到 D(m,n)的变形路径必须通过相邻的三个元素之一，由于它们之间的弯曲距离是已知的，所有这一切需要的是加当前两点之间的距离Dist(m,n)到这三个邻近元素的最小值上。代价矩阵从下到上、从左向右填充。因此，整个矩阵填充后，能找到一条从D(1,1)到D(M,N)的弯曲路径。

3 基于DTW距离的聚类

本文提出了一种改进的基于 DTW 距离的GPR数据可视化模型，算法步骤如下：

(1) 对给定数据集Data，进行滑动窗口均值滤波处理，得到数据集D，表示为：

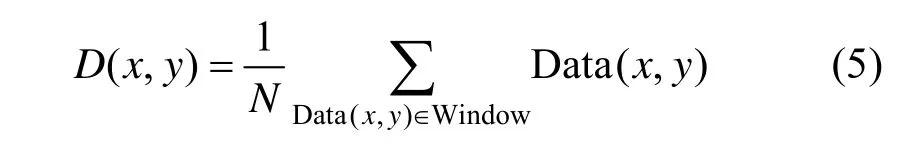
其中，Window表示滑动窗口，N表示窗口中像素的总个数。

(2) 对数据集 D中的每个元素提取特征向量Pi，1≤i≤row(D)column(D)，则：

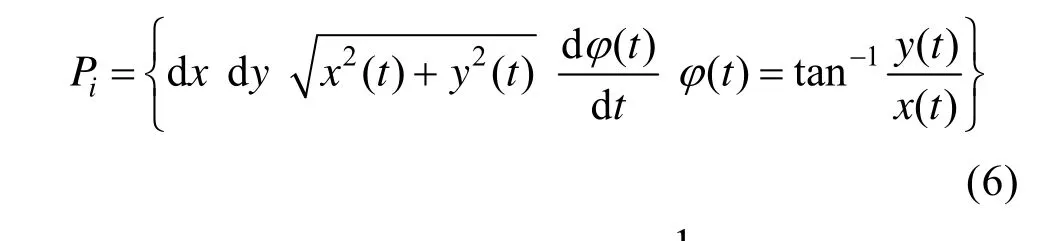
(3) 在特征集P中，任意指定k个初始聚类中心cj，1≤j≤k，设定迭代次数t=0。

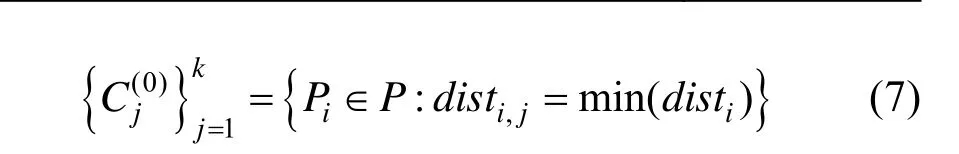
(5) 更新每个簇的聚类中心：

其中，nj是簇 Cj中向量的总个数。

(6) 如果：

收敛或达到指定迭代次数，输出类别矩阵；否则，转到步骤(4)。

(7) 对类别矩阵进行颜色映射，最终得到数据集的可视化成像。

4 实验结果及分析

实验使用真实数据集进行分析。所用数据由1 238道数据组成，每道数据由240字节道头和道数据组成，采样点个数为2 048(如图5所示)。

首先，对原始数据进行滤波预处理。通过比较各种尺寸窗口的滤波效果，选择效果较好的参数来对GPR数据进行处理，本实验经验选取较优的大小为 7×7的滑动窗口滤波，用幅值彩色成像来对比滤波前后效果，如图6所示。

由图5和图6的初始成像效果可以观察到，图像右下方的数值范围比较密集，在灰度图中区分度很小，而幅值直接映射图中，图像右下方有了较为明显的类别区分。

由于GPR波在地下的传播过程中，会随着时间的推移产生振幅衰减，但频率等特征是不会发生改变的。因此，对滤波后的数据提取多维特征p(如图7)，得到的样本总数为2042×1232，且每个样本的特征向量的维数为5，并用k-means聚类对数据进行无监督聚类处理。经过多次实验选定 k值为5和7，并同时对两种方法进行效果比较，如图8所示。

从图8可以看出，在聚类k值相同时，本文方法比传统k-means方法具有更好的区分度，聚类效果更符合预期的结果。在k值为5时，两种方法对矩形框中数据的聚类结果均为 2类，但是，可以看出，传统k-means方法得到的图像有随着时间推移衰减的趋势，甚至消失，而本文的方法很好地移除了吸收衰减对成像效果的影响，成像更接近预期效果。在 k值为7时，对比图 8(c)和图 8(d)两图，发现本文提出的方法聚类更细致，能够发现数据中更多的潜在特征规律。而同时研究图8(b)和图8(c)，可以推出，对数据集矩形框区域的数据，传统k-means聚7类与k-means-DTW聚5类的效果是几乎一致的。因此，无论是在精细度还是抗衰减方面，本文提出的k-means-DTW聚类均优于传统的基于欧氏距离的k-means聚类，并且实验验证了所提方法的有效性。

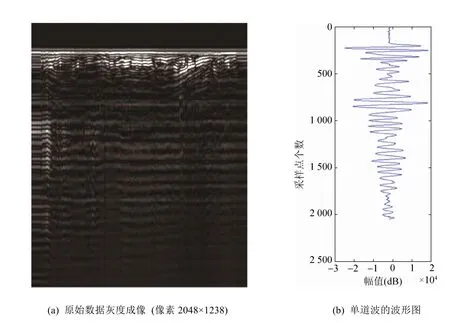
图5 原始数据成像及单道波形图

图6 对原始数据依据幅值进行颜色映射

图7 特征向量p={横向梯度，纵向梯度，瞬时幅值，瞬时频率，瞬时相位}

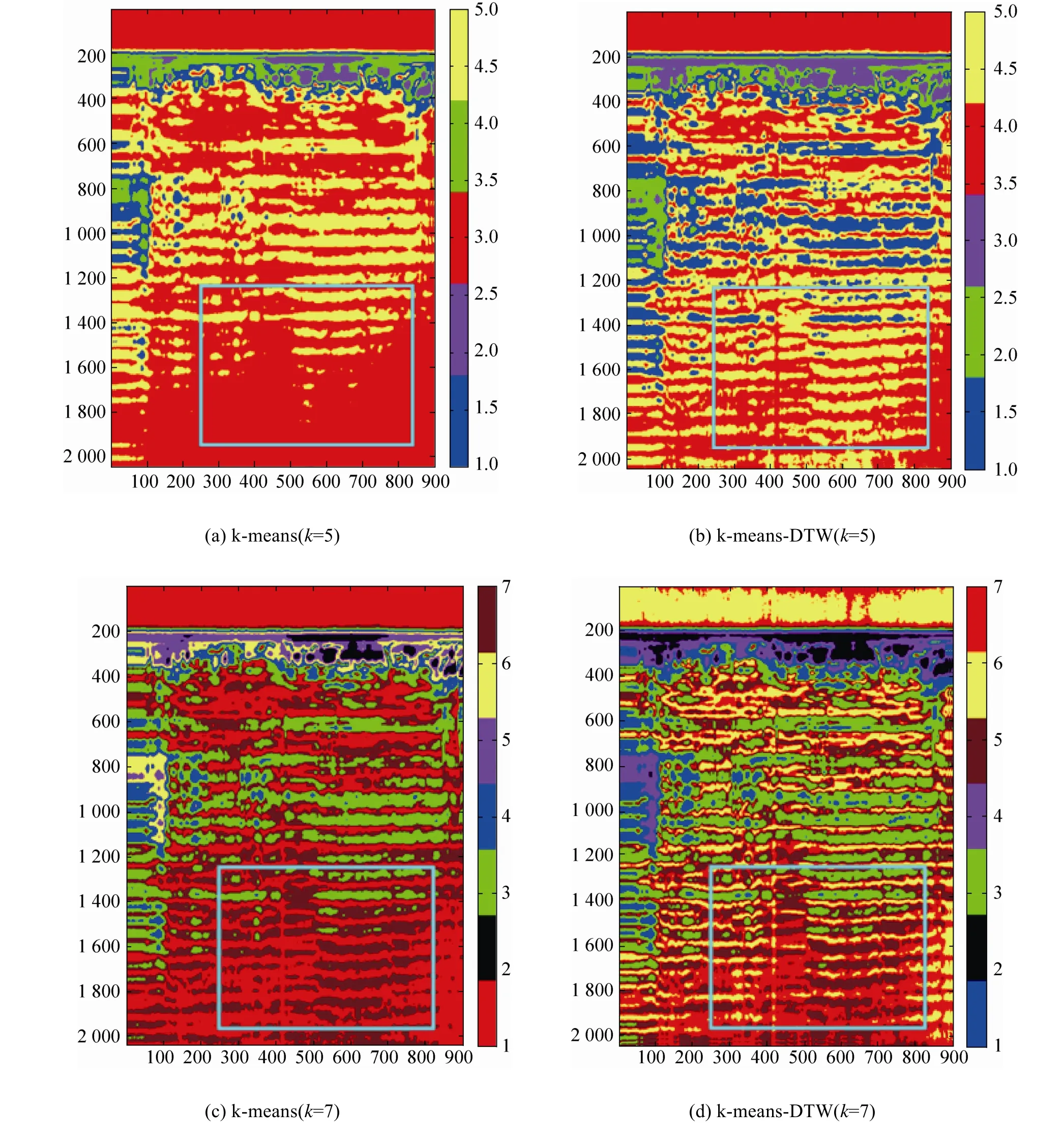
图8 两种方法实验结果对比

5 结 论

本文提出一种新的基于 DTW距离的动态相似性度量方法，并结合指定类数的聚类算法对GPR数据进行聚类并可视化分析。处理了数据在时间轴方向上的伸缩和平移问题，一定程度上克服了信号随时间衰减对可视化结果的影响。将本文算法应用于真实的GPR数据集，并与传统方法进行对比，结果表明本文方法可以挖掘到更多的GPR数据规律。在今后的工作中，将结合多种算法进一步研究GPR数据的多方面的属性展示。

[1] 张永山. 探地雷达异物目标探测与数据处理研究[D].太原： 中北大学, 2012.

[2] Feng Xuan,SatoM. Pre-stackMigration applied to GPR for landmine detection [J]. Inverse Problems, 2004, 20(6) 99-115.

[3]Stolt R H.Migration by Fourier transform [J]. Geophysics, 1978,43(1)： 23-48.

[4] Gurbuz A C,McClellan J H,Scott W R. CompressiveSensing for GPR imaging [C]//The41stAsilomar Conference onSignals,Systems and Computers. Pacific Grove, USA, 2007： 2223-2227.

[5] Capineri L, Grande P, Temple J A G. Advanced image‐ processing technique for real‐ time interpretation of ground ‐penetrating radar images [J]. International Journal of ImagingSystems and Technology, 1998, 9(1)： 51-59.

[6]Morrow I L, Van Genderen P. A 2-D polarimetric backpropagation algorithm for ground ‐penetrating radar applications [J].Microwave and Optical Technology Letters, 2001, 28(1)： 1-4.

[7] Ozdemir C, LimS, Hao Ling. ASynthetic‐aperture algorithm for ground‐penetrating radar imaging [J].Microwave and Optical Technology Letters, 2004,42(5)：412-414.

[8] Qin Yao, Wang Qifu. Kirchoff migration algorithm for ground penetrating radar data [C]//ComputerScience and Electronics Engineering (ICCSEE), 2012 International Conference on IEEE. Hangzhou, 2012：396-398.

[9] 张二华, 高 林, 马仁安, 等. 三维地震数据可视化原理及方法[J]. CT理论与应用研究, 2007, 16(3)：20-28.

[10] 蔡维纬. 二维地震数据可视化的研究与实现[D]. 昆明：云南大学, 2013.

[11] 肖 汉. 地震数据的可视化技术研究[D]. 长沙： 湖南大学, 2007.

[12]SalvadorS, Chan P. Toward accurate dynamic time warping in linear time andSpace [J]. Intelligent Data Analysis, 2007, 11(5)： 561-580.

[13] Keogh E, KasettyS. On the need for timeSeries dataMining benchmarks： a survey and empirical demonstration [J]. DataMining and Knowledge Discovery, 2003, 7(4)： 349-371.

[14] 程文聪, 邹 鹏, 贾 焰, 等. 基于DTW距离的伪周期数据流异常检测[J]. 计算机研究与发展, 2010,47(5)： 893-902.

[15] 陆薛妹, 胡 轶, 方建安. 基于分段极值DTW距离的时间序列相似性度量[J]. 微计算机信息, 2007, 23(9-3)：204-206.

[16] 王 倩, 吴国平, 陈 琳. 特定人语音识别算法——DTW算法[J]. 软件导刊, 2005, (20)：46-48.

Ground Penetrating Radar Data Visualization Based on Dynamic Time Warping

Duan Lili1, Yuan Da2, Nai Changxin2
(1.School of InformationScience and Engineering,Shandong Normal University, JinanShandong 250014, China; 2. Key Laboratory of Intelligent Information Processing in Universities ofShandong,Shandong Institute of Business and Technology, YantaiShandong 264005, China)

In this paper, we propose a visualizationMethod of ground penetrating radar data based on dynamic time warping distanceMetric, which uses the advantages of dynamic time warping algorithm on the time axisScaling, and combines with theSpecified clustering algorithm for ground penetrating radar data clustering and visualization analysis. The algorithm is used for theMeasured ground penetrating radar dataSets; the experimental resultsShow that compared with the traditional clustering algorithm, the proposed algorithm can get better clustering results.

k-means; dynamic time warping; ground penetrating radar data; visualization

TP 391

A

2095-302X(2015)02-0152-07

2014-10-08；定稿日期：2014-10-30

国家自然科学基金资助项目(61373079)

段丽丽(1989–)，女，山东潍坊人，硕士研究生。主要研究方向为可视化与图像处理。E-mail：duanlili.123@qq.com通讯作者：原 达(1968–)，男，辽宁建昌人，教授，博士。主要研究方向为可视化与图像处理。E-Mail：ydccec@126. com