面向控制顶点优化的自由曲线交互拟合技术

蒋水秀 单 岩

1.杭州科技职业技术学院，杭州，311402 2.浙江大学，杭州，310027

0 引言

自由曲线拟合是计算机辅助几何设计（CAGD）的一项重要技术［1－3］，是自由曲面逆向建模的基础和前提，在逆向工程设计领域（如汽车设计）有广泛的应用。自由曲线的拟合效果可从两方面评估：一是拟合精度［4－8］，即点群与曲线最大偏差；二是拟合曲线的光顺性［9－10］，即要求曲线连续且没有非设计意图的波动。

在现有的曲线拟合研究及相关CAD软件中，对拟合精度的控制已经比较成熟，然而对拟合曲线的光顺性控制则缺乏有效的手段。

影响曲线光顺性的关键因素有两个：一是曲线的阶数，即控制顶点数量；二是控制顶点的分布状态。现有的自动拟合方法往往只能通过减少控制顶点数量（同时也牺牲了拟合精度）来改善光顺性，而对优化控制顶点的分布则缺乏有效手段。

曲线控制顶点的分布不仅影响曲线的光顺性，还对曲线的编辑、拼接等后续操作的方便性有重要的影响。因此，在曲线拟合中，如不能对曲线的控制顶点分布进行有效的干预，则会使曲线拟合功能的实用性大打折扣。

本文针对这一现状，提出并实现了一种新的自由曲线交互拟合方法。该方法首先通过人工交互手段，逐步增加拟合曲线控制顶点数，并调整和优化其分布状态。然后，通过对自由曲线控制顶点位置的全自动迭代调整，使曲线逼近点群，保证了拟合效率及精度。

1 交互拟合流程

如图1所示，｛p j｝（j＝1，2，…，n）是用来拟合曲线的n个有序空间点，称为型值点或拟合点，其交互拟合流程如下：

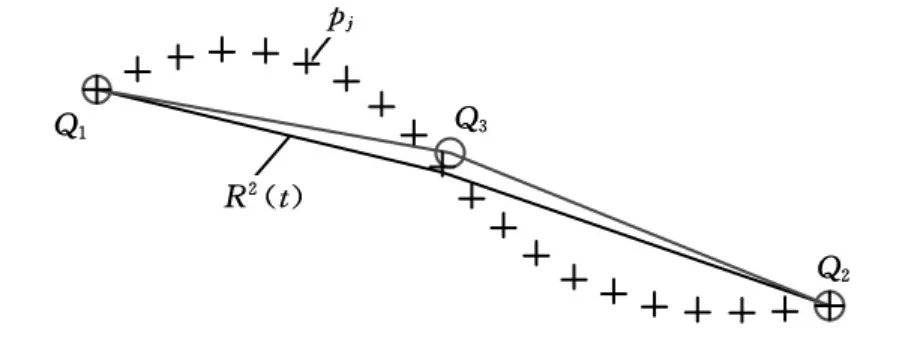
图1 初始拟合曲线

（1）创建初始拟合曲线。根据｛p j｝拟合二阶样条曲线R2（t），其两端控制顶点分别为Q1和Q2，中间控制顶点为Q3。

（2）交互增加控制顶点。根据拟合偏差情况，在合理位置交互添加第m个控制顶点Q m（m＞3），此时控制顶点数增加到m个，由这些控制顶点生成m－1次样条曲线Rm－1（t），如图2所示。

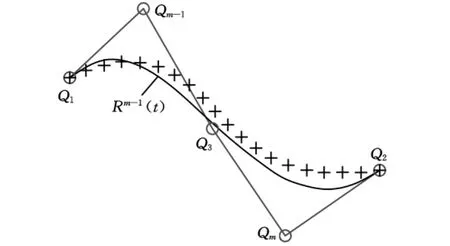
图2 增加控制顶点（m＝5）

（3）迭代调整控制顶点（详见本文第2节）。根据型值点集相对于当前拟合曲线的偏离程度，对所有中间控制顶点Qi（i＝3，4，…，m）的位置进行迭代调整，直到曲线Rm－1（t）达到与｛p j｝的最佳逼近，如图3所示。

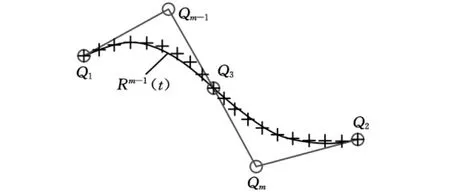
图3 控制顶点调整（m＝5）

（4）拟合收敛判断。如果调整后的Rm－1（t）与｛p j｝的偏离程度满足精度控制要求，则得到最终结果，如图4所示。否则转向步骤2。

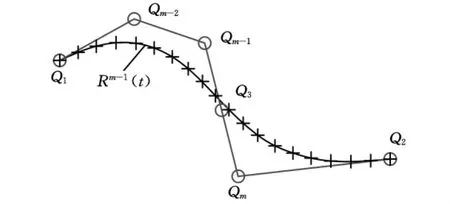
图4 完成交互拟合（m＝6）

2 控制顶点的迭代调整

2.1 参考点组

控制顶点的调整是根据型值点相对于当前特征曲线的偏离程度来计算的。｛p j｝内的某型值点的偏离对各个控制顶点位置调整的影响程度是完全不同的，我们规定每个型值点只作为与其距离最近的控制顶点位置调整的计算依据。

基于这一规定，我们可以为某中间控制顶点Qi（i＝3，4，…，m）分配一组型值点作为其位置调整计算的参考点组｛p j｝（k1≤j≤k2，1≤k1≤k2≤n），如图5所示。

2.2 控制顶点调整的位移计算

某控制顶点Qi的单次调整方向为其在曲线上最近点处的法线方向，调整位移量ξi计算如下：

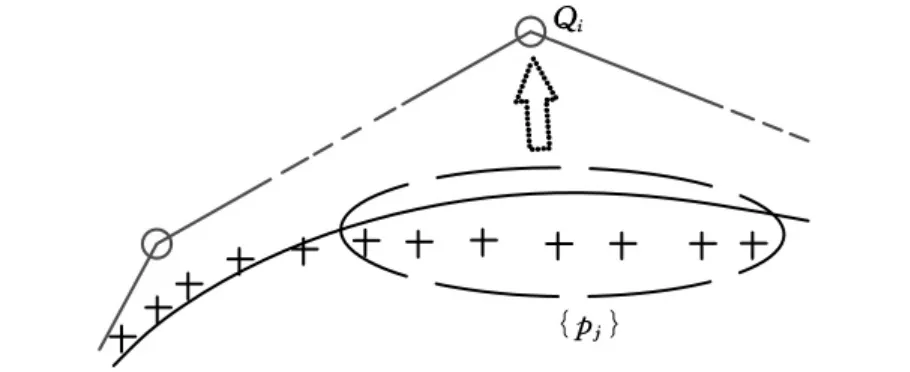
图5 控制顶点调整的参考点组

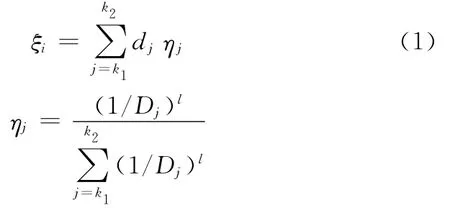
式中，d j为型值点p j到拟合曲线的偏差；ηj为型值点p j对控制顶点位置调整的影响因子；Dj为型值点p j到控制顶点Qi的距离。

其中，l＞1，用于强化距离Dj对ηj的计算结果的影响，l越大，则与Qi距离较近的型值点的影响因子越大，在程序中取l＝2。

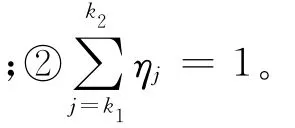
2.3 迭代计算流程

中间控制顶点的位置调整是一个反复迭代过程，其算法基本流程如下：（1）为每个中间控制顶点Qi分配参考点组。（2）按式（1）依次计算并调整各个控制顶点的位置。

（3）计算拟合偏差（最大偏差及平均偏差）的减小（改善）值是否小于规定的阈值，若是，则停止调整；否则返回步骤1继续调整。

2.4 算法的可行性条件

在为控制顶点分配对应的调整点组时，以某型值点到各控制顶点的空间距离为判定标准，将该型值点放入与其最近的控制顶点的参考点组，作为该控制点的调整依据。

但在图6所示的曲线急剧弯曲情况下，这一分组判别将会失效。不仅如此，对控制顶点位置移动矢量方向的计算也会出现错误。所以，我们要求所拟合的目标曲线的曲率变化足够小。幸运的是，在工程实际项目中，曲线一般都比较“平缓”，图6所示的情况极少发生。

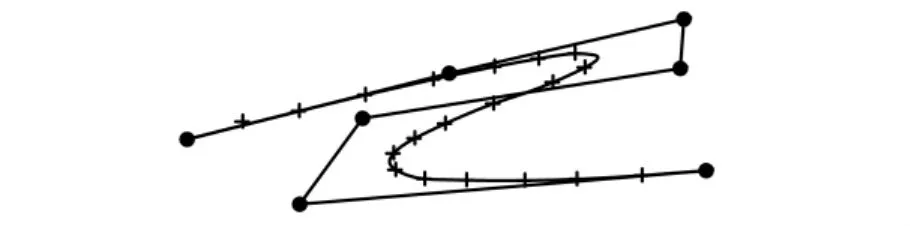
图6 异常的情况

3 应用实例

我们在UG NX软件平台上采用GRIP二次开发工具实现了本文提出的自由曲线交互拟合程序。

本文对图7所示的一组三坐标测量点进行了拟合比对实验，拟合精度设定为0.1mm。图7a所示为采用CAD软件进行拟合得到的5阶自由曲线。由图可见，其最大拟合偏差为0.084mm，同时，拟合曲线的中间两个控制顶点波动较大，曲线两端曲率梳曲线出现了“翘起”的现象。

图7b所示则为采用交互拟合技术得到的5阶拟合曲线，各控制顶点分布均匀，波动小，曲率梳整体变化平缓、一致，同时，其最大拟合偏差仅有0.05mm，相比图7a明显得到改善。

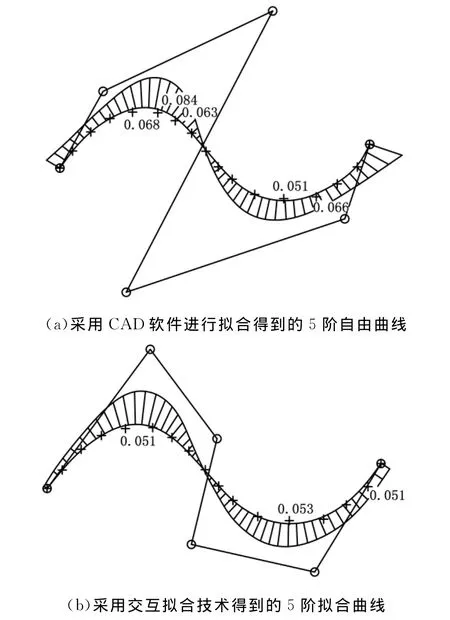
图7 拟合对比实验

采用交互拟合技术生成的边界曲线可用于构造高光顺的曲面。图8为某汽车内饰顶部主体曲面逆向建模的结果，其U、V两个参数方向的曲率均表现出令人满意的结果。

4 结语

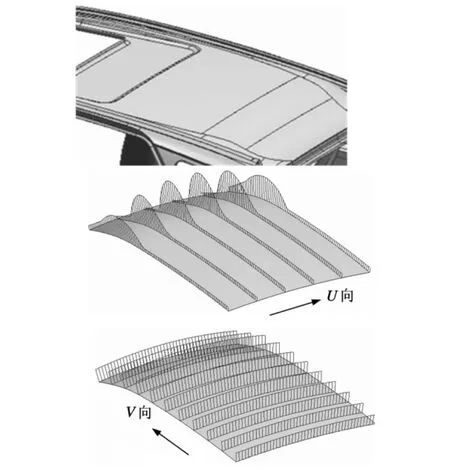
图8 应用实例

本文提出的自由曲线交互式拟合技术较好地解决了现有CAD软件拟合功能无法保证控制顶点分布质量的问题，从而确保了拟合曲线的光顺度。同时，通过全自动调整控制顶点位置，保证了拟合的效率和精度。实际应用效果证明，该方法可较好地满足自由曲线拟合在质量、效率方面的综合要求，有较高的工程实用价值，在汽车零部件逆向设计等领域有广泛的应用前景。

［1］Piegl L，Tiller W.The NURBS Book［M］.New York：Springer，1997.

［2］郭隐彪，郭江，王振忠.非球面检测路径与高精度曲线拟合算法研究［J］.中国机械工程，2008，19（10）：1201－1204.

Guo Yinbiao，Guo Jiang，Wang Zhenzhon.Study on Measuring Path and High－precision Curve Fitting Algorithm for Axisymmetric Aspheric Optics［J］.China Mechanical Engineering，2008，19（10）：1201－1204.

［3］杨旭静，胡仲勋，钟志华.面向刀具路径生成的NURBS曲线拟合算法研究［J］.中国机械工程，2009，20（8）：984－1007.

Yang Xujing，Hu Zhongxun，Zhong Zhihua.Research on the NURBS Curve Fitting for Tool Path Generation［J］.China Mechanical Engineering，2009，20（8）：984－1007.

［4］Foley T A.Scattered Data Interpolation and Approximation with Error Bounds［J］.Computer Aided Geometric Design，1986，3（3）：163－177.

［5］Bajaj C，Xu G.Error Bounded Regular Algebraic Spline Curves［C］//Proceedings of the Fifteenth Annual ACM Symposium on Computational Geometry.Miami Beach，FL.，1999：332－340.

［6］Park H.An Error－bounded Approximate Method for Representing Planar Curves in B－splines［J］.Computer Aided Geometric Design，2004，21（5）：479－497.

［7］Lee E T Y.Choosing Nodes in Parametric Curve Interpolation［J］.Computer Aided Design，1989，21（6）：363－370.

［8］蔺宏伟，王国瑾，董辰世.用迭代B－spline曲线曲面拟合给定点集［J］.中国科学（E 辑），2003，33（10）：912－923.

Ling Hongwei，Wang Guojin，Dong Chenshi.Curve＆ Surface Fitting a Given Point Set Using Iteratively B－spline［J］.Science China E，2003，33（10）：912－923.

［9］刘鼎元，赵玉琦，詹廷雄，等.Bézier曲线和B样条曲线光顺拟合法［J］.计算数学，1984，6（4）：360－365.

Liu Dingyuan，Zhao Yuqi，Zhan Yanxiong，et al.Smooth Fitting Using Bézier Curve and B Spline Curve［J］.Journal of Computational Mathematics，1984，6（4）：360－365.

［10］王国瑾，王振武，寿华好.B样条曲面在严格约束状态下的光顺拟合［J］.软件学报，1998，9（9）：696－698.

Wang Guoqin，Wang Zhenwu，Shou Huahao.Smooth Fitting Using B Spline Curve in Strict Constraint Condition［J］.Journal of Software，1998，9（9）：696－698.