Bézier曲线在五轴直线插补刀路优化中的应用*

刘 江，黄 可，陶永德，丁仁华

(常州机电职业技术学院 机械工程学院，江苏 常州 213164)

0 引言

在数控加工中，所有的数控程序都由最基本的插补指令构成，插补指令可以分为直线插补与圆弧插补[1-2]。圆弧插补过程中，刀具切线方向和圆弧曲率连续性好，带来的速度波动与机械冲击都较小，加工状态较好。但在直线插补过程中，线段曲率与刀具切向会发生突变，导致进给速度会发生波动，容易使机床发生震颤，降低零件表面质量[3]。3轴数控加工中使用的直线插补，可以在去余量过程中，经过CAM软件在直线插补拐角处适当的增加圆角过渡，或使用摆动路径进行加工，已有较为系统的研究成果[4-5]。对于五轴刀路光顺，目前还处在探索的阶段，比较有效的方法有：转接光顺，拟合光顺。拟合光顺算法是对离散小线段采用高阶样条曲线进行逼近，所以计算量比较大，难以控制拟合精度，在实时计算环境中很难使用[6]。转接光顺则用高阶连续的样条曲线或圆弧对小线段拐点处进行过渡[7]。文献[8]对五轴机床数控代码进行了轨迹插补计算，分别用3次Bézier曲线对旋转轴和直线轴进行光顺。

文献[9]对刀轴矢量与刀位点进行了转接光顺，速度规划方法存在一定的迭代过程，需要对多元非线性方程组用雅可比迭代求解算法进行计算。文献[10-11]针对各进给轴的加速度在转接点处不连续，分别对刀轴和刀位点进行转接光顺，使得刀轴满足G2连续，但刀位点没有实现G2连续。5轴数控程序在程序编制时要同时考虑刀轴以及刀位点对零件的影响，刀具光顺计算更加复杂，主要有以下问题：工件坐标系映射到机床坐标系需要经过RTCP转换，各进给轴的运动也同样会受RTCP转换的影响；刀轴与刀位点的误差控制及同步参数化；补偿必须具有实时性[12]。目前，这些问题仍需深入研究。围绕这些问题，本文提出一种新的5轴机床刀路光顺方法，将5轴机床直线插补所采用的球面坐标系，转换成平面笛卡尔坐标系，分别对刀轴矢量和刀位点轨迹进行光顺。平面笛卡尔坐标系中用2个欧拉角表示刀轴矢量，结合基于机床特性的前瞻技术与运动学约束，以满足进给轴速度与加速度光滑连续。

1 5轴直线插补G2连续转接光顺

G2连续转接光顺即直线刀路连接处具有公共的曲率矢。5轴加工过程中刀具路径G2连续可以减小加工过程中的震动，G2连续性的最低阶次曲线为3次曲线，本文为了保证旋转轴与直线轴同时满足G2连续，并且在加工过程中实时同步，采用3次Bézier曲线分别对刀轴与刀位点进行光顺。Bézier曲线的定义如下[12]：

(1)

式中，t是Bézier曲线中的定义参数，0≤t≤1，Bj则对应的是Bézier曲线的各个控制点。

1.1 刀位点的光顺

图1所示为Bézier曲线光顺示意图，P0、P1、P2分别定义线段P0P1和线段P1P2的端点，线段P0P1的单位矢量用T1表示，线段P1P2的单位矢量用T2表示，转接过渡圆弧的4个控制点为：{B0,B1,B2,B3} ，且

d=P1B3=B0P1

(2)

将式(1)进行化简，可以将式(2)代入式(1)得出：

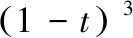
(3)

转接圆弧与原插补路径的最大直线距离，当t=0.5时最大，最大偏差距离为：

(4)

因此，当给定刀尖点的光顺误差ε，转接长度d可以如下计算，当刀位点的转接误差为ε时，光顺圆弧长度d可表示为：

(5)

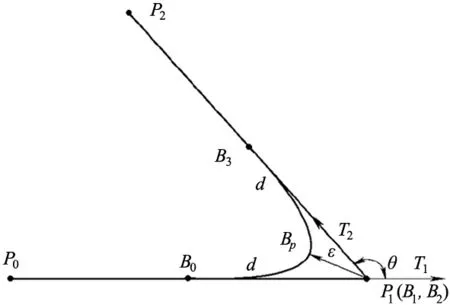
图1 Bézier曲线光顺示意图

1.2 刀轴矢量转接光顺

刀轴矢量的转接光顺与刀位点的光顺有所区别，具体如图2所示，都是采用3次Bézier曲线进行转接光顺，不同的是刀轴方向用o=[oi,oj,ok]表示，为了便于表达，将刀轴矢量通过两个欧拉角度转换成平面矢量，如式(6)：

α=arctan(oj/oi)
β=arccos(ok)

(6)

基于式(6)的映射关系，结合式(3)和式(5)即可确定刀轴的转接光顺曲线，在球面坐标系中刀轴如图2所示，Q=[α,β]表示该平面内与o所对应的点，在确定转接误差εq时，刀轴的方向误差εo与转接误差εq有如下关系：

εq<εo

(7)

图2 球面坐标系转换平面坐标系

图2中,△abc中欧拉角与刀轴矢量关系为：

(8)

可由三角形边长关系得出：

(9)

bc与ab的夹角：

∠abc=arccos(cos(180-β-0.5Δβ)cos(90-0.5Δα))

(10)

由于ε和Δβ、Δα都较小，可以忽略，式(8)可化简为：

(11)

将cos(90-Δα/2)≈0，带入式(10)，可得出：

∠abc≈90

(12)

将式(11)、式(12)带入式(9)得：

ε2=(sinβ)2△α2+△β2

(13)

因为εq<εo，可得：

(14)

刀轴是通过欧拉角转换成平面问题进行转接光顺的，实际应用中需要将平面计算结果重新返回到球面坐标系，Q所对应的球面坐标内，刀轴o=[oi,oj,ok]符合：

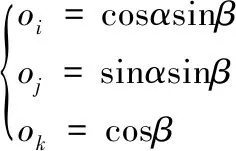
(15)

1.3 刀位点与刀轴光顺同步性

在5轴直线插补中，刀位点转接光顺与刀轴转接光顺的同步性非常重要，即要求同时开始转接光顺，同时结束转接光顺，保证各直线轴和旋转轴速度与加速度没有突变，保持连续。转接光顺后的5轴直线插补轨迹，Bézier曲线圆整了曲线拼接区域，同时满足刀轴与刀位点的转接要求，光顺刀位点与刀轴的曲线采用相同的曲线参数进行圆整，可以实现实时的同步，选择相同的曲线参数时，必须满足以下条件：

(16)

式(16)中各参数如图3所示，BQ(t)在刀路QiQi+1的光顺长度用dq2表示；BP(t)在刀路PiPi+1的光顺长度用dp2表示；BQ(t)在刀路Qi-1Qi的光顺长度用dq1表示；BP(t)在刀路Pi-1Pi的光顺长度用dP1表示。

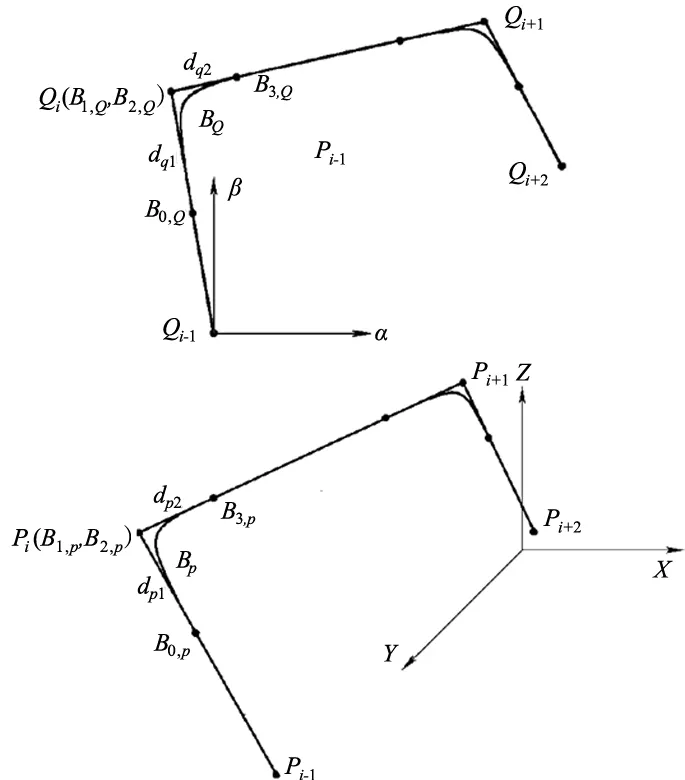
图3 转接同步示意图

2 光顺后直线插补轨迹生成

利用Bézier曲线将5轴直线插补轨迹进行光顺，图4为非对称与对称转接曲线，光顺后的轨迹引进了曲线，曲线的曲率越大，弓高误差越大，向心加速度越大，是制约进给速度的重要因素。文献[11]给出，曲率最大值点的进给速度必须进行限制，当Bézier曲线对称，最大曲率极值在曲线的中点t=0.5处，最大曲率可以表示为：

(17)

图4 非对称与对称转接曲线

速度规划单元可以依据光顺后插补路径的曲率来分，将Bézier曲线的中点定义为分割点，对任意两个分割点之间的路径进行插补计算及速度规划。刀具路径经过光顺，实现高阶几何连续性，位移对时间的导数可以体现运动的平滑性。运动的平滑性越好，所对应的导数连续性越高，所以路径的连续性取决于插补轨迹的几何特性。根据分段函数进行进给轴的加减速控制，更符合伺服电机的机械特性。直线轴与旋转轴的加速度也需要限制。7段式S型速度规划方法如图5所示，可以根据分段函数实时规划出跃度曲线，连续的直线轴与旋转轴加速度曲线，相较于其他速度规划方法，可获得更高的进给速度，规划加速计算时间也可以更长。CNC5轴加工数控系统，在进行5轴直线插补过程中，会执行程序预读功能，例如在直线插补PiPi+1段，PN-1PN之间的路径，已经被预读到系统内部，进行路径规划。所以光顺后直线插补轨迹生成都要经过以下几步。

(1)直线插补轨迹计算，根据生成的速度曲线对加工刀位点与刀轴进行插补计算;

(2)速度规划，根据直线插补的起点和终点通过7段式S型速度规划对跃度、加速度、进给率、路径长度、速度，进行规划，最终得到加速度连续的速度曲线，减小直线轴与旋转轴的机械冲击;

(4)路径光顺，计算出Bézier曲线和线段的表达式就能对PO和PN之间的轨迹进行光顺。窗口末端不需要进行光顺，保证末端执行器加工结束后能够平稳地停在PN。

图5 7段式S型速度规划方法

3 仿真模拟分析与试验验证

3.1 仿真模拟分析

为了对光顺后的5轴直线插补轨迹进行模拟验证，特设计如图6所示的刀路轨迹，在模拟过程中，刀轴的转接误差为0.05°，刀位点的转接误差为0.08mm，最大进给速度F为80mm/s，插补周期Ts设定为0.2ms，最大切向跃度Jmax设置为4000mm/s3，最大切向加速度Amax设置为230mm/s2，具体机床结构如图7所示，各轴运动学模型转换成:

X=Pysin(C)-Pxcos(C)
Y=(Pz+Lac,z)sin(A)-ycos(A)sin(C)-Pxcos(A)sin(C)
Z=(Pz+Lac,z)cos(A)+ycos(C)sin(A)+Pxsin(A)sin(C)
A=arccos(ok)
C=arctan(oi/oj)

(18)

式(18)中，5轴机床的直线轴X，Y，Z最大速度为200mm/s，最大加速度为1000mm/s2，旋转轴A,C的最大速度为10rad/s,最大加速度为30rad/s2，Lac,z为5轴机床内部设置参数，设置为45。结构图见图7。

图6 用于仿真模拟的5轴直线插补刀路

图7 双转台5轴机床结构图

上述仿真模拟计算在数据处理软件Matlab7.0环境下分析计算。为了避免大的计算量同时提高进给率，在程序预读时预读3条直线插补路径，Matlab7.0计算结果如图8～图11所示。

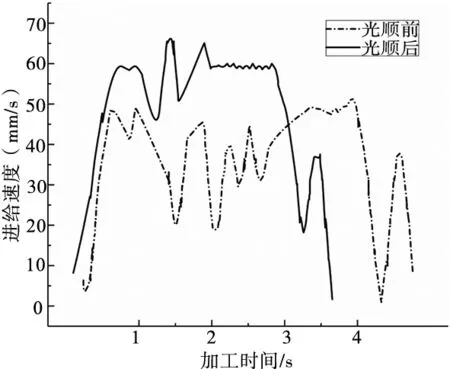
图8 进给速度对比图

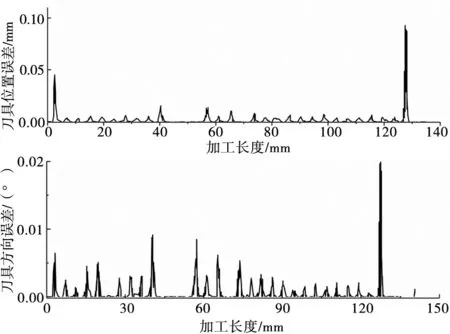
图9 转接光顺误差

在Mori Seiki NMV5000数控系统中模拟加工，各刀位点的距离比较近，且各进给轴进给方向变化比较多，所需加工时间为3.50s，从图8可以看出，光顺后的加工时间为2.93s，光顺前的加工时间为3.82s，综合比较光顺后所需的时间最少。光顺后的5轴直线插补轨迹与原轨迹会产生一定的偏差，偏差的来源为原本突变的离散刀位点被Bézier曲线圆滑过渡，图9中可以看出光顺误差确实存在，刀轴方向的误差范围约为0～0.02°，刀位点的误差范围为0～0.1mm，都没有超过系统的预设值。因此本文采用的Bézier曲线圆滑过渡离散刀位点的过渡方法可以满足误差要求。

图10所示为各轴的进给速度曲线，在仅考虑运动学约束情况下，X轴的速度在进给到18～35mm范围内反向达到最大值；图11所示为各轴的加速度曲线，X轴在加工到40mm和58mm处加速度超出允许最大值，Y轴在加工到40mm处加速度超出允许最大值，C轴在加工到40mm和58mm处加速度超出允许最大值。当同时考虑运动学和伺服约束时，图10和图11中所有的速度与加速度点都处于正负极限之间，验证了Bézier曲线圆滑过渡离散刀位点的合理性。Bézier曲线圆滑过渡离散刀位点的过渡方法中，每个插补点所消耗的直接计算时间为0.186ms，本次模拟共生成839个插补点，因此实时性可以满足。

图10 各轴的进给速度曲线

图11 各轴的加速度曲线

3.2 试验验证

Bézier曲线圆滑过渡离散刀位点的过渡方法，在仿真模拟环境下能够很好的完成预期结果。接下来在5轴龙门式雕铣机上试验验证，图12所示为试验平台组成图，该平台可以拆分为3个部分。

图12 试验平台组成图

(1)5轴龙门式雕铣机，伺服驱动器采用YASKAWA SGDV系列，直线轴选用线轨接触，提高响应灵敏度，旋转轴采用双转台结构，虽然加工范围受限，但制造工艺简单，完全能够满足本次试验。

(2)d SPACE实时控制系统，主要用于采集各伺服轴的光电编码器信号，并从计算机获取实际插补位置指令，进行伺服闭环控制，最后实现模拟量输出等伺服闭环功能。

(3)计算机，配置为 Intel i5 8400处理器，6GB RAM，主要用于Matlab/Simulink仿真试验的搭建。

表1所示为各轴最大跟踪误差试验结果，图13为各轴的跟踪误差。可以看出，Bézier曲线圆滑过渡离散刀位点的过渡方法，能够提高系统位置控制精度。

表1 各轴最大跟踪误差试验结果

图13 各轴的跟踪误差

4 结论

分别对刀位点与刀轴进行了光顺，在刀轴光顺的过程中引进了欧拉角，将刀轴所在的球面坐标系转换成了平面矢量。刀位点与刀轴的光顺曲线采用参数相同的Bézier曲线，进行圆整，保证了各直线轴和旋转轴速度与加速度没有突变，保证了刀位点转接光顺与刀轴转接光顺的同步性。

光顺后的轨迹引进了Bézier曲线，曲线的曲率越大，弓高误差就越大，向心加速度也越大，制约了进给速度。根据分段函数对进给轴的加减速进行控制，符合伺服电机的机械特性。

对光顺后的5轴直线插补轨迹进行模拟和试验验证。在模拟过程中共生成839个插补点，每个插补点所消耗的直接计算时间为0.186ms，能够满足实时性要求。在5轴龙门式雕铣机上进行验证，光顺后的速度和加速度没有超过最大约束值。