Envelope函数与Chebyshev滤波的滚动轴承故障诊断

尹学慧，黄晋英，张占一，侯尧花，郝高岩

(1.中北大学 机械工程学院，太原 030051；2.北京东方振动和噪声技术研究所，北京 100085)

0 引言

滚动轴承是旋转机械中关键的部件，也是故障多发部件，在机械设备运行状态下，滚动轴承更多受到动载、偏载的冲击和转速多变的影响。传统的基于振动测试的滚动轴承故障诊断技术设定的工况通常是定载、转速。然而，不少重要设备使用的滚动轴承往往并非是在定载荷、定转速的工况下，例如风力发电机的增速箱的轴承[1]，直升机的变速箱的轴承，生产制造业负荷调节的生产线上使用的轴承等都是运行在变工况下。传统的滚动轴承故障诊断方法难以对变工况下的滚动轴承故障进行准确的监测和有效的识别。

针对变工况滚动轴承故障诊断，姜战伟等提出一种基于Envelope函数和契比雪夫包络特征提取方法。为解决变速滚动轴承故障诊断中特征提取较难的问题，首先需要对信号进行POVMD分解，最后对平稳信号进行估计重采样[2-3]。杨武成等提出阶次跟踪和Hilbert包络解调在滚动轴承故障诊断，Hilbert不是适合所有信号，有时对包络信号的要求也不完全相同[4]。Borghesanin等提出了一种新的在变工况下滚动轴承故障分析包络方法RS-SES，即先求包络信号再在角度域重采样。该方法对信号的重采样有很高的计算效率和有效性，但对频率重采样需要凑式和更多的经验[5]。康海英等运用了阶比跟踪算法，把时域信号转成角度信号以此研究分析变转速下的旋转机械故障诊断，主要采用了计算阶比跟踪法( Computed Order Tracking，COT)，将对角度信号进行分析，研究变速过程中的旋转机械故障诊断[6-7]。

针对变载荷或变转速等变工况下振动信号非平稳特性的特点，提出了一种基于Envelope函数与包络阶次谱的变工况下滚动轴承故障诊断方法，Envelope函数是用求信号中极值的方法求出极大值和极小值，通过内插(用inter1函数)进而计算出信号的上、下包络曲线[8-9]。并通过与传统的基于Hilbert 变换的包络阶次对比，说明本方法的特点及有效性，最后应用于滚动轴承故障诊断。

1 切比雪夫滤波

切比雪夫滤波器有两种类型：切比雪夫Ⅰ型、和切比雪夫Ⅱ型。切比雪夫滤波器具有波动性，切比雪夫Ⅰ型滤波器在通带中具有等波纹响应，而切比雪夫Ⅱ型滤波器在阻带中有等波纹响应。等波纹特性比单调特性的滤波器具有较低的阶次。因此，对于相同的指标，切比雪夫滤波器比巴特沃斯滤波器的阶数低[10-11]。决定滤波器好坏的一个重要参数即为滤波器的阶数。一般在满足性能指标的基础上，滤波器的阶数应该尽可能小，以提高运算速度的要求[12-13]。

Ⅰ型切比雪夫滤波器最为常见。N阶第一类切比雪夫滤波器的幅度与频率关系可用下列公式表示[14-15]：

(1)

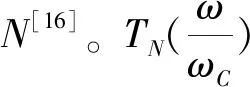
(2)

其递推公式为：

(3)

(4)

(5)

对式(1)两端同时平方，得切比雪夫Ⅰ型低通滤波器幅度平方特性为[17]：

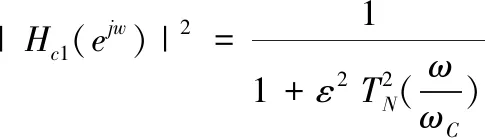
(6)

切比雪夫Ⅱ型低通滤波器的幅度平方特性为：

(7)

根据式(1)和切比雪夫多项式的性质，N阶归一化低通切比雪夫滤波器具有下列基本特征：

(1)当ω=0，N为偶数时，|Hc1(ejw)|2=1-δ1，N为奇数时，|Hc1(ejw)|2=1

(2)当ω=ωc时，无论N为奇数还是偶数，都有|Hc1(ejw)|2=1-δ1，所以ωc为切比雪夫滤波器的通带截止频率。

(4)当ω≥ωc时，|Hc1(ejw)|2会随着ω的增大迅速单调递减到0。

2 仿真信号包络阶次分析

以下用含有直流分量的仿真信号说Envelope函数包络的特性，并与Hilbert变换进行对比。仿真信号为变频调制信号公式如下：

y(t)=t×sin(20πt2×5.2)×cos(2πt×350)+0.5

信号采样频率设置为4096 Hz，高频载波信号为350 Hz，变频信号频率从1s内由0Hz线性递增变到10Hz，模拟变载，变频，含直流分量的仿真信号如图1所示。

图1 原始信号及键相脉冲

对原始信号进行Hilbert变换结果如图2所示。

图2 Hilbert包络

可以看出，通过Hilbert函数求信号得的包络似乎不是信号包络，而是原有的信号，之所以这样不理想的信号包络线是直流分量造成的。

仿真结果分析说明如果信号中有直流分量，需要对信号先消除直流分量或滤波再求出信号的包络线如图3，再在包络线上叠加直流分量恢复原始信号的包络线。然而，实际实验中，由于工作环境和实验条件的原因，很难保证信号中不存在趋势项， Hilbert包络线不一定适用于所有信号，有时对包络线的要求也不完全相同，以下用Envelope函数对模拟信号进行包络，结果如图4所示。

图3 去直流分量的 Hilbert包络

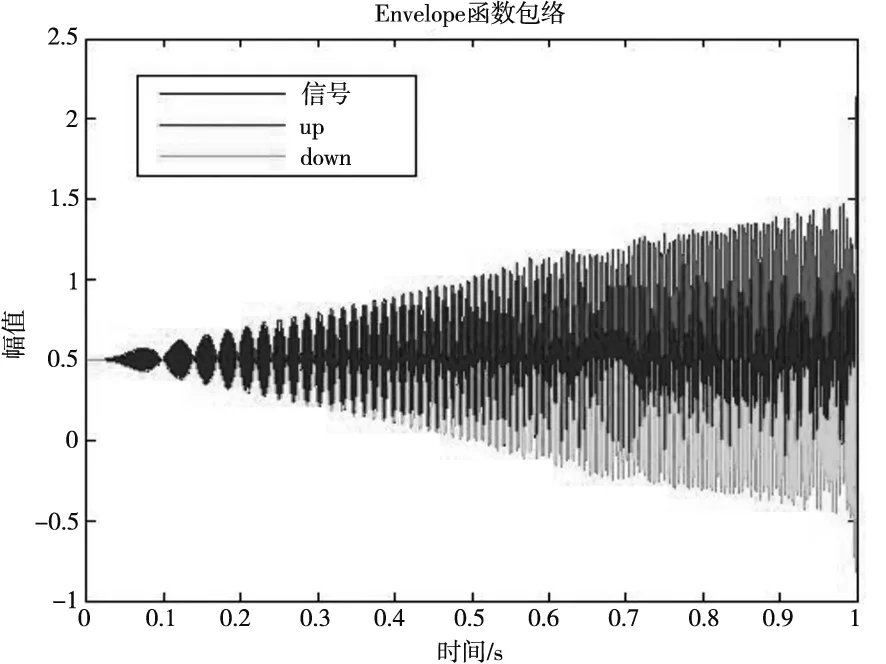
图4 Envelope函数包络

通过对仿真信号两种包络结果对比可以看出，在变工况情况下，未消除趋势项的Hilbert变换包络结果不能将原始信号包络出来，基本就是原始信号；去直流分量的Hilebert包络计算完后，需要对其包络信号加上直流部分，然而从包络的幅值可以看出，Hilbert包络结果并不是很完整，需要对 原始信号进行滤波处理，且也漏掉了信号中的很多重要信息，并不是理想结果；而用Envelope函数包络仿真信号，可以不用消除信号中的直流成分，避免了趋势项的问题，能更准确的得到包络信号的信息。

下面对仿真信号进行Hilbert包络和Envelope函数包络的结果进行阶次分析。

调制信号的Envelope函数包络和Hilbert变换包络的阶次谱如图5和图6所示，仿真信号对应的理论阶次为5.2，两种包络方法在未经滤波和去直流风量处理的情况下，调制阶次5.215均被成功解调出来。消除趋势项的Hilbert变换包络阶次谱如图7所示。从图5和图6两种阶次谱对比可以看出，未消除趋势项的信号，经过Hilbert变换包络后，包络信号基本接近原始信号，导致其阶次谱中阶次成分较多，使得阶次成分有很大的不确定性，影响对轴承故障频率分析，诊断效果较差；而未消除趋势项的Envelop函数包络，其阶次谱中只有单一的阶次成分，便于故障分析。

图5 基于Envelope函数的包络阶次

图6 基于Hilbert变换的信号包络阶次

图7 消除趋势项的Hilbert变换包络阶次

3 变工况下Envelope函数包络的应用

包络阶次主要分为求信号的包括值和角度域重采样两部分，本文选用Envelope函数包络，其包络、阶次流程如图8所示。

图8 流程图

采集仪图9a型号为INV3062-c1(s)，用图9b中9822 ICP型加速度传感器测量轴承振动信号，采用图9c光电速度传感器计算速度脉冲，实验台为图9d的1612多功能转子实验台，轴承故障类型为内圈有裂纹，原始信号为从0～30s加速再减速的过程如图10所示。

(a) 采集仪 (b) 加速度传感器

(c) 光电传感器 (d) 实验台 图9 实验器材

(a) 原始信号波形

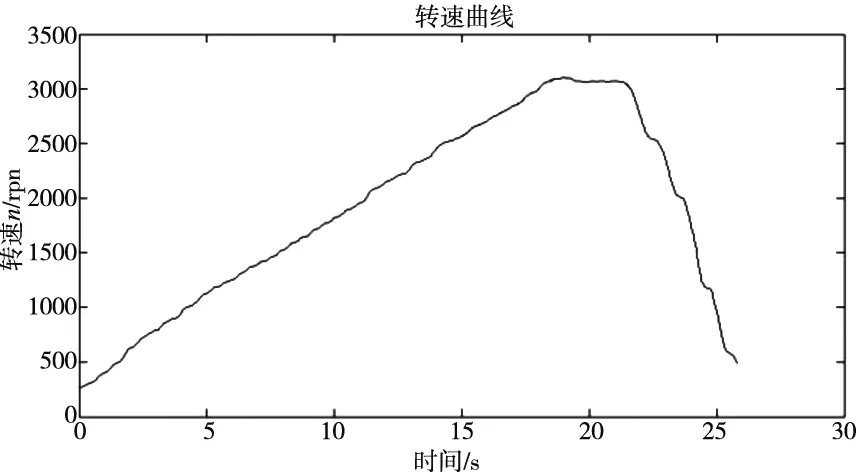
(b) 原始信号转速曲线 图10 原始信号及转速曲线

从原始信号截取5s～10s数据，截断后数据从0s开始 电机转速从640转～1400转，其中，采样频率为20.48kHz，故障轴承型号为6200Z 深沟球轴承，波形如图11所示，根据转速信号可以看出，时域波形的振幅大体上经历了由小变大的过程。

(a) 截断后的振动信号

(b) 截断后的转速信号 图11 截断信号及转速曲线

为验证Envelope函数包络方法的有效性，下面分别，首先内圈故障信号进行包络及乱，为避免角度域重采样频率过小产生阶次混叠，再对包络信号进行低通滤波，滤波方法均采用切比雪夫低通滤波，提高信噪比，并有效抑制了转速变化引起幅值波动，以减小对后续故障阶次分析的影响。

图12 基于Envelope函数包络阶次

图13 基于Hilbert变换的包络阶次

4 结论

针对变工况滚动轴承故障诊断中由速度或载荷波动引起信号的趋势项问题，采用了基于Evelope函数包络和切比雪夫滤波相结合的方法。通过对仿真信号和实验信的两种包络阶次分析方法对比，得到以下结论：

(1)仿真和实验分析表明:在变工况下Envelope函数包络法能够在一定条件下，将低阶变频信号解调出；

(2)切比雪夫低通滤波可明显抑制转速波动引起的振动趋势变化，提高了信噪比，有利于变速工况下的滚动轴承故障诊断；

(3)实验数据分析表明，基于切比雪夫滤波和Envelope函数包络阶次的特征提取方法可以实现滚动轴承故障诊断，是一种有效的变速工况故障诊断方法。