切比雪夫不等式证明的启示及应用

杨 乾

(西南交通大学峨眉校区,四川峨眉山 614202)

切比雪夫不等式证明的启示及应用

杨 乾

(西南交通大学峨眉校区,四川峨眉山 614202)

通过对切比雪夫不等式的证明,得到含数学期望和方差的概率不等式的证法。阐述了切比雪夫不等式是证明切比雪夫大数定律的重要工具和理论基础,在概率论及其实际生活中有很多应用。

切比雪夫不等式;数学期望;方差

一、启示:含有期望和方差的概率不等式的证法

定理:(切比雪夫不等式)设随机变量X具有数学期望E(X)=μ,方差D(X)=σ2,则对任意的正数ε,有

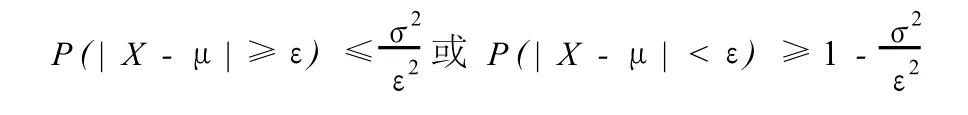
证:设X为连续性随机变量,概率密度为f(x),则

切比雪夫不等式的证明步骤:

1)先将随机变量在区间内取值的概率用其概率密度在该区间上的积分表示;

2)利用随机变量取值满足的不等式,将被积函数扩大,产生概率不等式;

3)将积分区间扩大到(-∞,+∞),将积分再次扩大,切使积分化为随机变量或随机变量的函数的期望或方差的表达式,则得要证的概率不等式。

从中我们得到含期望和方差的概率不等式的证法。

二、切比雪夫不等式的应用

切比雪夫不等式主要有2个方面的应用:

1)利用切比雪夫不等式估计随机变量X落入区间(a,b)内的概率P(aXb),关键是将待估概率P(aXb)化为的形式,方法是将不等式aXb的各端同减去E(X)

解:第一步:求E(X)和D(X)

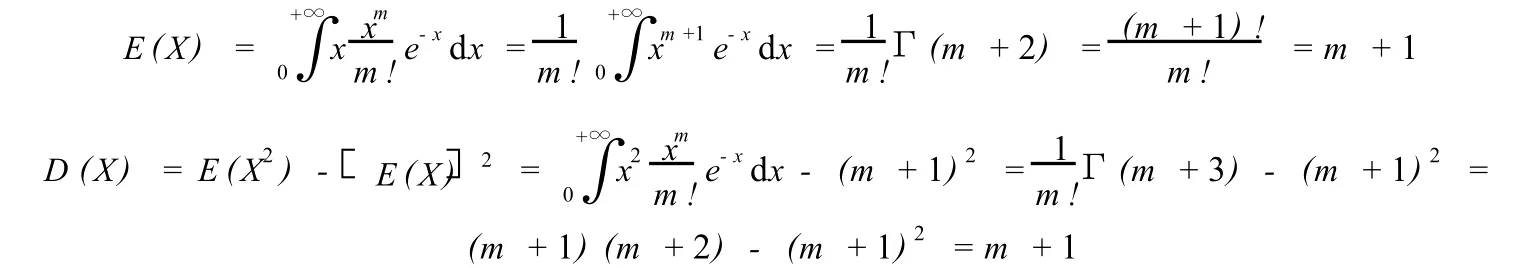
第二步:将不等式0X2(m+1)的各端同减去E(X)=m+1,把待估概率化成P(|X-E(X)|ε)的形式

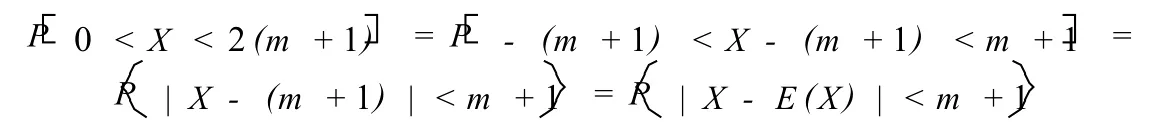
第三步:取ε=m+1,利用切比雪夫不等式估计概率

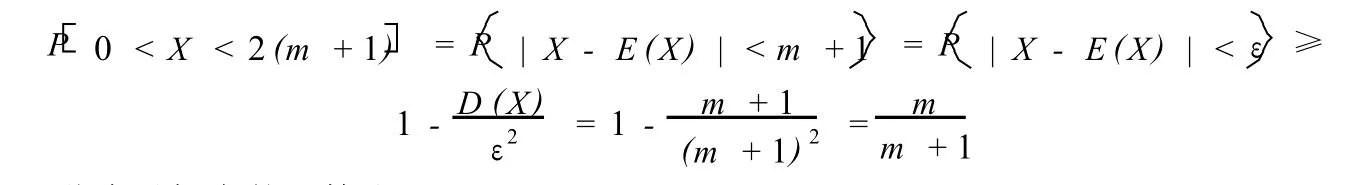
2)求解或证明一些有关概率的不等式

例2 设在每次试验中,事件A发生的概率为0.75,利用切比雪夫不等式求:

n需要多大时,才能使得在n次独立重复试验中,事件A出现的频率在0.74～0.76之间的概率至少为0.90?

解:设X为n次试验中,事件A出现的次数,则X～B(n,0.75)

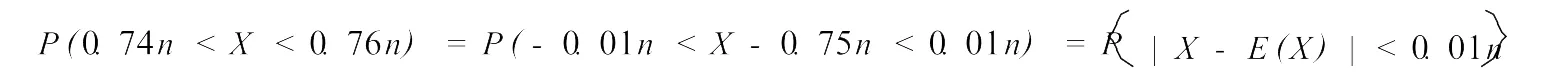
在切比雪夫不等式中取ε=0.01n,则

即n取18750时,可以使得在n次独立重复试验中,事件A出现的频率在0.74～0.76之间的概率至少为0.90

[1]沈恒范.概率论与数理统计教程[M].4版.北京:高等教育出版社,2003.

[2]陈永华.概率论与数理统计[M].杭州:浙江大学出版社,2005.

(责任编辑周江川)

O21

A

1007-7111(2011)01-0119-02

2010-11-28

杨乾(1990—),男,研究方向:概率论与数理统计。