协作机器人关节摩擦特性辨识与补偿技术*
陶 岳,赵 飞,曹巨江
( 1. 陕西科技大学 机电工程学院,西安 710021 ; 2. 西安交通大学 机械工程学院,西安 710049;3. 陕西智能机器人重点实验室,西安 710049)
0 引言
随着机器人技术的不断发展,使用机器人代替人的繁复劳动已成为目前各行业降低成本、提高制造质量的主要手段。应用行业的扩展,对机器人的易用性提出了更高的要求。因摩擦造成的位置精度和运动平稳性降低的现象在机器人启停或低速运动时表现明显。加之机械臂的位移放大作用,机器人关节的摩擦特性与补偿的研究具有重要的意义。
已有众多学者实现了伺服系统的摩擦辨识和补偿的研究。李鹏勃等[1]采用EMD和最小二乘法进行了Stribeck模型的参数辨识;陈光胜等[2]基于泰勒展开将Stribeck摩擦模型转化为摩擦模型的线性化表示,采用最小二乘法进行参数拟合辨识;黄晓勇等[3-4]结合数控机床的进给系统的机电特性,从指令、控制器和摩擦特性的角度综合分析了摩擦误差产生机理并验证了摩擦误差的产生由机电特性共同决定;姚建勇等[5]提出了一种结合了液压马达的摩擦特性的改进LuGre摩擦模型,并进行了参数辨识与前馈补偿,提高了跟踪精度。张从鹏等[6]提出了一种将Stribeck模型与工作台的运动副特性相结合的摩擦模型,并进行了参数辨识与前馈补偿,降低了运动误差。
虽然有学者对机器人运动过程中的摩擦误差进行了分析并实现了补偿[9],但是少有文献从机械系统的结构出发,研究机器人的摩擦特性和补偿技术。本文针对机器人关节的特点,从机电综合特性角度出发,实现了机器人关节的摩擦模型参数辨识及其补偿。首先,本文基于机器人关节结构特性,建立系统动力学模型;其次,建立了sigmoid函数、库伦与黏性相结合的摩擦模型并辨识了模型参数;最后,实现了开展机器人关节摩擦补偿研究。
1 协作机器人关节动力学特性
1.1 模块化可重构关节结构
机器人关节中的重要部件由谐波减速器构成,而谐波减速器中存在多个运动副,这使得机器人关节在转动时受到了较大的摩擦阻力的影响。机器人因摩擦造成的精度和运动稳定性问题主要因素由其造成。本文所使用的机器人关节由SHA伺服执行单元、输出端编码器、扭矩传感器、交叉滚子轴承及针对各元件形状进行适应性设计的连接与支撑零件构成。SHA伺服执行单元本身已经集成了电机、电机端编码器及谐波减速器。SHA伺服执行单元的定子固定在外壳上,输出法兰上固定了一个传动短轴用于安装扭矩传感器和输出端编码器的内圈。交叉滚子轴承外圈固定在外壳上,内圈安装了一个关节输出法兰,输出法兰与扭矩传感器通过花键轴相连接。关节执行单元的转动通过传动短轴、扭矩传感器和花键轴带动输出法兰的转动,进而带动安装于输出法兰上的连杆进行转动。模块化可重构关节结构如图1所示。

1.SHA伺服执行单元 2.传动轴 3.外壳 4.编码器 5.外壳 6.轴承 7.输出法兰 8.花键轴 9.扭矩传感器
图1 模块化可重构关节三维设计图
1.2 动力学建模
机器人的动力学模型是机器人运动控制的基础,描述了关节执行器力矩、摩擦等扰动力和结构运动之间的动态关联关系。对于6自由度机器人来说,其运动学非常复杂,多种因素耦合在一起,为便于研究机器人关节的非线性摩擦对机器人运动的影响,论文使用二自由度机器人进行研究,所设计的机器人系统的受力分析如图2所示。
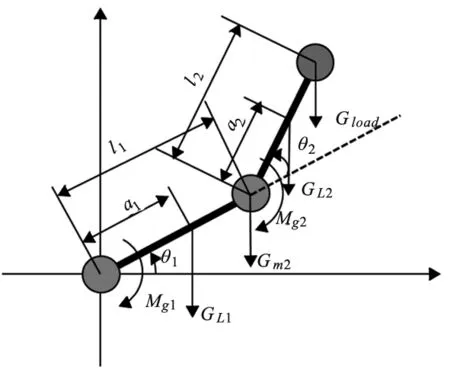
图2 平面二连杆机器人
关节型机器人关节空间动力学模型的简洁矩阵形式如式(1)所示。
(1)
其中,B(q)为惯性矩阵;D为粘滞摩擦系数矩阵;Nμ为库伦擦力矩向量;g(q)为重力矩向量;τ为关节扭矩向量;τe为外力矩向量。
对于本机器人系统其惯性矩阵:
式中,Ili为连杆i转动惯量;kri为关节i的减速比;Imi为关节i的转动惯量。
机器人的系统的固有参数如表1所示。

表1 机器人系统固有参数
2 机器人关节摩擦辨识
2.1 机器人关节摩擦特性分析与建模
库伦+黏性摩擦模型能够有效的反映摩擦特性且结构简单,被广泛应用到伺服系统中反映摩擦特性。该模型考虑了机械系统的阻尼,并通过粘滞摩擦力项来描述阻尼对摩擦力的影响。库伦+黏性摩擦模型如式(2)所示:
f=fcsgn(v)+σv
(2)
式中,fc为库伦摩擦力;σ为粘滞系数。
库伦+粘滞摩擦模型在过零点处不平滑,在摩擦补偿后极易造成机器人换向过程中的抖动现象。本文采用在库伦+黏性摩擦模型中引入了sigmoid函数的方法来平滑模型,sigmoid函数如式(3)所示:
(3)
式中,γ为平滑因子,用于控制模型的平滑程度。
sigmoid函数在模型中不具有量纲,在零点附近函数值由-1平滑过渡到1。过渡的平滑程度由平滑因子γ确定,平滑因子γ对模型平滑性的影响如图3所示。γ越小,则过渡越平滑。本文根据模型的平滑性需求和精度需求选择γ值为140。
改进的粘滞+库伦摩擦模型如式(4)所示:
f=fc·f(v)+σv
(4)
2.2 关节摩擦参数辨识
机器人关节摩擦力矩是被动力矩,无法采用传感器进行直接测量。对于未加负载的关节且保持恒速转动,电机的驱动力矩与外力矩达到平衡,可认为此时的驱动力矩近似等于摩擦力矩。控制电机恒速运转在特定的速度下,测得不同速度下的驱动力矩即为该速度对应的摩擦力矩。拟合各个离散的速度-摩擦力离散点即可获得较为精确的摩擦模型参数。

图3 平滑因子γ对模型平滑性的影响
摩擦模型辨识实验需要确定待测速度点取值间隔。在低速下摩擦力因存在stribeck效应而对于速度的变化敏感。因此,选择采样点时在低速区间内速度观测点间隔较密集。高速区间内摩擦力与速度成近似线性关系,因此,取值较稀疏。本实验中,在0~5 r/min速度区间内等距间隔0.5 r/min共采集10个速度测点,在5~10 r/min的速度区间内等距间隔取2.5 r/min,共采集5个速度测点,总共采集30组数据。
采用最小二乘法对所得到的速度与摩擦力矩进行拟合,辨识所得的各关节摩擦参数如表2所示,拟合结果如图4所示。辨识结果表明,辨识的摩擦模型能够较好的与实验结果吻合。
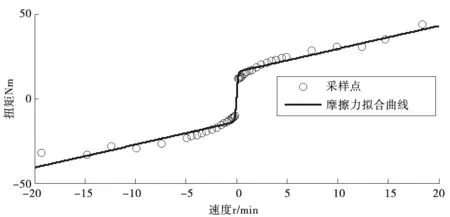
(a) 关节1拟合结果
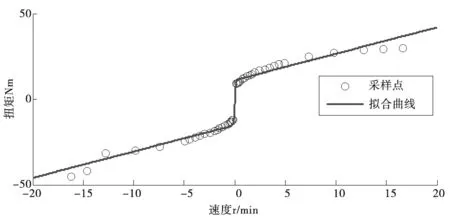
(b) 关节2拟合结果图4 关节摩擦力矩-速度关系拟合结果

参数fcσγ关节113.1401.540140关节214.6301.361140
3 关节摩擦补偿策略
机器人的控制方案上可以分为关节空间控制方案和操作空间集中控制方案两种。关节空间控制方案中,参考输入直接以关节角度的形式输入,由关节直接跟踪输出。这种方案的缺点在于操作空间的运动通过机器人的机械结构以开环的形式进行控制。结构上的任何不确定性都会导致操作空间上的控制精度降低。操作空间集中控制采用整体的方案,将运动学逆解嵌入到反馈回路中。为了提高机器人系统的运动控制精度和稳定性,本文采用操作空间逆动力学控制方法,并在逆动力学控制算法的基础上使用所提出的摩擦模型对关节摩擦进行力矩前馈补偿。
在式(1)中令:
(5)
可以简化机器人动力学方程,可得机器人的控制模型:

(6)
式中,u为控制向量。
选择逆动力学线性控制:
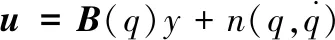
(7)
使得系统表示为双积分器形式:

(8)
由机器人学知识可知,机器人系统的微分运动学方程:
(9)
式中,x为末端执行器位姿;JA(q) 为分析雅克比矩阵。
在JA非奇异方阵的前提下,由式(9)可得:
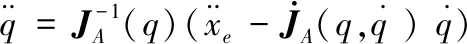
(10)
定义操作空间的姿态误差,
(11)
为使误差渐进稳定并趋近于零,构造如下的线性误差系统:
(12)
式中,KD为误差增益,正定矩阵,决定误差收敛于零的速度;Kp为误差增益,正定矩阵,决定误差收敛于零的速度。
将式(12)代入式(11)、式(10)可获得关节加速度项:
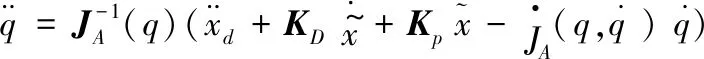
(13)
由此选取逆动力学的控制律如式(14)所示,控制框图如图5所示。
(14)

图5 摩擦补偿控制框图
4 协作机器人摩擦补偿实验
为验证本文提出的改进型库伦+黏性摩擦模型的补偿效果,本文在二自由度机器人实验台上进行实验验证。该实验台由机器人本体和运动控制器组成,如图6所示。机器人本体由自行设计的两个模块化可重构关节、两个关节间的连杆和底座构成,底座上设计了两个安装孔,可分别用于机器人的水平与垂直安装。运动控制器包含基于dSPACE的下位机和基于工控机的上位机构成。下位机进行实时控制和数据采集,上位机进行状态检测和运动指令生成。为排除其他外界干扰并提高系统的控制带宽,本文经过调参后选择KD= diag(1500,1500)和Kp=diag(25,25)。位置指令采用正弦信号x=sin232dt。如图7a所示。

图6 协作机器人系统
为了观察摩擦项参数对关节摩擦的补偿效果,使用前文中提出的摩擦模型对机器人进行摩擦补偿实验。正弦信号具有速度连续变化的特点可以较好地体现系统的性能,因此使用正弦信号观察机器人的摩擦补偿效果。实验结果如图7b所示。
实验结果表明,摩擦补偿明显改善了爬行现象,基本消除了速度“死区”, 使速度在零点附近的过渡变得更加平滑,换向过程中的速度误差峰值从0.002 rad降低到0.0015 rad,改善了机器人换向过程中的抖动,这对于提高机器人系统的运动控制精度和稳定性具有重要的意义。
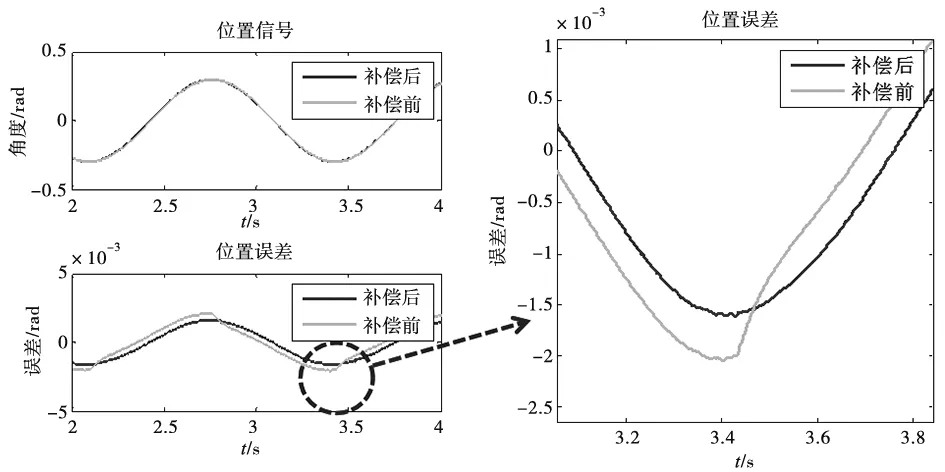
(a) 摩擦补偿前后位置跟踪情况
5 结论
摩擦作为机械系统固有特性,它降低了机器人关节在换向过程和速度运行时的运动精度和平稳性,基于摩擦模型的前馈补偿是重要的改善方法。本文提出的基于sigmoid函数的改进库伦+黏性摩擦模型能够有效的改善机器人关节在低速下的爬行现象,改善了运动的平稳性;同时,降低了换向过程中的速度误差峰值,提升了位置精度。该方法操作简单,实用性强,论文研究对于提高机器人系统的运动控制精度和稳定性具有重要的意义。

