基于改进变异粒子群算法的TDOA/AOA定位研究*
胡 骏,乐英高,b,c,蔡绍堂,曹 莉,吴 浩
(四川理工学院 a.自动化与信息工程学院;b.人工智能四川省重点实验室;c.材料腐蚀与防护四川省重点实验室,四川 自贡 643000)
0 引言
移动通信定位技术[1]是基于美国的全球卫星定位系统GPS(Global Positioning System)、中国的北斗双星BDS(BeiDou Navigation Satellite System)、欧洲的全球卫星导航系统伽利略(Galileo)、全球移动通信系统GSM(Global System for Mobile communication)等卫星定位系统,通过接收基站和移动台之间的无线电波,检测无线电波信号的特征参数,如幅度、信号入射角、传输时间差等,如图1所示。利用参数根据相应的定位算法计算得到移动台的估计几何位置。

图1 移动通信定位
移动通信中研究的无线定位技术[2]有两种实现方案。基于方向的定位技术,如到达角(AOA,Angle of Arrival)定位技术,即利用基站接收机的天线阵列来测量由移动台所发出电波的入射角,并构成移动台到基站的径向连线,多条连线的交点就是移动台的位置;基于距离的定位技术,如到达时间差(TDOA,Time Difference of Arrival)定位技术,即利用基站检测到信号的时间与移动台发射信号的时间差,计算出基站与移动台之间的距离,时间差测量值表现形式为双曲线,多条双曲线的交点就是移动台的位置[3]。现有的AOA定位技术会因为移动台到基站的位置远近,非视距传播以及其他环境改变,使得定位精度大幅降低,如当两者距离较远时,测量角度出现一点的微小偏差,则定位距离会受到很大的影响。而TDOA定位技术对所有参与定位的基站的时间虽然相比于到达时间(TOA,Time of Arrival)没有要求严格的完全同步,但依然对时间基准的依赖性较高[4]。
针对上述的AOA或TDOA所存在的问题,研究人员提出了TDOA/AOA混合定位算法[5]。TDOA/AOA混合定位算法可以充分利用蜂窝网络产生的对移动台位置估计定位的优良电波特征测量值,克服由时间同步和多径传播产生的部分误差,减小环境对定位精度的影响。单一定位技术具有其局限性,因此混合算法结合不同定位算法的优点,必定具有更加精确的定位性能。但TDOA是通过电波到达时间差对移动台(MS,Mobile Station)的位置建立方程,AOA是通过信号到达角度对MS的位置建立方程,如何求解这两种不同类型非线性方程联立的非线性方程组,是各类TDOA/AOA混合定位方法的重点和难点。
1 相关工作
基于TDOA/AOA混合定位算法在对移动台位置估计定位中具有更精确的定位性能,研究者加入了其他算法,来进一步改良TDOA/AOA混合算法[6-8]。现有国内外学者们进行了深入的研究,首先针对减少其受测量误差的影响,例如文献[7]提出一种基于TDOA/AOA混合算法噪声项新的权重最小二乘(WLS,Weighted Least Squares)方法,开发结构化全局最小二乘(STLS)方法;文献[8]提出构建混合测量算法未知源位置之间的新关系,获得的解的均方误差矩阵可以获得小误差区域内的CRB(Cramér-Rao bound)界限。其次对于混合定位中非线性方程组的问题,求解一般有两种基本的方法:一是直接求解非线性方程组得到估计值,文献[9]提出了运用类正态分布密度曲线建立TDOA误差模型,使TDOA误差模型更加接近真实误差,用卡尔曼滤波器对TOA测量值滤波使得TOA更加接近真实的到达时间,是一种实时、直接消除误差的方法;二是通过引入与待求变量有关的附加变量,把待求的非线性方程组转化为伪线性方程组,进而求解,文献[10]介绍的对最小二乘法进行改进,分离出引入的附加变量,使得方程两边分别是MS的坐标和附加变量,最大的优点是能够避免对奇异矩阵求逆。
随着智能优化算法的深入发展,学者们也将智能算法应用到TDOA/AOA混合定位算法中,处理其存在的问题。文献[11]中提到了将遗传算法(GA)运用到TDOA/AOA定位系统中,以混合算法产生的定位误差的CRLB为基准,通过研究改进GA的适应度函数选择和位置编码,提高定位精度,达到寻找最佳的布站策略。文献[12]中将模拟退火遗传算法运用到TDOA/AOA定位中,克服了运用最小二乘法时存在的问题,提高了定位精度和稳定性。文献[13]中将粒子群算法与Chan算法结合,进行协同定位。移动台位置的初始解由粒子群算法估算出,基于初始解来构建残差方程,筛选基站后结合Chan算法对移动台二次定位得到最终的估计位置。
本文借鉴文献[13]提出的粒子群算法对移动台位置初始解预先进行估计的思想,提出将遗传算法中的变异操作加入到粒子群算法的迭代过程中,再将改进的变异粒子群(IMPSO)算法应用到TDOA/AOA混合定位中,使粒子群算法能够快速收敛,达到寻优的目的[14]。该算法首先用最大似然法得到移动台的最大似然估计函数,并将最大似然估计函数作为适应度函数,然后对PSO算法中的适应度方程进行变异操作,同时对惯性权重进行改进,达到PSO算法在对适应度函数进行寻优处理时不会出现陷入局部最优的目的,使获得的移动台的目标坐标更加精准。仿真和对比结果也表明提出改进后的PSO算法具有更优越的定位性能。
2 TDOA/AOA混合定位算法
TDOA/AOA混合定位算法就是综合利用各种信号信息和特征测量值,估计MS的位置的算法,相对于单独的TDOA定位算法或AOA定位算法,将两种算法模型进行结合使用,可以明显提高定位精度,减少测量误差带来的影响。
建立TDOA/AOA混合定位的三维直角坐标系,为了简化计算,基站坐标为(xi,yi,zi),移动台MS坐标(x,y,z),如图2所示。本文研究基站和移动台在二维平面内。
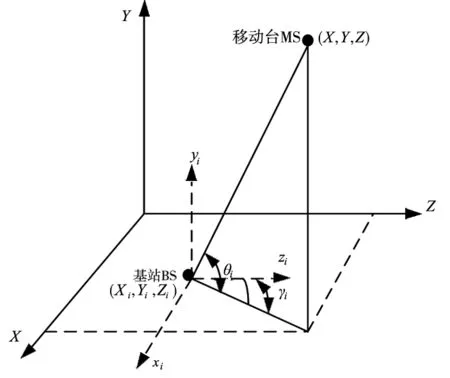
图2 TDOA/AOA联合定位系统模型
假设在二维平面布置了基站接收机M个,第i个基站BS的坐标为(xi,yi),移动台MS的坐标为(x,y),移动台到基站的距离为ri,则根据(TOA)测量值可列出距离方程:
(1)
式中,c为电波传播速度,τi为时间差。
一般选择参考基站为第一个基站,根据TOA的测量值,可得到TDOA的测量值。假设距离差为ri,1,表示移动台到基站i(i≠1)与到基站1的距离差,即:

(2)
式(2)中所示,i=2,3,..M,ni,1是测量TDOA时引入的噪声,ni,1=ni-n1,ni是系统的测量误差,r1是基站1到移动台MS的距离。当信噪比高的时候,可认为TDOA的测量值近似服从正态分布,因此ni,1也可认为近似服从正态分布,假设其均值为0,方差为σ2,假定服务基站BS总能提供MS的AOA测量值,根据AOA测量值α可建立方程:
(3)
式(3)中所示,nα是AOA的测量误差,假设其服从均值为0,方差为α2的正态分布。设Δr=[r2,1,r3,1,…rM,1]T,r=[r2,r3,…rM]T,r1=[r1,r1,…r1]T,n=[n2,1,n3,1,…nM,1]T,据上式可得:
Δr=r-r1+n
(4)
本文采用最大似然法来确定移动台MS的坐标,因为ri,1服从均值为(ri-r1),方差为σ2的正态分布,α服从均值为arctan((y-y1)/(x-x1)),方差为α2的正态分布,假设各测量值相互独立,则移动台位置的最大似然估计为:

(5)
用一般方法求解非线性方程(5),很难得到理想的结果,因此用IMPSO算法优化处理后获得坐标的最优解。
3 基于改进变异粒子群算法
3.1 粒子群优化算法
粒子群算法作为进化算法中的一种,优点是处理优化问题十分有效并且被广泛使用[15]。算法对于所优化的目标函数不存在依赖的关系,同时具有参数少、实现简单等特点,因此广泛应用于解决非线性优化问题。其基本思想为将一组系统已初始化的随机粒子,每个粒子,都是表示目标函数存在的可能解,通过计算分析某种迭代方式进行寻优,得到最优解,即最优解表示移动台MS估计的位置。PSO算法的实现:
设种群中粒子的数量为S,在d维空间中,U=(uk1,uk2,…ukd)和Y=(yk1,yk2,…ykd)分别表示第k个粒子速度与位置,式中k=1,2,…,S,p=1,2,…,d,即p是维度,ykp∈[Lp,Hp],Lp和Hp分别代表空间维度的下界与上界,uSd∈[Umin,d,Umax,d],Umin,d和Umax,d表示粒子的速度,用Qk=(qk1,qk2,…,qkd)表示第k个粒子的最优解,用Qg=(qg1,qg2,…qgd)表示所有种群中的全局最优解,依据公式(6)、式(7)更新每个粒子的速度向量和位置向量。
ukp(z+1)=ωukp(z)+c1r1(qkp(z)-ykp(z))+
c2r2(qgp(z)-ykp(z))
(6)
ykp(z+1)=ykp(z)+ukp(z+1)p=1,2…d
(7)
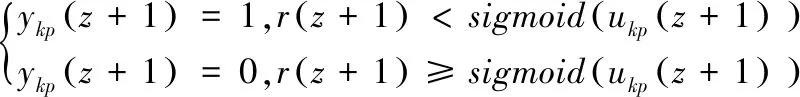
(8)
式(6)中所示,c1和c2分别为加速因子;当前迭代次数为z,最大迭代次数为T;r1和r2取[0,1]之间的随机数;r(z+1)是第z次迭代时在[0,1]之间生成的实数,其中sigmoid函数为:
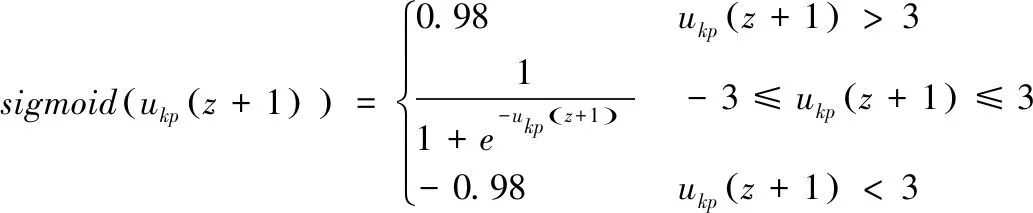
(9)
ω为惯性权重,取值为:
(10)
式(10)中随着粒子的迭代进化,ω∈(ωmin,ωmax)逐渐由大变小。
3.2 适应度函数
适应度函数是改进变异粒子群算法指导搜索方向的依据,在算法中,适应度最佳对应的坐标(x,y)即为移动台坐标。取适应度函数为:

(11)
其值越小代表粒子对函数的适应性越好,则粒子k的个体最优位置由式(12)确定:
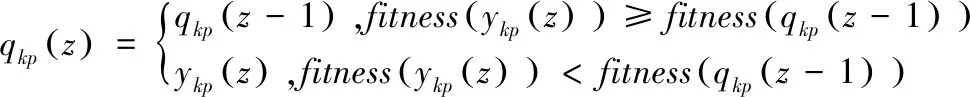
(12)
粒子k的全局最优位置由式(13)确定:
qgk(z)∈{qg1(z),…,qgs(z)|fitness(qgs(z)) =
min{fitness(qg1(z)),…|fitness(qgs(z))}}
(13)
设粒子的坐标矢量定义为:
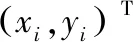
(14)
式(14)中所示,(xi,yi)为移动台待估计的坐标点。设移动台的坐标为(x,y)是在基站所构成的范围内,即:
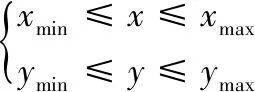
(15)
式(15)中所示,xmin和xmax为基站构成的范围内横坐标的最小值和最大值,ymin和ymax是基站构成的范围内纵坐标的最小值和最大值。
3.3 改进变异粒子群优化算法
传统的PSO算法在求解复杂的多峰值的非线性优化问题中,会出现容易陷入早熟收敛、陷入局部最优等问题[16]。为了解决上述问题,本文结合惯性权重和遗传算法中的变异操作对PSO算法进行改进。
(1)一般而言,惯性权重ω对粒子群算法的性能影响较大。当惯性权重较大时,有利于全局搜索,当惯性权重较小时,能够加速算法收敛,有利于局部搜索。因此,在PSO算法中可以通过改变惯性权重来提升算法的性能。在混合定位中,因为需要分析的数学模型是一个非线性方程组,因此根据式(10)提出一个改进的惯性权重值,进而优化粒子群算法的全局和局部搜索能力:
(16)
式(16)中所示,ω为惯性权重,ωmax为最大惯性因子,ωmin为最小惯性权重,z为当代迭代次数,T为最大迭代次数。
(2)基于粒子位置和速度的更新以及控制种群多样性的基础上,引入变异操作。在算法出现陷入局部聚集的问题时,变异能够让各个粒子重新搜索新的方向。变异操作的执行节点,需根据群体适应度方差值[17]的指标为:

(17)
式(17)中所示,φS为全局最优值的变异概率,ε2为适应度方差,φmax表示变异概率上限,φmax表示变异概率下限。改进后的算法中,当粒子的位置呈现出局部聚集的不足时,算法会对粒子进行变异操作,能够将聚集的粒子重新打散,进行新的方向的搜索。
改进变异粒子群优化算法实现步骤,如图3所示。
①初始化粒子群算法各参数:确定种群规模S,最大迭代次数T,加速因子c1和c2,最大惯性权重ωmax和最小惯性权重ωmin。
②依据式(6)、式(7)更新每个粒子的速度向量和位置向量。保证在[vmin,D,vmax,D]速度区间内,若超出上下限,则分别换为vmin,D和vmax,D;
③根据适应度函数式(11)评价每个粒子的适应度值,将个体最优粒子和全局最优粒子存在Qk和Qg中;
④根据式(16)计算惯性权重ω;
⑤更新粒子的速度和位移,更新粒子的个体最优值和全局最优值;
⑥计算适应度方差ε2以及变异概率φS并产生一个随机数e,如果e<φS则按式(18)变异:
qdg=qgd(1+0.3ξ)
(18)
式(18)中,设ξ服从(0,1)的高斯分布,qgd就是移动台位置;
⑦判断算法是否收敛,满足则继续执行;不满足转第②步;
⑧当迭代次数达到T,则停止迭代,输出最优解。
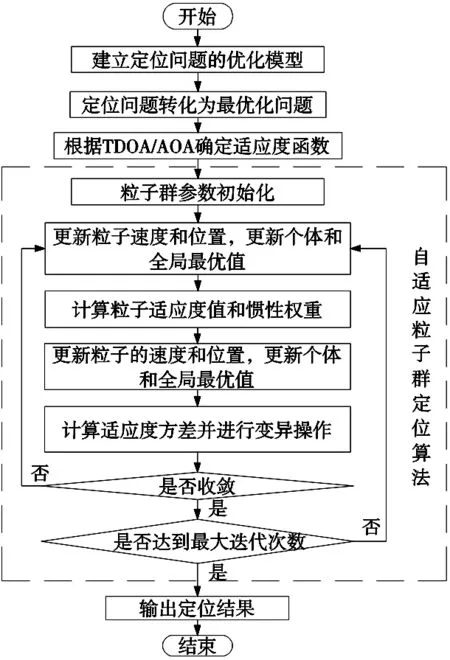
图3 改进变异粒子群优化定位算法流程图
4 计算机仿真及结果分析
本文的实验环境基于MATLAB2014a平台,Windows7,64位系统的计算机。文中,为了体现提出的IMPSO算法的定位性能(均方根误差RMSE和均方误差MSE),仿真结果与传统的Chan算法[18]以及基于最小二乘的TDOA/AOA混合算法[19]进行了比较。


图4 基站与移动台位置示意图
(1)在视距环境下,三种参数对均方根误差(RMSE)的影响。
均方根误差根据式(19)所示:
(19)
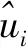
①基站个数对定位性能的影响,由图5可看出,在误差取30m,半径取3000m,随着基站个数由4个到9个的增加。各个算法的定位性能随着基站的增加出现不同的变化情况,如图5所示。
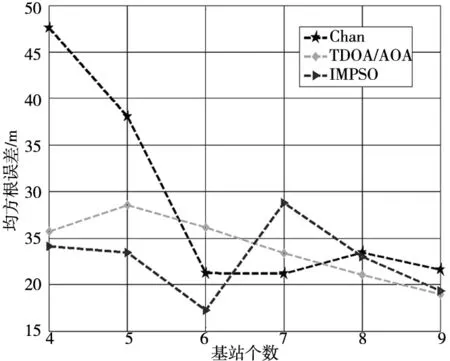
图5 标准误差与基站关系
图5中,当基站个数在4~6个时,IMPSO算法的曲线明显低于另外两种算法,定位性能最佳,混合算法次之;在7~9个基站时,定位性能的差距不大,总体平均值,IMPSO算法相对于Chan算法、TDOA/AOA算法,定位的精度和准确度有明显的提升;图中的粒子群算法曲线的平稳性体现出了算法具有更好的稳定性。
②半径对定位性能的影响,由图6可看出,在基站取7个,测量误差为30m的情况下,随着半径的不断增加,定位误差呈现上升趋势。
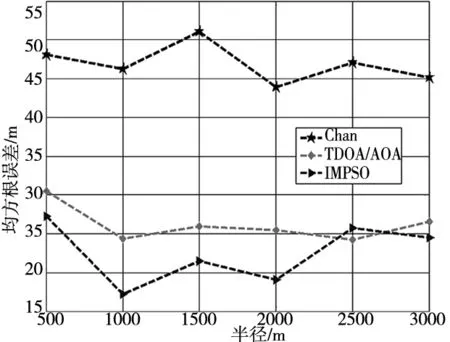
图6 标准误差与半径关系
图6中可以看出,IMPSO算法的定位性能和可靠性相对于其他两种定位算法,具有明显的优越性,这是由于IMPSO算法是对TDOA/AOA的函数式进行寻优,消除了一定的误差,一定程度上减小了由半径变化带来的误差,提高了定位的精度。
③测量误差对定位性能的影响,由图7可以看出,在半径取3000m,基站取7个的情况下,测量误差方差在30m~240m,测量误差x=σAOA×c,c为光速,随着测量误差的增加,其他两种算法的标准误差也随之增加。

图7 标准误差与测量误差关系
图7中,IMPSO算法相对于其他两种算法,在误差小于120 m之前基本不受误差的影响,这是由于IMPSO算法能够有效的抑制误差对定位精度的影响,使得定位性能得到明显的提升。其他两种方法,受误差影响较大,由于随着测量误差的增加,最终的测量结果出现偏差的概率也就越大,算法表现出来的性能也就越不稳定。
(2)在视距环境下,三种参数对均方误差(MSE)的影响
均方误差根据式(20)所示:
(20)
式(20)中所示,x(l)式x的第l次的估计位置值。
①基站个数与均方误差的关系,如图8所示。
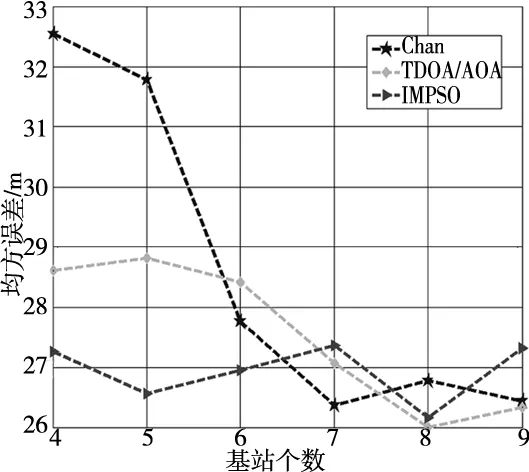
图8 基站与均方误差关系
如图8所示,基站在6个之前,本文提出的IMPSO算法的定位精度明显高于其他两种算法,在基站数大于6个数之后,精度受基站数量的影响不大,原因是修正了BS与MS之间的TDOA测量值,此时是AOA的测量偏差对定位性能起作用。
②半径与均方误差的关系,如图9所示。

图9 半径与均方误差关系
如图9所示,本文提出的IMPSO算法定位性能优于其他两种算法,这是由于粒子群算法中经过变异操作和改进惯性权重后,避免了非线性在运算过程中线性化,继而导致算法陷入局部最优解的问题,使得TDOA/AOA混合定位的定位性能得到了提高,所以将IMPSO算法用于TDOA/AOA混合定位中,能够克服非线性问题,有效提高定位精度。
③测量误差与均方误差的关系,如图10所示。
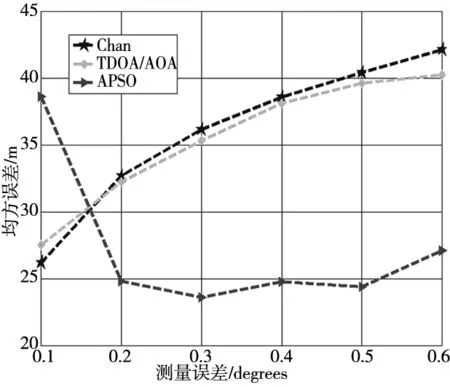
图10 测量误差与均方误差关系
如图10所示,随着测量误差的增加,均方误差也随之递增,IMPSO算法在平均均方误差中,表现出了良好的定位性能,这是由于IMPSO算法降低了测量误差对定位的影响,使得定位更加精确。
(3)三种算法的三维对比关系,如图11所示。
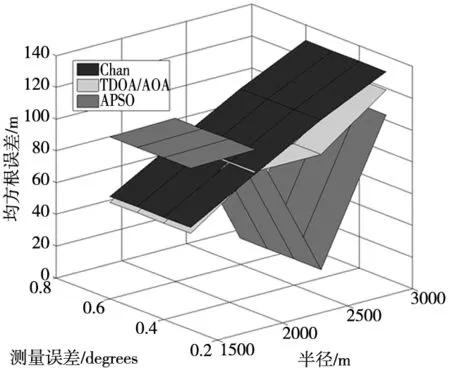
图11 三维对比图
如图11中所示,当半径超过1500m时,本文提出的IMPSO算法比另外两种算法取得更好的定位性能,定位精度得到了明显的提升。
5 结论
文中对IMPSO应用于TDOA/AOA混合定位算法中做了研究,通过运用IMPSO算法,将TDOA/AOA混合定位的函数作为适应度函数进行寻优,找到最佳适应度对应的坐标点,有效的解决了TDOA/AOA混合定位中受误差影响较大,以及非线性优化的问题。从分析和仿真结果可以看出,相对于传统的Chan算法以及TDOA/AOA混合算法,在不同的小区半径和测量误差的情况下,表现出更高的定位精度和可靠性,具有速度快,性能稳定的优点。因此,利用IMPSO对TDOA/AOA混合定位算法进行改进,对目标进行定位,能够有效地获得目标的位置。同时,用IMPSO算法解决其他定位问题也具有一定的研究价值。

