一种基于改进适应度的多机器人协作策略
曾庆山, 冯珊珊
(郑州大学 电气工程学院,河南 郑州 450001)
0 引言
多机器人协作策略是多机器人系统执行任务的前提,也是系统执行效率是否高效的关键,是组织简单机器人完成复杂任务的核心.尤其近几年云计算的兴起,任务分配的相关算法在云调度[1]中也发挥了重要的作用,因此具有重要的研究价值.
目前,多机器人协作策略研究主要集中于3种方法[2]:市场机制、群体智能和建模法.在动态环境中,多机器人系统经常面临任务在不确定的时间和不断变化的位置发布的问题[3].建模法最主要的优点就是实时性强,尤其在这种动态情况下,能较快地针对环境做出合理高效的决策.董炀斌等[4]创建的基于适应度的多机器人协作策略,在针对动态松散多任务分配方面展现了较好的实时性和灵活性,且能够在限制任务执行优先级、机器人能力有限[5]等情况下完成较优的任务分配,仿真试验表明,算法也具有较好的稳定性.冯晓海等[6]通过对该算法的改进,使用正余切函数作为外部适应度函数,避免了原始函数中一直归一化计算的问题,提高了机器人与任务之间适应度计算的稳定性.
1 适应度协作策略及其不足
1.1 外部适应度算法
外部能力适应度的计算如下:
(1)
外部能力适应度的归一化处理方法,
(2)
该算法很好地建立了任务的内部状态和外部联系,在机器人选择任务过程中,任务的内部状态即内部适应度保持不变,不会因为机器人的不同而改变.这也说明,机器人选择任务的关键在于它与任务的外部适应度,外部适应度的设置是否合理将直接影响到任务分配的效果.显然,外部适应度过度依赖全局信息且频繁进行归一化的过程增加了系统的复杂度,降低了稳定性.
1.2 正余切外部适应度算法
正余切外部适应度如下:
(3)
式中:Er为机器人的实际能力;Et为任务的实际需求能力.
改进的方法提高了算法的独立性,但也存在一些不合理:改进的外部适应度在较符合能力要求的范围内适应度值下降较快,在远超过能力的范围内适应度值保持较大值且下降缓慢.在计算适应度前,系统是有开关控制变量的,当机器人能力不足时,不进行适应度计算,它必须与其他机器人的能力进行加和、并操作后才能进行适应度的计算[7].在进行加和、并操作时,把能力不足时的适应度作为联合的依据不能保证联合的机器人组合与任务最优匹配,因此,对机器人能力不足时的外部适应度计算是多余的.
2 改进的外部适应度
2.1 改进外部能力适应度
在机器人能力满足任务需求时,计算能力适应度时,一般要求在较符合能力要求的范围内,能力适应度较大且区分明显;在远超出能力要求的范围内,能力适应度较小.为实现这一要求,笔者设计了基于高斯分布模型的外部能力适应度函数,如下式:
(4)
式中:L(i)为机器人Ri的实际能力水平;W(j)为任务Tj的实际能力需求.其仿真对比如图1、2.
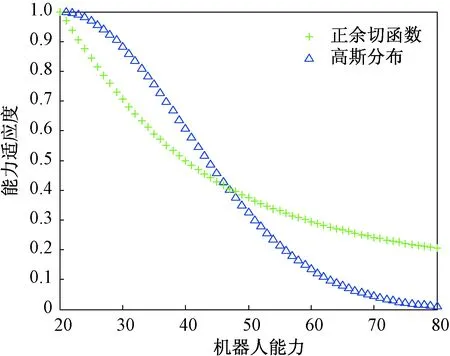
图1 W=20时的适应度值对比Fig.1 Fitness comparlson when W=20
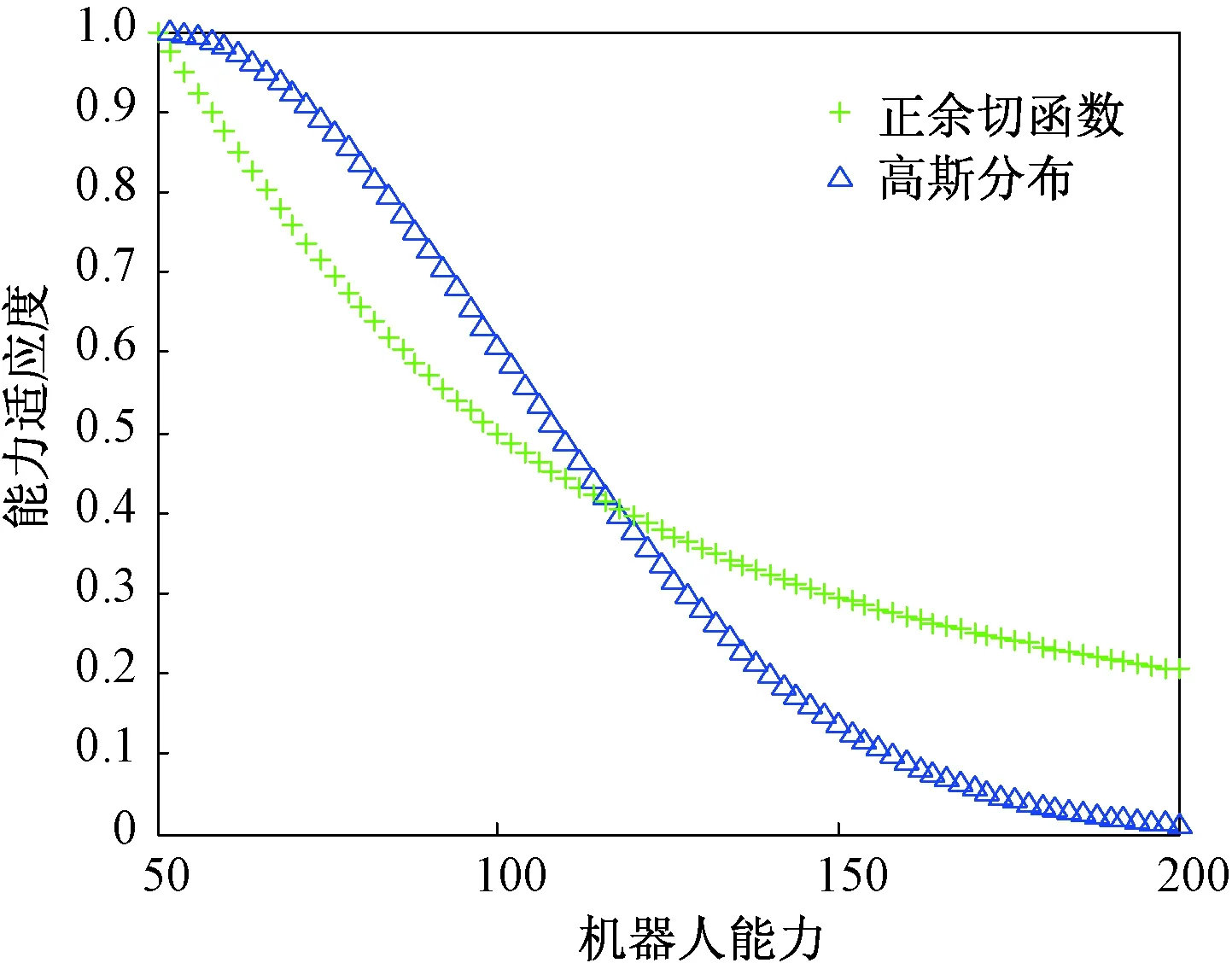
图2 W=50时的适应度值对比Fig.2 Fitness comparlson when W=50
从图1、2可以看出,在任务的能力需求是20(50)时,机器人在40(100)以内的适应度要比反余切函数的大,超过40(100)以后,适应度迅速减小,比反余切函数要小得多,可以保证其它能力在任务选择中占据主导,选择任务的匹配度更高.算法的计算只与该任务的能力需求和当前机器人的能力有关,不受系统里其它因素的影响,确保算法的独立性、稳定性和可延拓性.
2.2 距离适应度策略
图3为机器人不合理的任务选择.如图3所示,机器人起止位置异地,当A选择任务1后,B对1、2两个任务的适应度相同,按照原适应度算法的选择原则,由于1任务的编号在前,则机器人B将选择任务1,导致任务2漏选,从位置上看机器人B选择任务2更合理.显然,外部适应度如果只包含能力的匹配而不包含位置的匹配是不合理的,由此考虑加入机器人的代价[8].
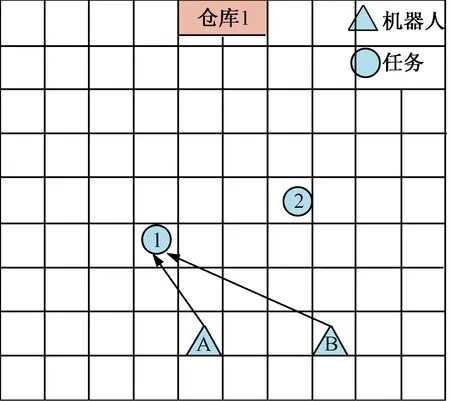
图3 机器人不合理的任务选择Fig.3 The unreasonable task selection of robots
基于此,笔者在外部适应度的结构中加入了与机器人起止位置有关的距离适应度函数,
(5)
式中:Fdis为距离适应度;Ldis为任务空间的最大距离,一般在任务之前就已经确定;RTdis(ij)为机器人Ri与任务Tj之间的距离.
外部适应度函数改为:
Aij=Wn·Nij+Wf·Fdisij,
(6)
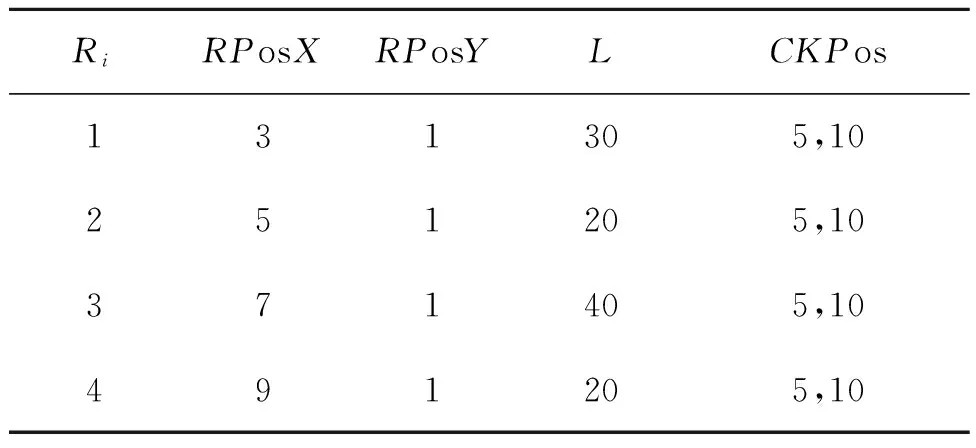
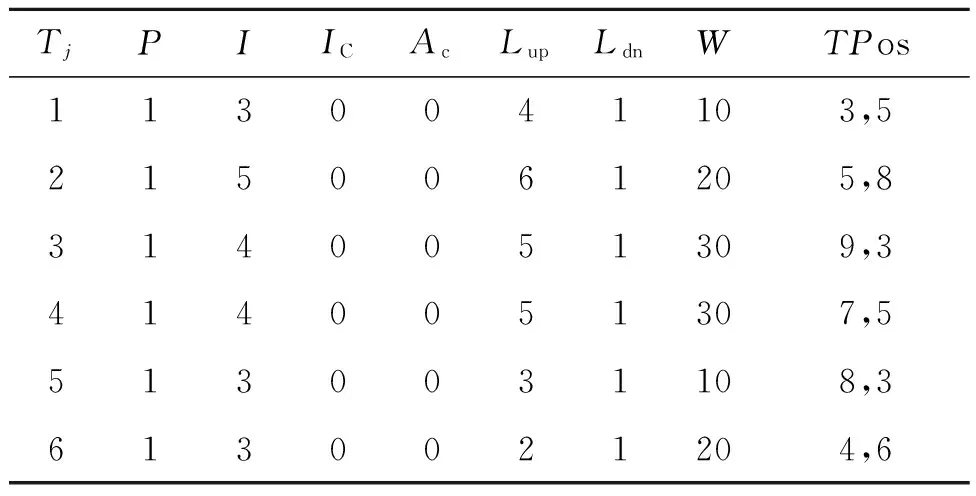
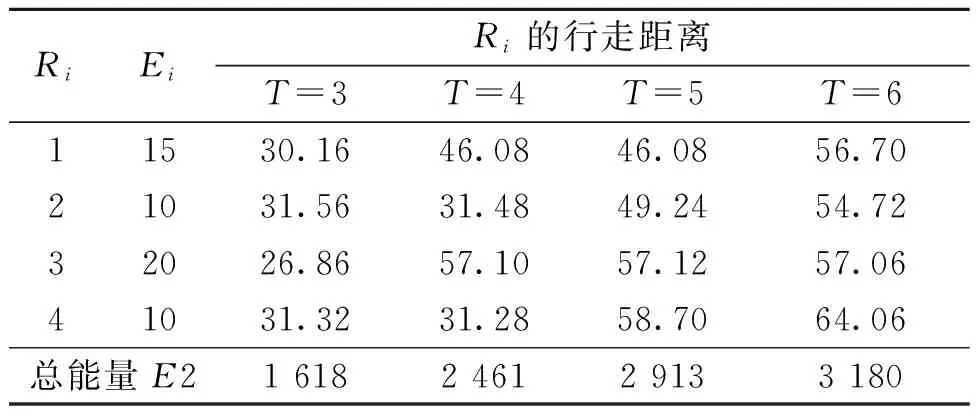
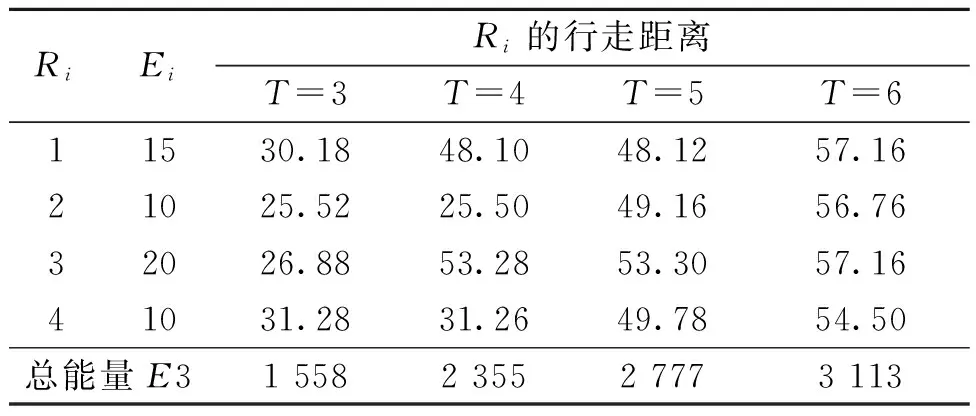
式中:Wn+Wf=1,0 任务分配中,不仅涉及到任务执行的时间效率,还要考虑机器人的能量消耗问题,只有这样才能保证任务是最优分配.为方便计算,给出多机器人执行任务的能量消耗计算公式, (7) Ei=Li/2, (8) 式中:E(i)为机器人Ri执行完所有任务的能量消耗;Ei为机器人Ri每行走1 m消耗的能量,与机器人的能力水平Li相关,机器人能力水平越大,则单位消耗的能量越大;LTij为机器人Ri执行任务Tj的行走路程. 改进后的算法与之前的算法相比有如下优点. ①改进后,针对图3中的问题,由于加入了距离适应度,使得机器人B对任务2的适应度更大,从而选择出了更合理且更优的任务. ②机器人起止位置异地.当机器人对任务的其他适应度相同时,机器人距离任务越近,则适应度越大.这样,机器人可以缩短一次返回行走的距离,节约时间.尤其是在大规模的任务分配中,将大大减少执行时间,如图4所示.图4中机器人A要将任务1、2送到仓库1.改进前A的任务执行顺序为:A→1→仓库1→2→仓库1,则机器人A的行程为21.59 m;改进后A的执行任务顺序为:A→2→仓库1→1→仓库1,机器人A的行程为18.10 m,缩短了行程. ③机器人起止位置相同.当机器人对任务的其他适应度相等时,距离越远的适应度越大.我们一般认为,当机器人与任务能力最匹配时达到资源的充分利用.因此,让最优匹配的机器人选择更远距离的任务,让过匹配的机器人去执行较近的,这样,在总行走距离相等的情况下,总体节约了能量.如图4,让机器人B、C分别将任务1、2送到仓库1.其中,B对两任务的适应度相同且属于最优匹配,C对两任务是属于过匹配.改进前分配结果为:B→1,C→2;改进后分配结果为:B→2,C→1.根据公式(7)计算可知改进后更节省能量,证明如下. 已知:0 改进前的能量消耗: E(B)=L(B)/2·LT1,E(C)=L(C)/2·LT2, E1=L(B)/2·LT1+L(C)/2·LT2. 改进后的能量消耗: E(B)=L(B)/2·LT2,E(C)=L(C)/2·LT1, E2=L(B)/2·LT2+L(C)/2·LT1. ΔE=E1-E2 =L(B)/2·LT1+L(C)/2·LT2- (L(B)/2·LT2+L(C)/2·LT1)= (L(B)-L(C))(LT1-LT2)/2>0. 证毕. 图4 机器人和任务分布图Fig.4 The distribution of robots and tasks 以搬运任务进行验证,在一个10×10 m的空间内,配备有4个机器人,为进行对比仿真验证,每个机器人的能力水平各不相同,机器人起始位置也不相同,任务的能力需求、位置、数量也各不相同,在执行任务期间,机器人均以0.24 m/s的速度行进,仿真试验分别对不同组合的任务进行分配和结果分析. 表1是机器人的初始参数,其中,Ri是机器人编号;RPosX、RPosY是机器人坐标;L是机器人能力水平;CKPos是仓库位置.表2是任务的一些初始参数,Tj是任务编号;P是任务优先级;I是子任务总量;Ic是子任务完成量;Ar是当前选择本子任务的机器人数;Lup是允许机器人上限[9];Ldn是允许机器人下限;W是任务能力需求;TPos是任务坐标.初始时,起止位置异地.内部适应度参数设置为Ws=0,Wp=0.8,Wr=0.2,第一次任务选择时,要保证机器人尽量选择较近的任务,参数设置为:Wn=0.2,Wf=0.8,接下来的参数设置为Wn=0.5,Wf=0.5. 表1 机器人初始参数 表2 任务初始参数 针对此次试验,我们假设不考虑机器人之间的避碰耗时,机器人在执行任务中能力保持不变,机器人依次进行任务选择.为了保证试验的可靠性和严谨性,笔者特意设计了没有适应度相同的情况和有两个任务适应度相同位置不同的情况,这两个任务分别是任务3和4.试验分别以任务组合(1、2、3),(1、2、3、4),(1、2、3、4、5),(1、2、3、4、5、6)进行4组仿真试验.为了验证试验的有效性,试验还分别用原始适应度算法、正余切改进的适应度算法进行了仿真试验验证,试验结果如表3. 表3 执行任务时间对比 从表3可以看出,T=3时,任务中没有适应度相同的任务,原始适应度算法比正余切改进的算法、笔者改进的算法运行时间都要长;当T=4 ~6时,任务中有一组会出现刚开始适应度相同的情况,此时笔者改进的算法运行时间明显小于原始算法和正余切改进的算法,说明改进的算法有效且效率更高. 根据仿真试验,可以得到每个机器人的行走距离及能力大小,然后通过公式(7)可以计算出所有任务执行结束后每个机器人的总能量消耗,3种方法的统计结果如表4~6所示. 由以上3组的能量计算可看出,笔者改进的算法能量消耗最低,即使在T=3时,正余切改进的算法和笔者算法执行时间相差无几,但能量消耗却大于笔者改进的算法,由此证明笔者改进的算法也实现了能量的消耗最低. 表4 原算法的能量消耗 表5 正余切算法的能量消耗 表6 笔者改进算法的能量消耗 主要研究了基于改进适应度的多机器人协作策略,针对适应度算法的外部能力匹配度不够理想的问题,提出了高斯分布模型来计算机器人的能力匹配度.仿真表明,笔者算法更符合匹配度的要求,且保证了算法的独立性与延拓性.针对出现适应度相同的任务时,机器人可能无法选择出最合理任务的问题,通过加入与机器人起止位置有关的距离适应度,不仅解决了适应度相同时依次分配带来的不合理,提高了算法分配合理性,而且任务的执行效率也明显提升,保证能量消耗最低,在松散多机器人环境中,该算法优于改进前的算法. 参考文献: [1]王俊英,颜芬芬. 基于概率自适应蚁群算法的云任务调度方法[J]. 郑州大学学报(工学版),2017,38(4):51-56. [2]张嵛,刘淑华. 多机器人任务分配的研究进展[J]. 智能系统学报,2008,3(2):115-120. [3]CHEN Y, MAO X J,HOU F,et al. Combining re-allocating and re-scheduling for dynamic multi-robot task allocation [C]∥IEEE Intermational Conference on Systems,Man,and Cybernetics.Budapest:IEEE,2016:000395-000400. [4]董炀斌,蒋静坪. 基于适应度的多机器人任务分配策略[J]. 浙江大学学报(工学版),2007,41(2):272-277. [5]MITICHE H, BOUGHACI D,GINI M.Efficient heuristics for a time-extended multi-robot task allocation problem [C]∥International Conference on New Technologies of Information & Communication, 2015:1-6. [6]张万绪,冯晓海,赵江波,等. 改进适应度的异构多机器人任务分配[J]. 西北工业大学(自然科学版),2013,43(1):22-26. [7]柳林,季秀才,郑志强. 基于市场法及能力分类的多机器人任务分配方法[J]. 机器人,2006,28(3):337-343. [8]韦兆文,区云鹏,闫俊燕. 一种改进的动态合同网协议[J].计算机工程与应用,2007,43(36):208-211. [9]LERMAN K, GALSTYAN A. A general methodology for mathematical analysis of multi-agent systems [R]. Los Angeles:USC information sciences technical report ISI-TR-529,2001.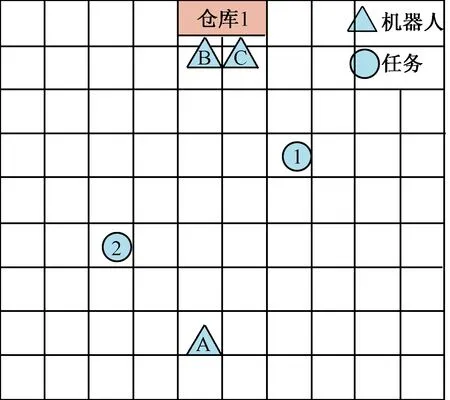
3 仿真试验


4 结论

